Big Data

Coeficiente de correlación de Pearson: una guía para principiantes

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Introducción

Considere el ejemplo de detección del precio del automóvil donde tenemos que detectar el precio considerando todas las variables que afectan el precio del automóvil, como la longitud del automóvil, el peso en vacío, la altura del automóvil, el ancho del automóvil, el tipo de combustible, la carrocería, la potencia, etc.

Se puede encontrar correlación entre variables continuas usando Python:

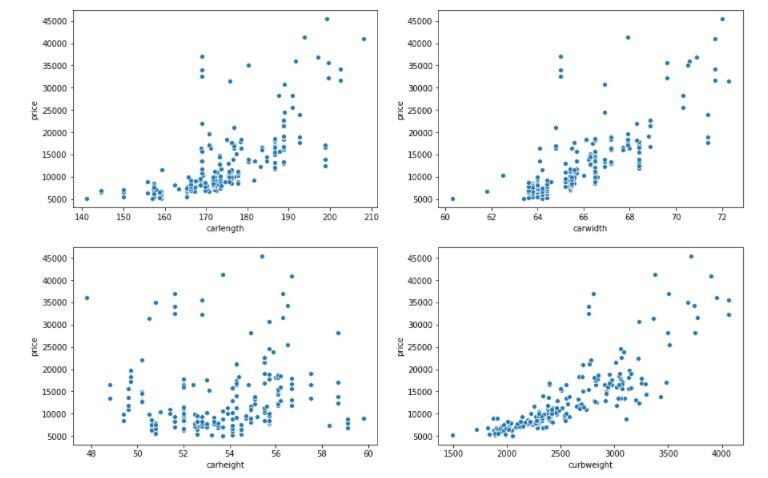
Podemos ver en el diagrama de dispersiónEl diagrama de dispersión es una herramienta gráfica utilizada en estadística para visualizar la relación entre dos variables. Consiste en un conjunto de puntos en un plano cartesiano, donde cada punto representa un par de valores correspondientes a las variables analizadas. Este tipo de gráfico permite identificar patrones, tendencias y posibles correlaciones, facilitando la interpretación de datos y la toma de decisiones basadas en la información visual presentada.... anterior, ya que la longitud del automóvil, el peso en vacío y el ancho del automóvil aumentan, el precio del automóvil también aumenta. Entonces, podemos decir que existe una correlación positiva entre las tres variables anteriores con el precio del automóvil. Aquí, también vemos que no existe una correlación entre la altura del automóvil y el precio del automóvil.

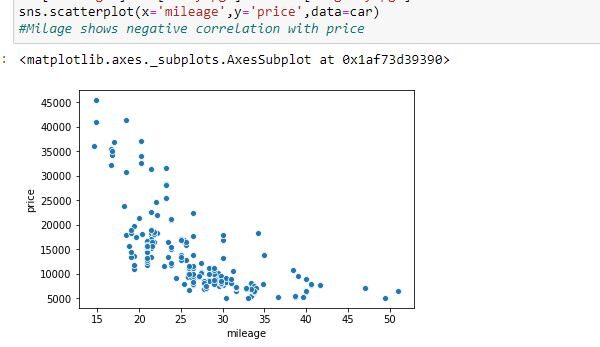
Los coches con precios elevados tienen un kilometraje muy reducido en comparación con los coches de gama baja. Por tanto, en este caso, podemos decir que existe una correlación negativa entre el precio del coche y el kilometraje.

Definición

Centrémonos en una explicación estadística del mismo. El coeficiente de correlación de Pearson se representa como ‘r’, mide qué tan fuerte es la asociación lineal entre dos variables continuas usando la fórmula:

Los valores de la correlación de Pearson son:

El valor de ‘r’ varía de ‘-1’ a ‘+1’. El valor ‘0’ especifica que no hay relación entre las dos variables. Un valor mayor que ‘0’ indica una relación positiva entre dos variables donde un aumento en el valor de una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aumenta el valor de otra variable. Un valor menor que ‘0’ indica una relación negativa entre dos variables donde un aumento en el valor de una disminuye el valor de otra variable.

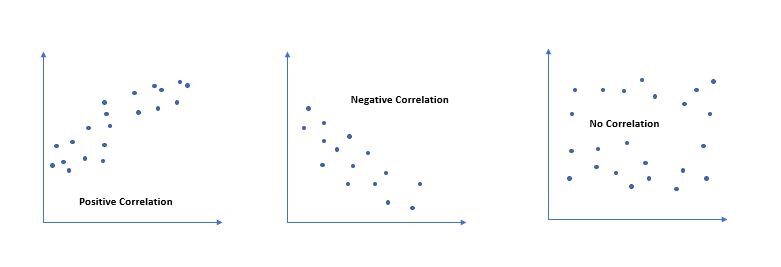
La correlación de Pearson intenta trazar una línea de mejor ajuste a través de la dispersión de dos variables. Por lo tanto, especifica qué tan lejos están todos estos puntos de datos de la línea de mejor ajuste. Valor de ‘r’ igual a cerca de +1 o -1, lo que significa que todos los puntos de datos se incluyen en o cerca de la línea de mejor ajuste, respectivamente. El valor de ‘r’ más cercano a los puntos de datos ‘0’ está alrededor de la línea de mejor ajuste.

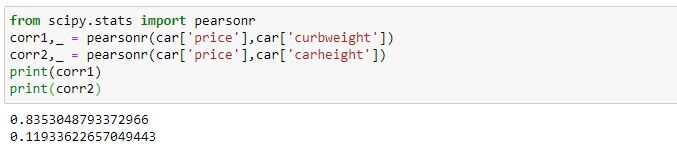
Considerando el mismo ejemplo del precio del automóvil, averigüemos el valor ‘r’ usando la función ‘pearsonr’ en Python.

Como se indicó anteriormente, el valor de la correlación de Pearson para el precio frente al peso en vacío es 0,835 y, como no hay correlación entre el precio y la altura del automóvil, el valor de la correlación de Pearson entre el precio y la altura del automóvil está cerca de 0, que es 0,12.

Supuestos para una correlación de Pearson:

1. Los datos deben derivarse de muestras aleatorias o menos representativas, extraer una inferencia estadística significativa.

2. Ambas variables deben ser continuas y estar distribuidas normalmente.

3. Debe haber homocedasticidad, lo que significa que la variación alrededor de la línea de mejor ajuste debe ser similar.

4. Los valores atípicos extremos influyen en el coeficiente de correlación de Pearson. Debe considerar los valores atípicos que son inusuales solo en una variable, denominada ‘variable univariante’ o para ambas variables conocidas como ‘valores atípicos multivariados’. Se miden 2 variables independientemente entre sí. Por ejemplo, si graficamos la edad frente al monto, entonces, ciertamente podemos ver que existe una correlación entre la edad de una persona y el préstamo, el monto se le otorga a esa persona, a medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que la edad aumenta el monto del préstamo otorgado a la persona.

persona disminuye y viceversa. Pero si graficamos el monto del préstamo en función de la edad, no es posible extraer ninguna conclusión. Violaría la suposición.