Este artículo fue publicado como parte del Blogatón de ciencia de datos
Introducción
En mi artículo anterior, hablo sobre los conceptos teóricos sobre los valores atípicos y trato de encontrar la respuesta a la pregunta: «¿Cuándo tenemos que eliminar los valores atípicos y cuándo mantener los valores atípicos?».
Para comprender mejor este artículo, primero debe leer que artículo y luego continúe con esto para que tenga una idea clara sobre el análisis de valores atípicos en Proyectos de ciencia de datos.
En este artículo, intentaremos dar respuesta a las siguientes preguntas junto con la Pitón implementación,
👉 ¿Cómo tratar los valores atípicos?
👉 ¿Cómo detectar valores atípicos?
👉 ¿Cuáles son las técnicas para la detección y eliminación de valores atípicos?
Empecemos
¿Cómo tratar los valores atípicos?
👉 Guarnición: Excluye los valores atípicos. de nuestro análisis. Aplicando esta técnica nuestro los datos se vuelven delgados cuando hay más valores atípicos presentes en el conjunto de datos. Su principal ventaja es su lo más rápido naturaleza.
👉Taponamiento: En esta técnica, Cap nuestro datos atípicos y haga el límite es decir, por encima de un valor particular o por debajo de ese valor, todos los valores se considerarán valores atípicos, y el número de valores atípicos en el conjunto de datos da ese número de límite.
Por ejemplo, Si está trabajando en la función de ingresos, es posible que las personas que superen un cierto nivel de ingresos se comporten de la misma manera que las que tienen ingresos más bajos. En este caso, puede limitar el valor de los ingresos a un nivel que lo mantenga intacto y, en consecuencia, tratar los valores atípicos.
👉Trate los valores atípicos como un valor faltante: Por suponiendo valores atípicos como las observaciones faltantes, trátelos en consecuencia, es decir, iguales a los valores faltantes.
Puede consultar el artículo de valor faltante aquí
👉 Discretización: En esta técnica, al hacer los grupos incluimos los valores atípicos en un grupo en particular y los obligamos a comportarse de la misma manera que los de otros puntos de ese grupo. Esta técnica también se conoce como Binning.
Puedes aprender más sobre discretización aquí.
¿Cómo detectar valores atípicos?
👉 Para distribuciones normales: Utilice relaciones empíricas de distribución normal.
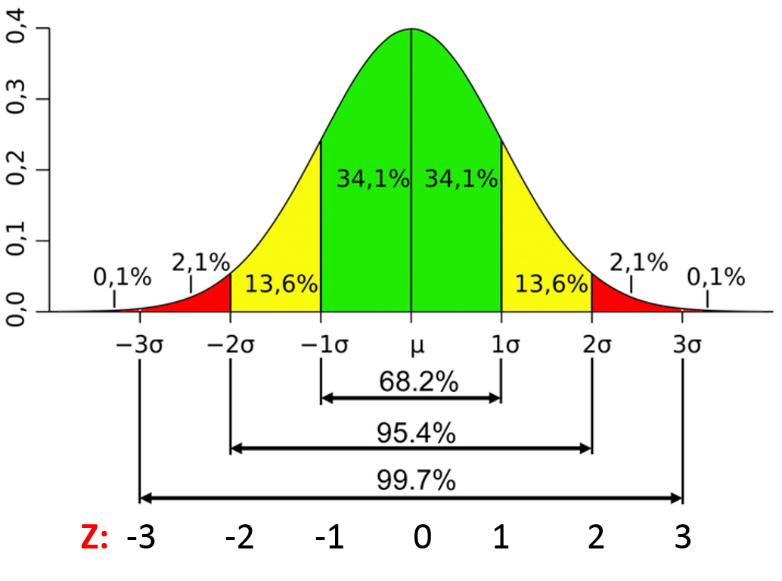
– Los puntos de datos que se encuentran debajo media-3 * (sigma) o por encima media + 3 * (sigma) son valores atípicos.
donde mean y sigma son los valor promedio y Desviación Estándar de una columna en particular.
Fig. Características de una distribución normal
Fuente de imagen: Enlace
👉 Para distribuciones sesgadas: Utilice la regla de proximidad Inter-Quartile Range (IQR).
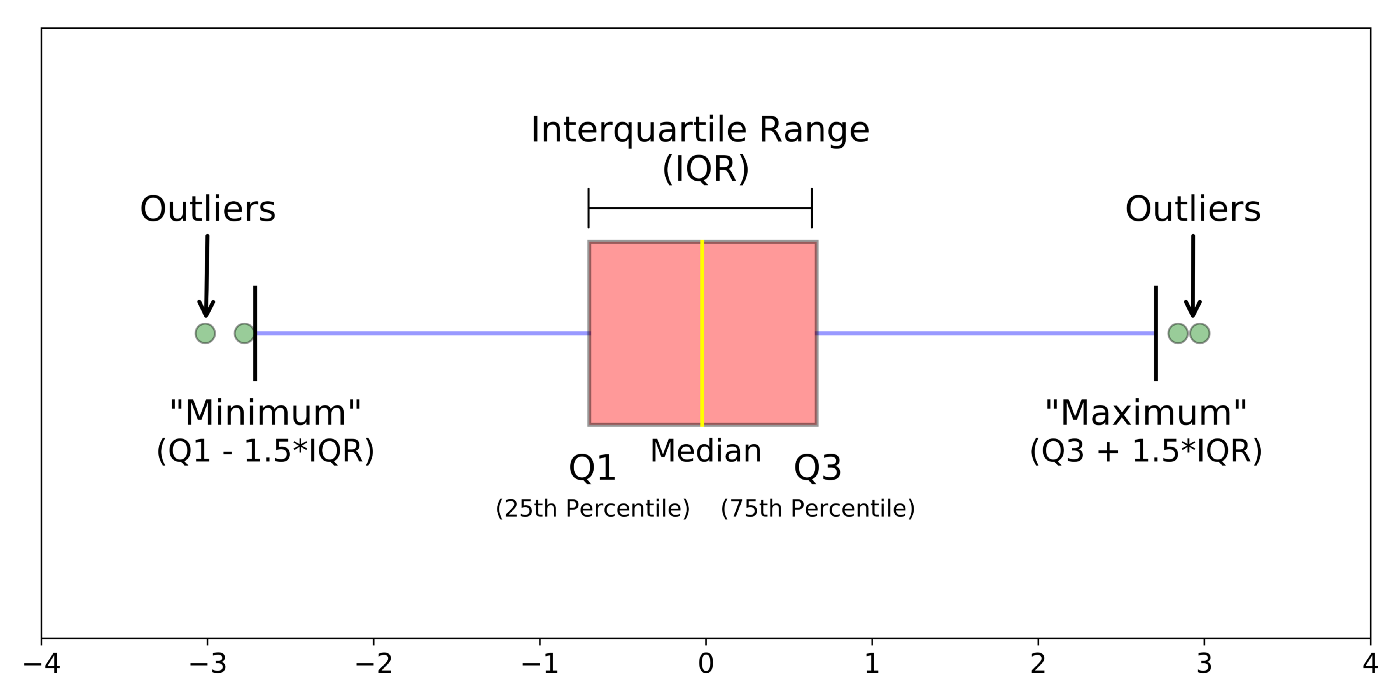
– Los puntos de datos que se encuentran debajo Q1 – 1.5 IQR o por encima Q3 + 1.5 IQR son valores atípicos.
donde Q1 y Q3 son los 25 y Percentil 75 del conjunto de datos respectivamente, y IQR representa el rango intercuartil y está dado por Q3 – Q1.
Fig. IQR para detectar valores atípicos
Fuente de imagen: Enlace
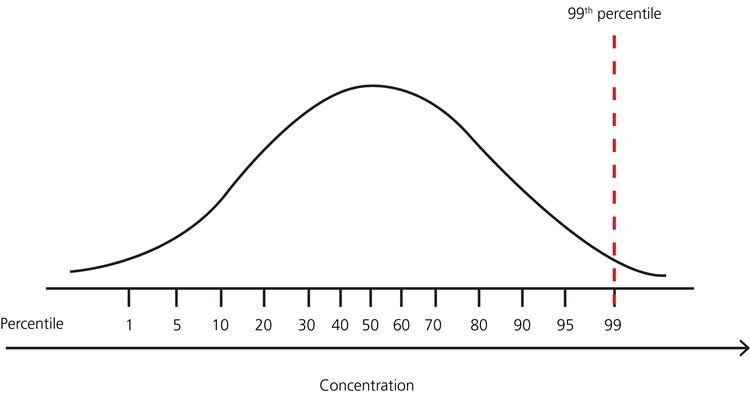
👉 Para otras distribuciones: Usar enfoque basado en percentiles.
Por ejemplo, Los puntos de datos que están lejos del percentil 99% y menos del percentil 1 se consideran valores atípicos.
Fig. Representación percentil
Fuente de imagen: Enlace
Técnicas para la detección y eliminación de valores atípicos:
👉 Tratamiento de puntuación Z:
Suposición– Las características están distribuidas normal o aproximadamente normalmente.
Paso 1: Importación de las dependencias necesarias
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns
Paso 2: leer y cargar el conjunto de datos
df = pd.read_csv('placement.csv')
df.sample(5)
Paso 3: Trace las gráficas de distribución para las características
import warnings
warnings.filterwarnings('ignore')
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
sns.distplot(df['cgpa'])
plt.subplot(1,2,2)
sns.distplot(df['placement_exam_marks'])
plt.show()
Paso 4: encontrar los valores límite
print("Highest allowed",df['cgpa'].mean() + 3*df['cgpa'].std())
print("Lowest allowed",df['cgpa'].mean() - 3*df['cgpa'].std())Producción:
Highest allowed 8.808933625397177 Lowest allowed 5.113546374602842
Paso 5: encontrar los valores atípicos
df[(df['cgpa'] > 8.80) | (df['cgpa'] < 5.11)]
Paso 6: Recorte de valores atípicos
new_df = df[(df['cgpa'] < 8.80) & (df['cgpa'] > 5.11)] new_df
Paso 7: limitación de valores atípicos
upper_limit = df['cgpa'].mean() + 3*df['cgpa'].std() lower_limit = df['cgpa'].mean() - 3*df['cgpa'].std()
Paso 8: ahora, aplique la tapa
df['cgpa'] = np.where(
df['cgpa']>upper_limit,
upper_limit,
np.where(
df['cgpa']<lower_limit,
lower_limit,
df['cgpa']
)
)Paso 9: ahora vea las estadísticas usando la función «Describir»
df['cgpa'].describe()
Producción:
count 1000.000000 mean 6.961499 std 0.612688 min 5.113546 25% 6.550000 50% 6.960000 75% 7.370000 max 8.808934 Name: cgpa, dtype: float64
¡Esto completa nuestra técnica basada en puntaje Z!
👉 Filtrado basado en IQR:
Se usa cuando nuestra distribución de datos está sesgada.
Paso 1: importar las dependencias necesarias
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns
Paso 2: leer y cargar el conjunto de datos
df = pd.read_csv('placement.csv')
df.head()Paso 3: Trace la gráfica de distribución de las características.
plt.figure(figsize=(16,5)) plt.subplot(1,2,1) sns.distplot(df['cgpa']) plt.subplot(1,2,2) sns.distplot(df['placement_exam_marks']) plt.show()
Paso 4: Forme un diagrama de caja para la característica sesgada
sns.boxplot(df['placement_exam_marks'])
Paso 5: Encontrar el IQR
percentile25 = df['placement_exam_marks'].quantile(0.25) percentile75 = df['placement_exam_marks'].quantile(0.75)
Paso 6: Encontrar el límite superior e inferior
upper_limit = percentile75 + 1.5 * iqr lower_limit = percentile25 - 1.5 * iqr
Paso 7: encontrar valores atípicos
df[df['placement_exam_marks'] > upper_limit] df[df['placement_exam_marks'] < lower_limit]
Paso 8: Recorte
new_df = df[df['placement_exam_marks'] < upper_limit] new_df.shape
Paso 9: Compare las parcelas después de recortar
plt.figure(figsize=(16,8)) plt.subplot(2,2,1) sns.distplot(df['placement_exam_marks']) plt.subplot(2,2,2) sns.boxplot(df['placement_exam_marks']) plt.subplot(2,2,3) sns.distplot(new_df['placement_exam_marks']) plt.subplot(2,2,4) sns.boxplot(new_df['placement_exam_marks']) plt.show()
Paso 10: taponado
new_df_cap = df.copy()
new_df_cap['placement_exam_marks'] = np.where(
new_df_cap['placement_exam_marks'] > upper_limit,
upper_limit,
np.where(
new_df_cap['placement_exam_marks'] < lower_limit,
lower_limit,
new_df_cap['placement_exam_marks']
)
)Paso 11: Compare las parcelas después de la limitación
plt.figure(figsize=(16,8)) plt.subplot(2,2,1) sns.distplot(df['placement_exam_marks']) plt.subplot(2,2,2) sns.boxplot(df['placement_exam_marks']) plt.subplot(2,2,3) sns.distplot(new_df_cap['placement_exam_marks']) plt.subplot(2,2,4) sns.boxplot(new_df_cap['placement_exam_marks']) plt.show()
¡Esto completa nuestra técnica basada en IQR!
👉 Percentil:
– Esta técnica funciona estableciendo un valor de umbral particular, que decide en función de nuestro planteamiento del problema.
– Si bien eliminamos los valores atípicos mediante la limitación, ese método en particular se conoce como Winsorización.
– Aquí siempre mantenemos simetría en ambos lados significa que si eliminamos el 1% de la derecha, entonces en la izquierda también disminuimos un 1%.
Paso 1: importar las dependencias necesarias
import numpy as np import pandas as pd
Paso 2: leer y cargar el conjunto de datos
df = pd.read_csv('weight-height.csv')
df.sample(5)
Paso 3: Trace la gráfica de distribución de la característica de «altura»
sns.distplot(df['Height'])
Paso 4: Trace el diagrama de caja de la característica de «altura»
sns.boxplot(df['Height'])
Paso 5: Encontrar el límite superior e inferior
upper_limit = df['Height'].quantile(0.99) lower_limit = df['Height'].quantile(0.01)
Paso 7: aplique el recorte
new_df = df[(df['Height'] <= 74.78) & (df['Height'] >= 58.13)]
Paso 8: Compare la distribución y el diagrama de caja después de recortar
sns.distplot(new_df['Height']) sns.boxplot(new_df['Height'])
👉 Winsorización:
Paso 9: Aplicar limitación (Winsorización)
df['Height'] = np.where(df['Height'] >= upper_limit,
upper_limit,
np.where(df['Height'] <= lower_limit,
lower_limit,
df['Height']))Paso 10: Compare la distribución y el diagrama de caja después de la limitación
sns.distplot(df['Height']) sns.boxplot(df['Height'])
¡Esto completa nuestra técnica basada en percentiles!
Notas finales
¡Gracias por leer!
Si le gustó esto y quiere saber más, visite mis otros artículos sobre ciencia de datos y aprendizaje automático haciendo clic en el Enlace
No dude en ponerse en contacto conmigo en Linkedin, Correo electrónico.
¿Algo no mencionado o quieres compartir tus pensamientos? No dude en comentar a continuación y me pondré en contacto con usted.
Sobre el Autor
Chirag Goyal
Actualmente, estoy cursando mi Licenciatura en Tecnología (B.Tech) en Ciencias de la Computación e Ingeniería de la Instituto Indio de Tecnología de Jodhpur (IITJ). Estoy muy entusiasmado con el aprendizaje automático, el aprendizaje profundo y la inteligencia artificial.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.
