Este artículo fue publicado como parte del Blogatón de ciencia de datos
Agenda
Todos hemos construido una regresión logística en algún momento de nuestras vidas. Incluso si nunca hemos construido un modelo, definitivamente hemos aprendido teóricamente esta técnica de modelo predictivo. Dos conceptos simples y infravalorados que se utilizan en el paso de preprocesamiento para construir un modelo de regresión logística son el peso de la evidencia y el valor de la información. Me gustaría traerlos de vuelta al centro de atención a través de este artículo.
Este artículo está estructurado de la siguiente manera:
- Introducción a la regresión logística
- Importancia de la selección de características
- Necesidad de un buen imputador para características categóricas
- AFLICCIÓN
- IV
¡Empecemos!
1. Introducción a la regresión logística
Lo primero es lo primero, todos sabemos que la regresión logística es un problema de clasificación. En particular, consideramos aquí los problemas de clasificación binaria.
Los modelos de regresión logística toman como entrada tanto datos categóricos como numéricos y dan salida a la probabilidad de ocurrencia del evento.
Ejemplos de enunciados de problemas que se pueden resolver con este método son:
- Dados los datos del cliente, ¿cuál es la probabilidad de que el cliente compre un nuevo producto presentado por una empresa?
- Dados los datos requeridos, ¿cuál es la probabilidad de que un cliente bancario no pague un préstamo?
- Dados los datos meteorológicos del último mes, ¿cuál es la probabilidad de que llueva mañana?
Todas las declaraciones anteriores tuvieron dos resultados. (comprar y no comprar, predeterminado y no predeterminado, lluvia y no lluvia). Por tanto, se puede construir un modelo de regresión logística binaria. La regresión logística es un método paramétrico. ¿Qué significa esto? Un método paramétrico tiene dos pasos.
1. Primero, asumimos una forma o forma funcional. En el caso de la regresión logística, asumimos que

2. Necesitamos predecir los pesos / coeficientes bi de manera que, la probabilidad de un evento para una observación x sea cercana a 1 si el valor real del objetivo es 1 y la probabilidad es cercana a 0 si el valor real del objetivo es 0.
Con esta comprensión básica, comprendamos por qué necesitamos la selección de funciones.
2. Importancia de la selección de características
En esta era digital, estamos equipados con una enorme cantidad de datos. Sin embargo, no todas las funciones disponibles para nosotros son útiles en todas las predicciones del modelo. Todos hemos escuchado el dicho “¡Entra basura, sale basura!”. Por lo tanto, elegir las características adecuadas para nuestro modelo es de suma importancia. Las funciones se seleccionan en función de la fuerza predictiva de la función.
Por ejemplo, digamos que queremos predecir la probabilidad de que una persona compre una nueva receta de pollo en nuestro restaurante. Si tenemos una función: «Preferencia de comida» con valores {Vegetariano, No vegetariano, Eggetariano}, estamos casi seguros de que esta función separará claramente a las personas que tienen una mayor probabilidad de comprar este nuevo plato de las que nunca lo comprarán. . Por lo tanto, esta característica tiene un alto poder predictivo.
Podemos cuantificar el poder predictivo de una característica utilizando el concepto de valor de la información que se describirá aquí.
3. Necesidad de un buen imputador para funciones categóricas
La regresión logística es un método paramétrico que requiere que calculemos una ecuación lineal. Esto requiere que todas las características sean numéricas. Sin embargo, es posible que tengamos características categóricas en nuestros conjuntos de datos que sean nominales u ordinales. Hay muchos métodos de imputación como la codificación one-hot o simplemente asignar un número a cada clase de características categóricas. cada uno de estos métodos tiene sus propios méritos y deméritos. Sin embargo, no discutiré lo mismo aquí.
En el caso de la regresión logística, podemos utilizar el concepto WoE (Weight of Evidence) para imputar las características categóricas.
4. Peso de las pruebas
Después de todos los antecedentes proporcionados, ¡finalmente hemos llegado al tema del día!
La fórmula para calcular el peso de la evidencia para cualquier característica viene dada por
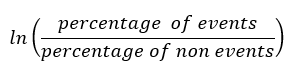
Antes de continuar explicando la intuición detrás de esta fórmula, tomemos un ejemplo ficticio:
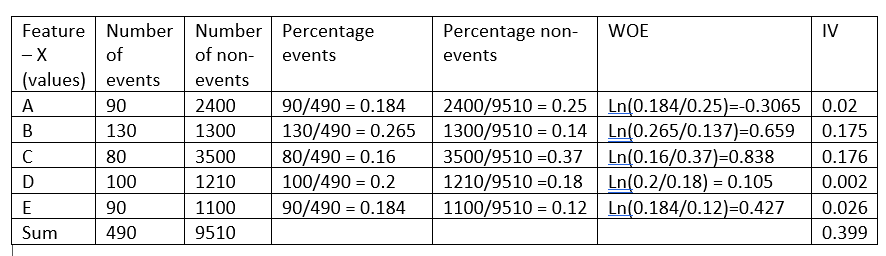
El peso de la evidencia indica el poder predictivo de una sola característica con respecto a su característica independiente. Si alguna de las categorías / bins de una característica tiene una gran proporción de eventos en comparación con la proporción de no eventos, obtendremos un valor alto de WoE que a su vez dice que esa clase de característica separa los eventos de los no eventos. .
Por ejemplo, considere la categoría C de la característica X en el ejemplo anterior, la proporción de eventos (0,16) es muy pequeña en comparación con la proporción de no eventos (0,37). Esto implica que si el valor de la característica X es C, es más probable que el valor objetivo sea 0 (sin evento). El valor WoE solo nos dice qué tan seguros estamos de que la función nos ayudará a predecir correctamente la probabilidad de un evento.
Ahora que sabemos que WoE mide el poder predictivo de cada bin / categoría de una característica, ¿cuáles son los otros beneficios de WoE?
1. Los valores de WoE para las diversas categorías de una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... categórica se pueden utilizar para imputar una característica categórica y convertirla en una característica numérica, ya que un modelo de regresión logística requiere que todas sus características sean numéricas.
Al examinar cuidadosamente la fórmula de WoE y la ecuación de regresión logística a resolver, vemos que WoE de una característica tiene una relación lineal con las probabilidades logarítmicas. Esto asegura que se satisfaga el requisito de que las características tengan una relación lineal con las probabilidades logarítmicas.
2. Por la misma razón que la anterior, si una característica continua no tiene una relación lineal con las probabilidades de registro, la característica se puede agrupar en grupos y se puede usar una nueva característica creada reemplazando cada contenedor con su valor WoE en lugar de la característica original. Por tanto, WoE es un buen método de transformación de variables para la regresión logística.
3. Al organizar una característica numérica en orden ascendente, si los valores de WoE son todos lineales, sabemos que la característica tiene la relación lineal correcta con el objetivo. Sin embargo, si la WoE de la característica no es lineal, debemos descartarla o considere alguna otra transformación de variable para asegurar la linealidad. Por lo tanto, WoE nos brinda una herramienta para verificar la relación lineal con la característica dependiente.
4. WoE es mejor que la codificación one-hot ya que la codificación one-hot necesitará que cree nuevas características h-1 para acomodar una característica categórica con categorías h. Esto implica que el modelo no tendrá que predecir coeficientes h-1 (bi) en lugar de 1. Sin embargo, en la transformación de la variable WoE, necesitaremos calcular un coeficiente único para la característica en consideración.
5. Valor de la información
Habiendo discutido el valor WoE, el valor WoE nos dice el poder predictivo de cada bin de una característica. Sin embargo, un solo valor que represente el poder predictivo de toda la característica será útil en la selección de características.
La ecuación para IV es
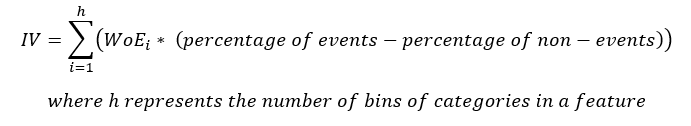
Tenga en cuenta que el término (porcentaje de eventos – el porcentaje de no eventos) sigue el mismo signo que WoE, por lo tanto, se asegura de que el IV sea siempre un número positivo.
¿Cómo interpretamos el valor de IV?
La siguiente tabla le brinda una regla fija para ayudarlo a seleccionar las mejores características para su modelo
| Valor de la información | Poder de predicción |
| <0.02 | Inútil |
| 0,02 hasta 0,1 | Predictores débiles |
| 0,1 hasta 0,3 | Predictores medios |
| 0,3 hasta 0,5 | Fuertes predictores |
| > 0,5 | Suspicaz |
Como se ve en el ejemplo anterior, la característica X tiene un valor de información de 0.399, lo que la convierte en un predictor sólido y, por lo tanto, se utilizará en el modelo.
6. Conclusión
Como se ve en el ejemplo anterior, el cálculo del WoE y el IV son beneficiosos y nos ayudan a analizar múltiples puntos como se enumeran a continuación.
1. WoE ayuda a verificar la relación lineal de una característica con su característica dependiente que se utilizará en el modelo.
2. WoE es un buen método de transformación de variables para características continuas y categóricas.
3. WoE es mejor que la codificación en caliente, ya que este método de transformación de variables no aumenta la complejidad del modelo.
4. IV es una buena medida del poder predictivo de una característica y también ayuda a señalar la característica sospechosa.
Aunque WoE y IV son muy útiles, asegúrese siempre de que solo se utilice con regresión logística. A diferencia de otros métodos de selección de características disponibles, las características seleccionadas mediante IV pueden no ser el mejor conjunto de características para una construcción de modelos no lineales.
Espero que este artículo te haya ayudado a intuir el funcionamiento de WoE y IV.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






