Introducción
La red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... es una máquina de procesamiento de información y puede considerarse análoga al sistema nervioso humano. Al igual que el sistema nervioso humano, que está formado por neuronas interconectadas, una red neuronal está formada por unidades de procesamiento de información interconectadas. Las unidades de procesamiento de información no funcionan de manera lineal. De hecho, la red neuronal obtiene su fuerza del procesamiento paralelo de información, lo que le permite lidiar con la no linealidad. La red neuronal se vuelve útil para inferir significados y detectar patrones a partir de conjuntos de datos complejos.
La red neuronal está considerada como una de las técnicas más útiles en el mundo de la analíticaLa analítica se refiere al proceso de recopilar, medir y analizar datos para obtener información valiosa que facilite la toma de decisiones. En diversos campos, como los negocios, la salud y el deporte, la analítica permite identificar patrones y tendencias, optimizar procesos y mejorar resultados. El uso de herramientas avanzadas y técnicas estadísticas es fundamental para transformar datos en conocimiento aplicable y estratégico.... de datos. Sin embargo, es complejo y a menudo se lo considera una caja negra, es decir, los usuarios ven la entrada y la salida de una red neuronal pero no tienen ni idea del proceso de generación de conocimiento. Esperamos que el artículo ayude a los lectores a aprender sobre el mecanismo interno de una red neuronal y a adquirir experiencia práctica para implementarlo en R.
Tabla de contenido
- Los fundamentos de la red neuronal
- Ajuste de la red neuronal en R
- Validación cruzada de una red neuronal
Los fundamentos de la red neuronal
Una red neuronal es un modelo caracterizado por una función de activaciónLa función de activación es un componente clave en las redes neuronales, ya que determina la salida de una neurona en función de su entrada. Su propósito principal es introducir no linealidades en el modelo, permitiendo que aprenda patrones complejos en los datos. Existen diversas funciones de activación, como la sigmoide, ReLU y tanh, cada una con características particulares que afectan el rendimiento del modelo en diferentes aplicaciones...., que es utilizada por unidades de procesamiento de información interconectadas para transformar la entrada en salida. Una red neuronal siempre se ha comparado con el sistema nervioso humano. La información pasa a través de unidades interconectadas de forma análoga al paso de información a través de las neuronas en los seres humanos. La primera capa de la red neuronal recibe la entrada sin procesar, la procesa y pasa la información procesada a las capas ocultas. La capa oculta pasa la información a la última capa, que produce la salida. La ventaja de la red neuronal es que es de naturaleza adaptativa. Aprende de la información proporcionada, es decir, se entrena a sí mismo a partir de los datos, que tienen un resultado conocido y optimiza sus pesos para una mejor predicción en situaciones con resultado desconocido.
Un perceptrón, a saber. red neuronal de una sola capa, es la forma más básica de una red neuronal. Un perceptrón recibe información multidimensional y la procesa mediante una suma ponderada y una función de activación. Se entrena mediante un algoritmo de aprendizaje y datos etiquetados que optimizan los pesos en el procesador de suma. Una limitación importante del modelo de perceptrón es su incapacidad para lidiar con la no linealidad. Una red neuronal multicapa supera esta limitación y ayuda a resolver problemas no lineales. La capa de entradaLa "capa de entrada" se refiere al nivel inicial en un proceso de análisis de datos o en arquitecturas de redes neuronales. Su función principal es recibir y procesar la información bruta antes de que esta sea transformada por capas posteriores. En el contexto de machine learning, una adecuada configuración de la capa de entrada es crucial para garantizar la efectividad del modelo y optimizar su rendimiento en tareas específicas.... se conecta con la capa oculta, que a su vez se conecta a la capa de salidaLa "capa de salida" es un concepto utilizado en el ámbito de la tecnología de la información y el diseño de sistemas. Se refiere a la última capa de un modelo de software o arquitectura que se encarga de presentar los resultados al usuario final. Esta capa es crucial para la experiencia del usuario, ya que permite la interacción directa con el sistema y la visualización de datos procesados..... Las conexiones se ponderan y las ponderaciones se optimizan mediante una regla de aprendizaje.
Hay muchas reglas de aprendizaje que se utilizan con la red neuronal:
a) mínimo cuadrado medio;
b) descenso de gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en...;
c) regla de Newton;
d) gradiente conjugado, etc.
Las reglas de aprendizaje se pueden utilizar junto con el método de error de propagación inversa. La regla de aprendizaje se utiliza para calcular el error en la unidad de salida. Este error se propaga hacia atrás a todas las unidades de manera que el error en cada unidad es proporcional a la contribución de esa unidad al error total en la unidad de salida. Los errores en cada unidad se utilizan para optimizar el peso en cada conexión. La Figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... 1 muestra la estructura de un modelo de red neuronal simple para una mejor comprensión.
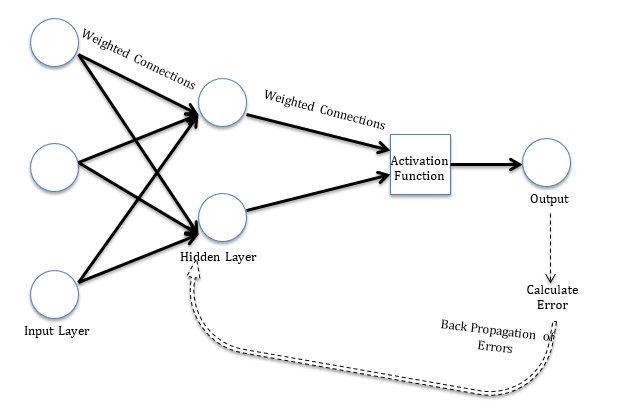
Figura 1 Un modelo de red neuronal simple
Ajuste de la red neuronal en R
Ahora ajustaremos un modelo de red neuronal en R. En este artículo, usamos un subconjunto del conjunto de datos de cereales compartido por la Universidad Carnegie Mellon (CMU). Los detalles del conjunto de datos se encuentran en el siguiente enlace: http://lib.stat.cmu.edu/DASL/Datafiles/Cereals.html. El objetivo es predecir la clasificación de las variables de los cereales como calorías, proteínas, grasas, etc. El guión R se proporciona uno al lado del otro y se comenta para una mejor comprensión del usuario. . Los datos están en formato .csv y se pueden descargar haciendo clic en: cereales.
Configure el directorio de trabajo en R usando setwd () función y mantenga cereal.csv en el directorio de trabajo. Usamos la calificación como variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente y las calorías, proteínas, grasas, sodio y fibra como variables independientes. Dividimos los datos en entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... y conjunto de prueba. El conjunto de entrenamiento se utiliza para encontrar la relación entre las variables dependientes e independientes, mientras que el conjunto de prueba evalúa el rendimiento del modelo. Usamos el 60% del conjunto de datos como conjunto de entrenamiento. La asignación de los datos al conjunto de entrenamiento y prueba se realiza mediante muestreo aleatorio. Realizamos un muestreo aleatorio en R usando muestra ( ) función. Hemos usado set.seed () para generar la misma muestra aleatoria cada vez y mantener la coherencia. Usaremos el índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... variable mientras se ajusta la red neuronal para crear conjuntos de datos de prueba y entrenamiento. El script R es el siguiente:
## Creating index variable
# Read the Data
data = read.csv("cereals.csv", header=T)
# Random sampling
samplesize = 0.60 * nrow(data)
set.seed(80)
index = sample( seq_len ( nrow ( data ) ), size = samplesize )
# Create training and test set
datatrain = data[ index, ]
datatest = data[ -index, ]
Ahora ajustamos una red neuronal a nuestros datos. Usamos neuralnet biblioteca para el análisis. El primer paso es escalar el conjunto de datos de cereales. La escala de los datos es esencial porque, de lo contrario, una variable puede tener un gran impacto en la variable de predicción solo debido a su escala. El uso sin escala puede dar lugar a resultados sin sentido. Las técnicas comunes para escalar datos son: normalizaciónLa normalización es un proceso fundamental en diversas disciplinas, que busca establecer estándares y criterios uniformes para mejorar la calidad y la eficiencia. En contextos como la ingeniería, la educación y la administración, la normalización facilita la comparación, la interoperabilidad y la comprensión mutua. Al implementar normas, se promueve la cohesión y se optimizan recursos, lo que contribuye al desarrollo sostenible y a la mejora continua de los procesos.... mínima-máxima, normalización de puntuación Z, medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... y MAD y estimadores de tan-h. La normalización mínimo-máximo transforma los datos en un rango común, eliminando así el efecto de escala de todas las variables. A diferencia de la normalización de la puntuación Z y el método de la mediana y la MAD, el método mínimo-máximo conserva la distribución original de las variables. Usamos la normalización mínimo-máximo para escalar los datos. El script R para escalar los datos es el siguiente.
## Scale data for neural network max = apply(data , 2 , max) min = apply(data, 2 , min) scaled = as.data.frame(scale(data, center = min, scale = max - min))
Los datos escalados se utilizan para adaptarse a la red neuronal. Visualizamos la red neuronal con pesos para cada una de las variables. El script R es el siguiente.
## Fit neural network
# install library
install.packages("neuralnet ")
# load library
library(neuralnet)
# creating training and test set
trainNN = scaled[index , ]
testNN = scaled[-index , ]
# fit neural network
set.seed(2)
NN = neuralnet(rating ~ calories + protein + fat + sodium + fiber, trainNN, hidden = 3 , linear.output = T )
# plot neural network
plot(NN)
La Figura 3 visualiza la red neuronal calculada. Nuestro modelo tiene 3 neuronas en su capa oculta. Las líneas negras muestran las conexiones con pesos. Los pesos se calculan utilizando el algoritmo de retropropagación explicado anteriormente. La línea azul muestra el término de sesgo.
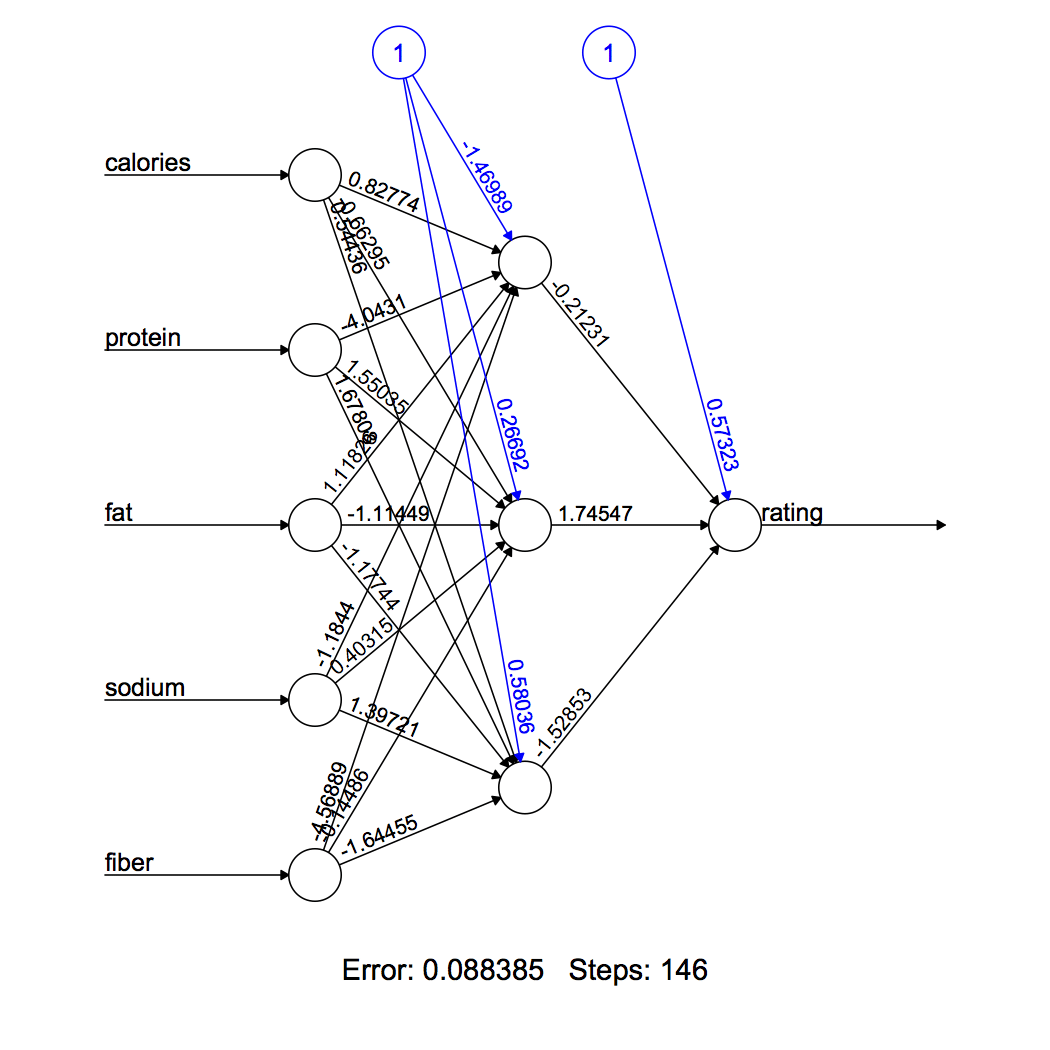
Figura 2 Red neuronal
Predecimos la calificación utilizando el modelo de red neuronal. El lector debe recordar que la calificación pronosticada será escalada y debe transformarla para poder hacer una comparación con la calificación real. También comparamos la calificación prevista con la calificación real mediante la visualización. El RMSE para el modelo de red neuronal es 6.05. El lector puede obtener más información sobre RMSE en otro artículo, al que se puede acceder haciendo clic en aquí. El script R es el siguiente:
## Prediction using neural network predict_testNN = compute(NN, testNN[,c(1:5)]) predict_testNN = (predict_testNN$net.result * (max(data$rating) - min(data$rating))) + min(data$rating) plot(datatest$rating, predict_testNN, col="blue", pch=16, ylab = "predicted rating NN", xlab = "real rating") abline(0,1) # Calculate Root Mean Square Error (RMSE) RMSE.NN = (sum((datatest$rating - predict_testNN)^2) / nrow(datatest)) ^ 0.5
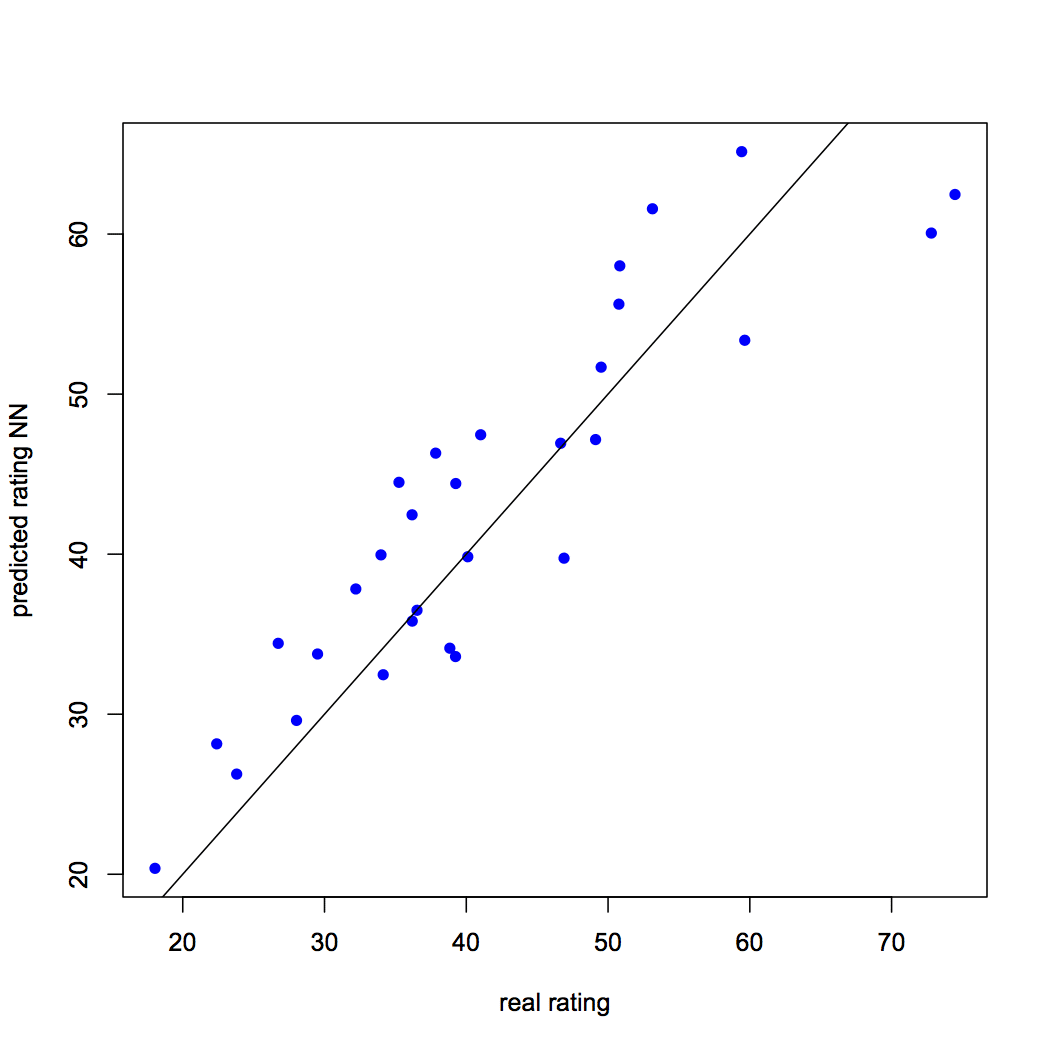
Figura 3: Calificación prevista frente a calificación real utilizando una red neuronal
Validación cruzada de una red neuronal
Hemos evaluado nuestro método de red neuronal utilizando RMSE, que es un método residual de evaluación. El principal problema de los métodos de evaluación residual es que no nos informa sobre el comportamiento de nuestro modelo cuando se introducen nuevos datos. Intentamos resolver el problema de los «datos nuevos» dividiendo nuestros datos en conjunto de entrenamiento y prueba, construyendo el modelo en conjunto de entrenamiento y evaluando el modelo calculando RMSE para el conjunto de prueba. La división de la prueba de entrenamiento no era más que la forma más simple de método de validación cruzada conocida como método de retención. Una limitación de la método de retención es la varianza de la métrica de evaluación del desempeño, en nuestro caso RMSE, puede ser alta en función de los elementos asignados al conjunto de entrenamiento y prueba.
La segunda técnica de validación cruzada comúnmente es validación cruzada de k-fold. Este método puede verse como recurrente método de retención. Los datos completos se dividen en k subconjuntos iguales y cada vez que se asigna un subconjunto como conjunto de prueba, se utilizan otros para entrenar el modelo. Cada punto de datos tiene la oportunidad de estar en el conjunto de prueba y en el conjunto de entrenamiento, por lo que este método reduce la dependencia del rendimiento en la división prueba-entrenamiento y reduce la varianza de las métricas de rendimiento. El caso extremo de validación cruzada de k-fold ocurrirá cuando k sea igual al número de puntos de datos. Significaría que el modelo predictivo se entrena sobre todos los puntos de datos excepto un punto de datos, que asume el papel de un conjunto de prueba. Este método de dejar un punto de datos como conjunto de prueba se conoce como dejar una validación cruzada.
Ahora realizaremos validación cruzada de k-fold en el modelo de red neuronal que construimos en la sección anterior. El número de elementos en el conjunto de entrenamiento, j, varían de 10 a 65 y para cada j, Se extraen 100 muestras del conjunto de datos. El resto de elementos en cada caso se asignan al conjunto de prueba. El modelo se entrena en cada uno de los 5600 conjuntos de datos de entrenamiento y luego se prueba en los conjuntos de prueba correspondientes. Calculamos el RMSE de cada uno de los conjuntos de prueba. Los valores de RMSE para cada uno de los conjuntos se almacenan en una matriz.[100 X 56]. Este método asegura que nuestros resultados estén libres de cualquier sesgo de la muestra y verifica la solidez de nuestro modelo. Empleamos bucle for anidado. El script R es el siguiente:
## Cross validation of neural network model
# install relevant libraries
install.packages("boot")
install.packages("plyr")
# Load libraries
library(boot)
library(plyr)
# Initialize variables
set.seed(50)
k = 100
RMSE.NN = NULL
List = list( )
# Fit neural network model within nested for loop
for(j in 10:65){
for (i in 1:k) {
index = sample(1:nrow(data),j )
trainNN = scaled[index,]
testNN = scaled[-index,]
datatest = data[-index,]
NN = neuralnet(rating ~ calories + protein + fat + sodium + fiber, trainNN, hidden = 3, linear.output= T)
predict_testNN = compute(NN,testNN[,c(1:5)])
predict_testNN = (predict_testNN$net.result*(max(data$rating)-min(data$rating)))+min(data$rating)
RMSE.NN [i]<- (sum((datatest$rating - predict_testNN)^2)/nrow(datatest))^0.5
}
List[[j]] = RMSE.NN
}
Matrix.RMSE = do.call(cbind, List)
Se puede acceder a los valores de RMSE mediante la variable Matrix.RMSE. El tamaño de la matriz es grande; por lo tanto, intentaremos darle sentido a los datos a través de visualizaciones. Primero, prepararemos un diagrama de caja para una de las columnas en Matrix.RMSE, donde el conjunto de entrenamiento tiene una longitud igual a 65. Se pueden preparar estos diagramas de cajaLos diagramas de caja, también conocidos como diagramas de caja y bigotes, son herramientas estadísticas que representan la distribución de un conjunto de datos. Estos diagramas muestran la mediana, los cuartiles y los valores atípicos, lo que permite visualizar la variabilidad y la simetría de los datos. Son útiles en la comparación entre diferentes grupos y en el análisis exploratorio, facilitando la identificación de tendencias y patrones en los datos.... para cada una de las longitudes del conjunto de entrenamiento (10 a 65). El script R es el siguiente.
## Prepare boxplot boxplot(Matrix.RMSE[,56], ylab = "RMSE", main = "RMSE BoxPlot (length of traning set = 65)")
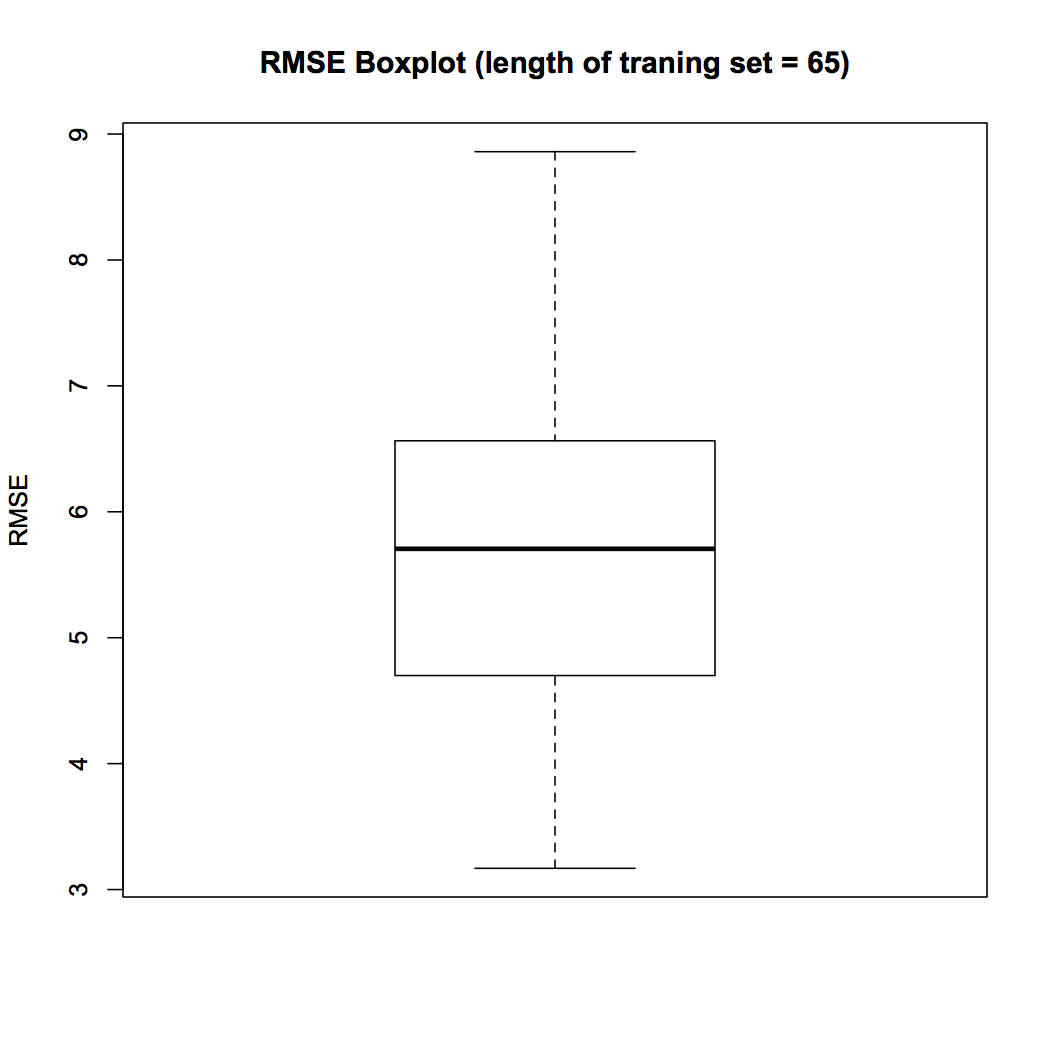
Figura 4 Diagrama de caja
El diagrama de caja de la Fig. 4 muestra que la mediana de RMSE en 100 muestras cuando la duración del conjunto de entrenamiento se fija en 65 es 5.70. En la siguiente visualización, estudiamos la variación de RMSE con la duración del conjunto de entrenamiento. Calculamos la mediana de RMSE para cada una de las longitudes del conjunto de entrenamiento y las trazamos usando el siguiente script R.
## Variation of median RMSE
install.packages("matrixStats")
library(matrixStats)
med = colMedians(Matrix.RMSE)
X = seq(10,65)
plot (med~X, type = "l", xlab = "length of training set", ylab = "median RMSE", main = "Variation of RMSE with length of training set")
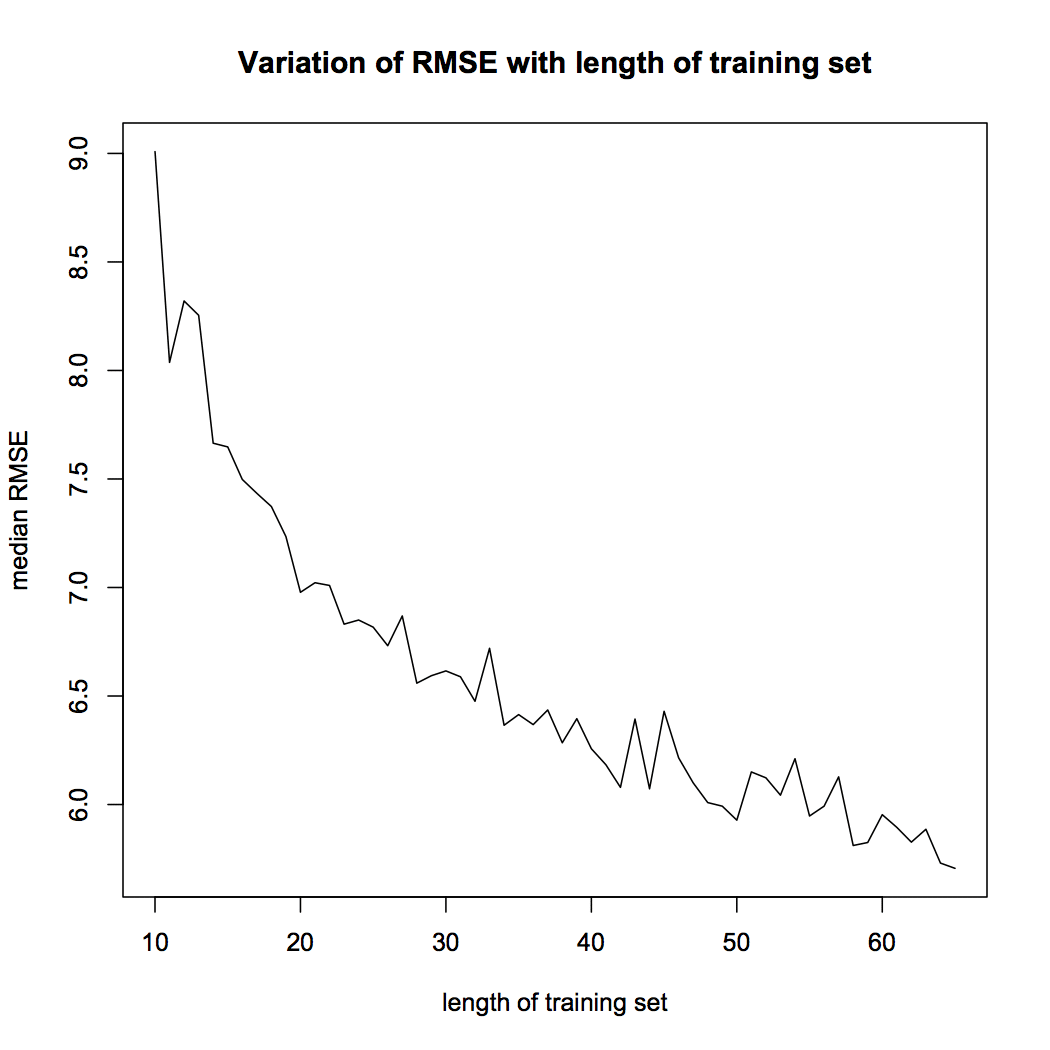
Figura 5 Variación de RMSE
La Figura 5 muestra que la mediana de RMSE de nuestro modelo disminuye a medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que la duración del entrenamiento de la serie. Este es un resultado importante. El lector debe recordar que la precisión del modelo depende de la duración del conjunto de entrenamiento. El rendimiento del modelo de red neuronal es sensible a la división de prueba de entrenamiento.
Notas finales
El artículo analiza los aspectos teóricos de una red neuronal, su implementación en R y la evaluación posterior al entrenamiento. La red neuronal está inspirada en el sistema nervioso biológico. Similar al sistema nervioso, la información pasa a través de capas de procesadores. La importancia de las variables está representada por los pesos de cada conexión. El artículo proporciona una comprensión básica del algoritmo de retropropagación, que se utiliza para asignar estos pesos. En este artículo también implementamos una red neuronal en R. Usamos un conjunto de datos disponible públicamente compartido por CMU. El objetivo es predecir la clasificación de los cereales utilizando información como calorías, grasas, proteínas, etc. Después de construir la red neuronal, evaluamos la precisión y robustez del modelo. Calculamos RMSE y realizamos análisis de validación cruzada. En la validación cruzada, verificamos la variación en la precisión del modelo a medida que cambia la duración del conjunto de entrenamiento. Consideramos conjuntos de entrenamiento con una longitud de 10 a 65. Para cada longitud, se seleccionan al azar 100 muestras y se calcula la mediana de RMSE. Mostramos que la precisión del modelo aumenta cuando el conjunto de entrenamiento es grande. Antes de utilizar el modelo para la predicción, es importante comprobar la solidez del rendimiento mediante la validación cruzada.
El artículo proporciona una revisión rápida de la red neuronal y es una referencia útil para los entusiastas de los datos. Hemos proporcionado un código R comentado a lo largo del artículo para ayudar a los lectores con la experiencia práctica en el uso de redes neuronales.
Bio: Chaitanya Sagar es el Fundador y CEO de Analítica perceptiva. Perceptive Analytics es una de las principales empresas de análisis de la India. Trabaja en Marketing Analytics para empresas de comercio electrónico, minoristas y farmacéuticas.






