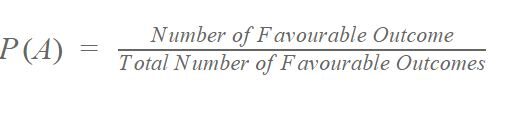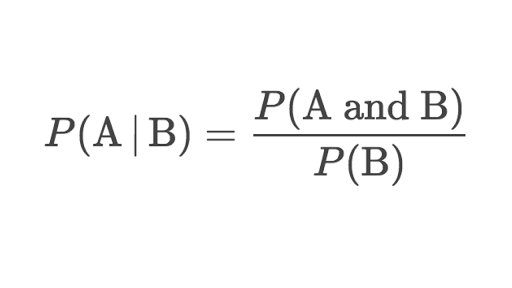La estadística es la gramática de la ciencia.
– Karl Pearson
¿Qué son los datos?
Los datos son la información recopilada a través de diferentes fuentes que pueden ser de naturaleza cualitativa o cuantitativa. En su mayoría, los datos recopilados se utilizan para analizar y obtener información sobre un tema en particular.
Por ejemplo:
1. Tamaño del cilindro, kilometraje, color, etc. para la venta de un automóvil
2.Si las células del cuerpo son malignas o benignas para detectar el cáncer
Tipos de datos
Datos numéricos
Los datos numéricos son la información en números, es decir, numérica que se presenta como una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... cuantitativa de las cosas.
Por ejemplo:
- Alturas y pesos de las personas
- Precios de las acciones
a) Datos discretos
Los datos discretos son la información que a menudo cuenta de algún evento, es decir, solo puede tomar valores específicos. A menudo se basan en números enteros, pero no necesariamente.
Por ejemplo:
- Número de veces que se lanzó una moneda
- Tallas de calzado de personas
b) Datos continuos
Los datos continuos son la información que tiene la posibilidad de tener valores infinitos, es decir, puede tomar cualquier valor dentro de un rango.
Por ejemplo:
¿Cuántos centímetros de lluvia cayeron en un día determinado?
Datos categóricos
Este tipo de datos es de naturaleza cualitativa y no tiene un significado matemático inherente. Es una especie de valor fijo bajo el cual se asigna o «categoriza» una unidad de observación.
Por ejemplo:
- Género
- Datos binarios (sí / no)
- Atributos de un vehículo como color, kilometraje, número de puertas, etc.
Datos ordinales
Este tipo de datos es la combinación de datos numéricos y categóricos, es decir, datos categóricos que tienen algún significado matemático.
Por ejemplo:
Calificaciones de restaurantes de 1 a 5, siendo 1 la más baja y 5 la más alta
ESTADÍSTICAS:
Media, mediana y moda
Significar
En matemáticas y estadística, la media es el promedio de las observaciones numéricas que es igual a la suma de las observaciones dividida por el número de observaciones.
dónde,
| = | significado aritmetico | |
| = | número de valores | |
| = | valores del conjunto de datos |
Mediana
La medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... de los datos, cuando se organizan en valor ascendente o descendente, es la observación central de los datos, es decir, el punto que separa la mitad superior de la mitad inferior de los datos.
Para calcular la mediana:
- Organice los datos en orden ascendente o descendente.
- un número impar de puntos de datos: el valor medio es la mediana.
- número par de puntos de datos: el promedio de los dos valores medios es la mediana.
| = | una lista ordenada de valores en el conjunto de datos | |
| = | número de valores en el conjunto de datos |
Modo
los modo de un conjunto de puntos de datos es el valor más frecuente.
Por ejemplo:
5, 2,6,5, 1,1,2,5, 3,8,5, 9,5 son el conjunto de puntos de datos. Aquí 5 es el modo porque ocurre con mayor frecuencia.
Varianza y desviación estándar
Diferencia
Matemáticamente y estadísticamente, diferencia se define como el promedio de las diferencias al cuadrado de la media. Pero para entender, esto describe cómo extendido los datos están en un conjunto de datos.
Los pasos para calcular la varianza usando un ejemplo:
Encontremos la varianza de (1,4,5,4,8)
- Encuentra la media de los puntos de datos es decir (1 + 4 + 5 + 4 + 8) / 5 = 4.4
- Encuentra las diferencias con la media es decir (-3,4, -0,4, 0,6, -0,4, 3,6)
- Encuentra las diferencias al cuadrado es decir (11,56, 0,16, 0,36, 0,16, 12,96)
- Encuentra el promedio de las diferencias al cuadrado es decir, 11,56 + 0,16 + 0,36 + 0,16 + 12,96 / 5 = 5,04
La fórmula para lo mismo es:
Desviación Estándar
La desviación estándar mide la variación o dispersión de los puntos de datos en un conjunto de datos. Representa la cercanía del punto de datos a la media y se calcula como la raíz cuadrada de la varianza.
En ciencia de datos, la desviación estándar se usa generalmente para identificar los valores atípicos en un conjunto de datos. Los puntos de datos que se encuentran a una desviación estándar de la media se consideran inusuales.
La fórmula para la desviación estándar es:
| = | desviación estándar de población | |
| = | el tamaño de la población | |
| = | cada valor de la población | |
| = | la media de la población |
Datos de población V / s Datos de muestra
Datos de población se refiere al conjunto de datos completo, mientras que Data de muestra se refiere a una parte de los datos de población que se utiliza para el análisis. El muestreo se realiza para facilitar el análisis.
Cuando se utilizan datos de muestra para el análisis, la fórmula de varianza es ligeramente diferente. Si hay un total de n muestras, dividimos por n-1 en lugar de n:
| = | varianza de la muestra | |
| = | el valor de una observación | |
| = | el valor medio de las observaciones | |
| = | el número de observaciones |
PROBABILIDAD:
¿Qué es la probabilidad?
El concepto de probabilidad es extremadamente simple. Significa la probabilidad de que ocurra un evento o la probabilidad de que ocurra un evento.
La fórmula de probabilidad es:
Por ejemplo:
La probabilidad de que la moneda muestre cara cuando se lanza es de 0,5.
La probabilidad condicional
La probabilidad condicional es la probabilidad de que ocurra un evento siempre que ya haya ocurrido otro evento.
La fórmula de la probabilidad condicional:
Por ejemplo:
Los alumnos de una clase han realizado dos pruebas de la asignatura Matemáticas. En la primera prueba, el 60% de los alumnos aprueba mientras que solo el 40% de los alumnos aprueban ambas pruebas. ¿Qué porcentaje de estudiantes que aprobaron la primera prueba, aprobaron la segunda prueba?

Teorema de Bayes
El teorema de Bayes es un concepto estadístico muy importante que se utiliza en muchas industrias, como la salud y las finanzas. La fórmula de probabilidad condicional que hemos hecho anteriormente también se ha derivado de este teorema.
Se utiliza para calcular la probabilidad de una hipótesis en función de las probabilidades de varios datos proporcionados en la hipótesis.
La fórmula del teorema de Bayes es:
| = | eventos | |
| = | probabilidad de A dado B es verdadera | |
| = | probabilidad de B dada A es verdadera | |
| = | las probabilidades independientes de A y B |
Por ejemplo:
Supongamos que existe una prueba del VIH que puede identificar a los pacientes VIH + positivos con precisión el 99% de las veces, y que también tiene un resultado negativo con precisión para el 99% de las personas VIH negativas. Aquí, solo el 0,3% de la población total es seropositiva.

CONCLUSIÓN
Los temas de estadística y probabilidad cubiertos en el artículo son realmente importantes, pero hay muchos otros temas como las funciones de distribución de probabilidad y sus tipos, covarianza y correlación, etc.que no se han cubierto aquí porque requieren atención separada debido a su gráfico. naturaleza.
Las matemáticas y las estadísticas son el corazón de la ciencia de datos. Los temas cubiertos en este artículo son la base de muchos algoritmos, fórmulas de cálculo de errores y comprensión gráfica de las cosas, por lo que son muy importantes y no pueden ignorarse.