Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Hoy, hablemos de uno de los conceptos fundamentales de la estadística: las distribuciones de probabilidad. Ayudan a comprender mejor los datos y actúan como base para comprender más conceptos estadísticos, como los intervalos de confianza y las pruebas de hipótesis.
Definición informal
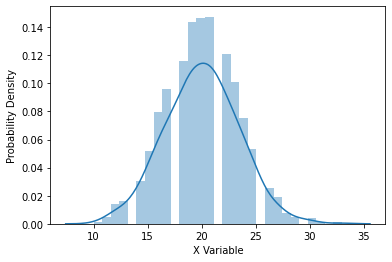
Sea X una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria que tiene más de un resultado posible. Grafique la probabilidad en el eje y y el resultado en el eje x. Si repetimos el experimento muchas veces y graficamos la probabilidad de cada resultado posible, obtenemos una gráfica que representa las probabilidades. Esta gráfica se llama distribución de probabilidad (PD). La altura de la gráfica para X da la probabilidad de ese resultado.
Tipos de distribuciones de probabilidad
Hay dos tipos de distribuciones según el tipo de datos generados por los experimentos.
1. Distribuciones de probabilidad discretas
Estas distribuciones modelan las probabilidades de variables aleatorias que pueden tener valores discretos como resultados. Por ejemplo, los valores posibles para la variable aleatoria X que representa el número de caras que pueden ocurrir cuando se lanza una moneda dos veces son el conjunto {0, 1, 2} y no cualquier valor de 0 a 2 como 0.1 o 1.6.
Ejemplos: Bernoulli, Binomial, Binomial negativo, Hipergeométrico, etc.,
2. Distribuciones de probabilidad continua
Estas distribuciones modelan las probabilidades de variables aleatorias que pueden tener cualquier resultado posible. Por ejemplo, los valores posibles para la variable aleatoria X que representa el peso de los ciudadanos en una ciudad que puede tener cualquier valor como 34,5, 47,7, etc.
Ejemplos: Normal, T de Student, Chi-cuadrado, Exponencial, etc.,
Terminologias
Cada DP nos proporciona información adicional sobre el comportamiento de los datos involucrados. Cada PD viene dada por una función de probabilidad que generaliza las probabilidades de los resultados.
Con esto, podemos estimar la probabilidad de un resultado particular (discreto) o la probabilidad de que se encuentre dentro de un rango particular de valores para cualquier resultado dado (continuo). La función se denomina función de masa de probabilidad (PMF) para distribuciones discretas y función de densidad de probabilidad (PDF) para distribuciones continuas. El valor total de PMF y PDF en todo el dominio siempre es igual a uno.
Función de distribución acumulativa
La PDF proporciona la probabilidad de un resultado particular, mientras que la Función de distribución acumulativa proporciona la probabilidad de ver un resultado menor o igual que un valor particular de la variable aleatoria. Los CDF se utilizan para comprobar cómo se ha sumado la probabilidad hasta cierto punto. Por ejemplo, si P (X = 5) es la probabilidad de que el número de caras al lanzar una moneda sea 5, P (X <= 5) denota la probabilidad acumulada de obtener de 1 a 5 caras.
Las funciones de distribución acumulativa también se utilizan para calcular los valores p como parte de la realización de pruebas de hipótesis.
Distribuciones de probabilidad discretas
Hay muchas distribuciones de probabilidad discretas para usar en diferentes escenarios. Discutiremos las distribuciones discretas en esta publicación. Las distribuciones binomial y de Poisson son las más discutidas en la siguiente lista.
1. Distribución de Bernoulli
Esta distribución se genera cuando realizamos un experimento una vez y solo tiene dos resultados posibles: éxito y fracaso. Los ensayos de este tipo se denominan ensayos de Bernoulli, que forman la base de muchas distribuciones que se analizan a continuación. Sea p la probabilidad de éxito y 1 – p es la probabilidad de fracaso.
El PMF se da como
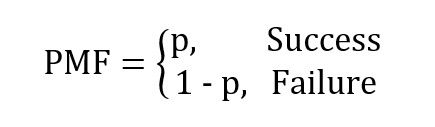
Un ejemplo de esto sería lanzar una moneda una vez. p es la probabilidad de salir adelante y 1 – p es la probabilidad de obtener cola. Tenga en cuenta que el éxito y el fracaso son subjetivos y los definimos según el contexto.
2. Distribución binomial
Esto se genera para variables aleatorias con solo dos resultados posibles. Sea p la probabilidad de que un evento sea un éxito, lo que implica que 1 – p es la probabilidad de que el evento sea un fracaso. Realizar el experimento repetidamente y graficar la probabilidad cada vez nos da la distribución Binomial.
El ejemplo más común dado para la distribución binomial es el de lanzar una moneda n número de veces y calcular las probabilidades de obtener un número particular de caras. Más ejemplos del mundo real incluyen la cantidad de llamadas de ventas exitosas para una empresa o si un medicamento funciona para una enfermedad o no.
El PMF se da como,
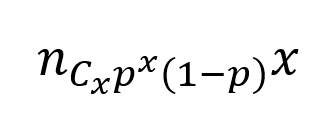
donde p es la probabilidad de éxito, n es el número de intentos y x es el número de veces que obtenemos un éxito.
3. Distribución hipergeométrica
Considere el caso de sacar una canica roja de una caja de canicas de diferentes colores. El evento de sacar una bola roja es un éxito y no sacarla es un fracaso. Pero cada vez que se saca una canica, no se devuelve a la caja y, por lo tanto, esto afecta la probabilidad de sacar una bola en la siguiente prueba. La distribución hipergeométrica modela la probabilidad de k éxitos en n ensayos donde cada ensayo se realiza sin reemplazo. Esto es diferente a la distribución binomial donde la probabilidad permanece constante durante los ensayos.
El PMF se da como,
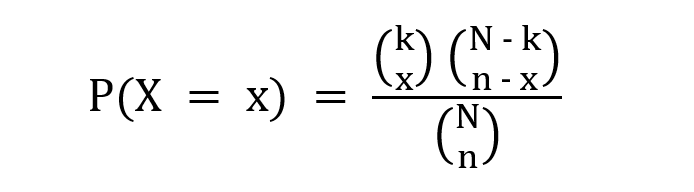
donde k es el número de posibles éxitos, x es el número deseado de éxitos, N es el tamaño de la población yn es el número de ensayos.
4. Distribución binomial negativa
A veces queremos comprobar cuántas pruebas de Bernoulli necesitamos hacer para obtener un resultado en particular. El resultado deseado se especifica de antemano y continuamos el experimento hasta que se logre. Consideremos el ejemplo de tirar un dado. Nuestro resultado deseado, definido como un éxito, es obtener un 4. Queremos saber la probabilidad de obtener este resultado tres veces. Esto se interpreta como el número de fallas (otros números aparte de 4) que ocurrirán antes de que veamos el tercer éxito.
El PMF se da como,
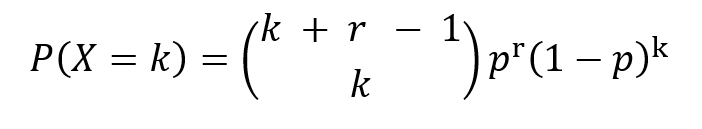
donde p es la probabilidad de éxito, k es el número de fracasos observados y r es el número deseado de éxitos hasta que se detenga el experimento.
Al igual que en la distribución binomial, la probabilidad a través de los ensayos permanece constante y cada ensayo es independiente del otro.
5. Distribución geométrica
Este es un caso especial de distribución binomial negativa donde el número deseado de éxitos es 1. Mide el número de fracasos que obtenemos antes de un éxito. Usando el mismo ejemplo dado en la sección anterior, nos gustaría saber el número de fallas que vemos antes de obtener las primeras 4 al lanzar los dados.
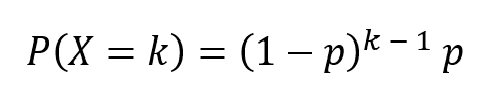
donde p es la probabilidad de éxito y k es el número de fracasos. Aquí, r = 1.
6. Distribución de veneno
Esta distribución describe los eventos que ocurren en un intervalo fijo de tiempo o espacio. Un ejemplo podría aclarar esto. Considere el caso del número de llamadas que recibe un centro de atención al cliente por hora. Podemos estimar el número promedio de llamadas por hora, pero no podemos determinar el número exacto y la hora exacta a la que hay una llamada. Cada ocurrencia de un evento es independiente de las otras ocurrencias.
El PMF se da como,
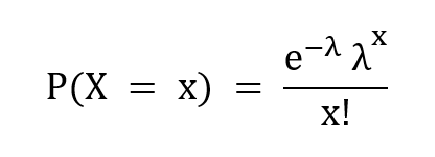
donde λ es el número promedio de veces que ha ocurrido el evento en un cierto período de tiempo, x es el resultado deseado ye es el número de Euler.
7. Distribución multinomial
En las distribuciones anteriores, solo hay dos resultados posibles: éxito y fracaso. Sin embargo, la distribución multinomial describe las variables aleatorias con muchos resultados posibles. En ocasiones, esto también se denomina distribución categórica, ya que cada resultado posible se trata como una categoría separada. Considere el escenario de jugar un juego n veces. La distribución multinomial nos ayuda a determinar la probabilidad combinada de que el jugador 1 gane x1 veces, el jugador 2 ganará x2 veces y el jugador k gana Xk veces.
El PMF se da como,
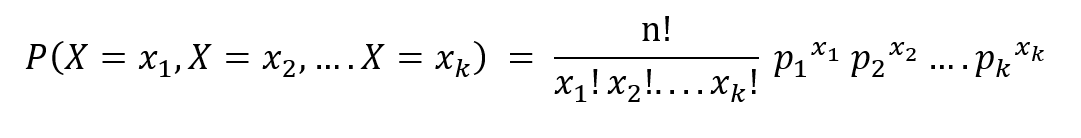
donde n es el número de ensayos, p1,……pagk denotar las probabilidades de los resultados x1……Xk respectivamente.
En esta publicación, hemos definido distribuciones de probabilidad y discutimos brevemente diferentes distribuciones de probabilidad discretas. Déjame saber tu opinión sobre el artículo en la sección de comentarios a continuación.
Referencias
1. https://www.statisticshowto.com/
2. https://stattrek.com/
3. Wikipedia
Sobre mí
Soy un ex ingeniero de software que trabaja en la transición a la ciencia de datos. Soy estudiante de maestría en Data Science. No dude en conectarse conmigo en https://www.linkedin.com/in/priyanka-madiraju/
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






