Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Análisis de supervivencia
El análisis de supervivencia es una rama importante de la estadística que se tiene en cuenta para responder a todas estas preguntas.
El estudio de Análisis de supervivencia debe definir un marco de tiempo en el que se lleva a cabo este estudio. Como en muchos casos, es posible que el período de tiempo dado para que ocurra el evento sea el mismo entre sí. El análisis de supervivencia implica el modelado de datos de tiempo hasta el evento. Por lo tanto, necesitamos definir el contexto del análisis de supervivencia en el estudio como el tiempo como el «evento» en el contexto del análisis de supervivencia.
Hay diferentes formas en las que realizamos el análisis de supervivencia. Se realiza de varias formas, como cuando definimos un grupo. Algunos de ellos son curvas de Kaplan Meier, modelos de regresión de Cox, función de peligro, función de supervivencia, etc.
Cuando se realiza el análisis de supervivencia para comparar el análisis de supervivencia de dos grupos diferentes. Allí realizamos la prueba Log-Rank.
Cuando al análisis de supervivencia le gusta describir las variables categóricas y cuantitativas sobre la supervivencia, nos gusta hacer la regresión de riesgos proporcionales de Cox, modelos paramétricos de supervivencia, etc.
En el análisis de supervivencia, necesitamos definir ciertos términos antes de proceder, como el evento, el tiempo, la censura, la función de supervivencia, etc.
Evento, cuando hablamos de, es la actividad que está sucediendo o va a ocurrir en el estudio de análisis de supervivencia, como la muerte de una persona por una enfermedad en particular, el tiempo para obtener la curación mediante un diagnóstico médico, el tiempo para curarse con las vacunas, el momento de la aparición de la falla de máquinas en el piso de fabricación, tiempo para la aparición de enfermedades, etc.
Tiempo
en el estudio de caso de análisis de supervivencia es el tiempo desde el comienzo de la observación del análisis de supervivencia sobre el tema hasta el momento en que ocurrirá el evento. Como en el caso de una máquina mecánica a una falla, necesitamos conocer el
(a) hora de un evento cuando la máquina se pondrá en marcha
(b) cuándo fallará la máquina
(c) pérdida de la máquina o apagado de la máquina del estudio de análisis de supervivencia.
Censura / Observación censurada
Esta terminología se define como si el tema sobre el que estamos haciendo el estudio de análisis de supervivencia no se ve afectado por el evento de estudio definido, entonces se describen como censurados. Es posible que el sujeto censurado tampoco tenga un evento después del final de la observación del análisis de supervivencia. El sujeto se llama censurado en el sentido de que no se observó nada fuera del sujeto después del tiempo de censura.
Censura de la observación también son de 3 tipos-
1. Derecho censurado
La censura por la derecha se utiliza en muchos problemas. Ocurre cuando no estamos seguros de lo que les sucedió a las personas después de un cierto punto en el tiempo.
Ocurre cuando el tiempo real del evento es mayor que el tiempo censurado cuando c <t. Esto sucede si algunas personas no pueden ser seguidas durante todo el tiempo porque murieron o se perdieron durante el seguimiento o se retiraron del estudio.
2. Censurado a la izquierda
La censura de izquierda es cuando no estamos seguros de lo que le sucedió a la gente antes de algún momento. La censura por la izquierda es lo opuesto, que ocurre cuando el tiempo real del evento es menor que el tiempo censurado cuando c> t.
3. Intervalo censurado
La censura de intervalo es cuando sabemos que algo ha sucedido en un intervalo (no antes de la hora de inicio ni después de la hora de finalización del estudio) pero no sabemos exactamente cuándo sucedió en el intervalo.
La censura de intervalo es una concatenación de la censura de izquierda y derecha cuando se sabe que el tiempo ha ocurrido entre dos puntos de tiempo.
Función de supervivencia S
Aquí, discutiremos el EstimadorEl "Estimador" es una herramienta estadística utilizada para inferir características de una población a partir de una muestra. Se basa en métodos matemáticos para proporcionar estimaciones precisas y confiables. Existen diferentes tipos de estimadores, como los insesgados y los consistentes, que se eligen según el contexto y el objetivo del estudio. Su correcto uso es fundamental en investigaciones científicas, encuestas y análisis de datos.... de Kaplan Meier.
Estimador de Kaplan Meier
El estimador de Kaplan Meier se utiliza para estimar la función de supervivencia para los datos de por vida. Es una técnica de estadística no paramétrica. También se conoce como estimador de límite de producto, y el concepto radica en estimar el tiempo de supervivencia durante un cierto tiempo de un evento médico importante, un momento determinado de muerte, falla de la máquina o cualquier evento significativo importante.
Hay muchos ejemplos como
1. Fallo de las piezas de la máquina después de varias horas de funcionamiento.
2. Cuánto tiempo tardará la vacuna COVID 19 en curar al paciente.
3. Cuánto tiempo se requiere para obtener una cura a partir de un diagnóstico médico, etc.
4. Estimar cuántos empleados dejarán la empresa en un período de tiempo específico.
5. ¿Cuántos pacientes se curarán con el cáncer de pulmón?
Para estimar la supervivencia de Kaplan Meier, primero necesitamos estimar la función de supervivencia S
Donde (d) es el número de eventos de muerte en el momento
Supuestos de supervivencia de Kaplan Meier
En los casos de la vida real, no tenemos una idea de la verdadera función de la tasa de supervivencia. Por lo tanto, en el Estimador de Kaplan Meier estimamos y aproximamos la función de supervivencia real a partir de los datos del estudio. Hay 3 supuestos de Kaplan Meier Survival
1) Las probabilidades de supervivencia son las mismas para todas las muestras que se unieron al final del estudio y las que se incorporaron antes. No se supone que cambie el análisis de supervivencia que puede afectar.
2) La ocurrencia de un evento se realiza en un momento específico.
3) La censura del estudio no depende del resultado. El método de Kaplan Meier no depende del resultado de interés.
La interpretación del análisis de supervivencia es el eje Y muestra la probabilidad de un sujeto que no se ha incluido en el estudio de caso. El eje X muestra la representación del interés del sujeto después de sobrevivir hasta el tiempo. Cada caída en la función de supervivencia (aproximada por el estimador de Kaplan-Meier) es causada por el evento de interés que ocurre durante al menos una observación.
La gráfica suele ir acompañada de intervalos de confianza, para describir la incertidumbre acerca de las estimaciones puntuales (los intervalos de confianza más amplios muestran una alta incertidumbre, esto sucede cuando tenemos unos pocos participantes) ocurre tanto en las observaciones que mueren como en las que están siendo censuradas.
Aspectos importantes a tener en cuenta para el análisis del estimador de Kaplan Meier
1) Necesitamos realizar la prueba de rango logarítmico para hacer cualquier tipo de inferencia.
2) Los resultados de Kaplan Meier pueden estar fácilmente sesgados. El Kaplan Meier es un enfoque univariado para resolver el problema.
3) La eliminación de datos censurados provocará un cambio en la forma de la curva. Esto creará sesgos en el ajuste del modelo.
4) Las pruebas y observaciones estadísticas se vuelven engañosas si se realiza la dicotomía de variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... continua.
5) Al dicotomizar los medios, tomamos medidas estadísticas como la medianaLa mediana es una medida estadística que representa el valor central de un conjunto de datos ordenados. Para calcularla, se organizan los datos de menor a mayor y se identifica el número que se encuentra en el medio. Si hay un número par de observaciones, se promedia los dos valores centrales. Este indicador es especialmente útil en distribuciones asimétricas, ya que no se ve afectado por valores extremos.... para crear grupos, pero esto puede generar problemas en el conjunto de datos.
Tomemos el ejemplo en Python
Enlace a Notebook- (https://drive.google.com/file/d/1VGKZNViDbx4rx_7lGMCA6dgU3XuMKGVU/view?usp=sharing)
Importemos la biblioteca importante necesaria para trabajar en Python
Primero, estamos importando diferentes bibliotecas de Python para nuestro trabajo. Aquí, tomamos el conjunto de datos de cáncer de pulmón. Después de las bibliotecas y la carga, leeremos los datos usando la biblioteca de pandas. El conjunto de datos contiene información diferente
Tratamiento 1 = estándar, 2 = prueba, Tipo de célula 1 = escamosa, 2 = pequeña
celular, 3 = adeno, 4 = grande, Supervivencia en días, Estado 1 = muerto, 0 = censurado, Puntaje de Karnofsky (una medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... del desempeño general, 100 = mejor), Meses desde el diagnóstico, Edad en años Terapia previa 0 = no, 10 = sí, etc.
Aquí vemos la cabeza y la cola.
Ahora, aquí importamos el código Python para realizar el Estimador de Kaplan Meier
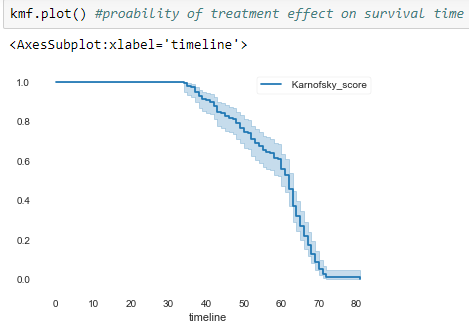
Aquí, realizamos el análisis en la puntuación de Karnofsky, el eje x representa la línea de tiempo y el eje y muestra la puntuación. La mejor puntuación es 1, significa que el sujeto es apto, una puntuación de 0 significa la peor puntuación.
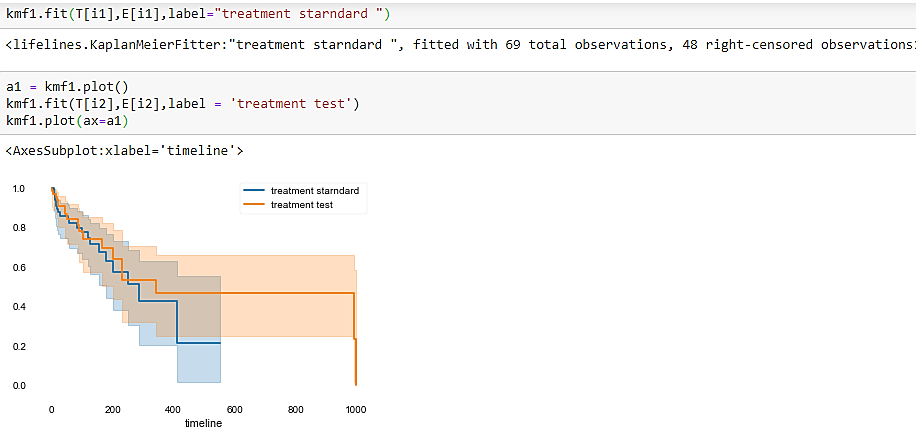
Luego aplicamos el código de Supervivencia, Terapia Previa, el tratamiento aquí haremos el Análisis Estimador de Kaplan Meier.
Entonces, encajamos kmf1 = KaplanMeierFitter () para ajustar la función de Kaplan Meier y ejecutamos el siguiente código para diferentes datos relacionados con los problemas del cáncer de pulmón.
El estimador de Kaplan Meier después de ejecutar el código muestra el gráfico entre el estándar de prueba de tratamiento y la prueba de tratamiento.
En este artículo, mi objetivo clave fue explicar el análisis de supervivencia con el estimador de Kaplan Meier. Las cosas relacionadas con él y una descripción del problema en la vida real.
Ventajas y desventajas de Kaplan Meier Estimator
Ventajas
1) No requiere demasiadas funciones; solo se requiere tiempo para el evento de análisis de supervivencia.
2) Proporciona una descripción general promedio relacionada con el evento.
Desventajas
1) Muchas variables no pueden correlacionarse y monitorearse simultáneamente.
2) Si se eliminan los datos de censura, el modelo se sesgará en el momento del ajuste.
3) No se puede predecir la estimación adecuada de la magnitud del cambio en el evento.
