Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
La agrupación en clústeres es una técnica de aprendizaje automático no supervisada. Es el proceso de división del conjunto de datos en grupos en los que los miembros del mismo grupo poseen características similares. Los algoritmos de agrupación en clúster más utilizados son agrupación de K-medias, agrupación jerárquica, agrupación basada en densidad, agrupación basada en modelos, etc. En este artículo, vamos a discutir el agrupamientoEl "agrupamiento" es un concepto que se refiere a la organización de elementos o individuos en grupos con características o objetivos comunes. Este proceso se utiliza en diversas disciplinas, incluyendo la psicología, la educación y la biología, para facilitar el análisis y la comprensión de comportamientos o fenómenos. En el ámbito educativo, por ejemplo, el agrupamiento puede mejorar la interacción y el aprendizaje entre los estudiantes al fomentar el trabajo... de K-Means en detalle.
Agrupación de K-medias
Es el algoritmo de aprendizaje no supervisadoEl aprendizaje no supervisado es una técnica de machine learning que permite a los modelos identificar patrones y estructuras en datos sin etiquetas predefinidas. A través de algoritmos como k-means y análisis de componentes principales, este enfoque se utiliza en diversas aplicaciones, como la segmentación de clientes, la detección de anomalías y la compresión de datos. Su capacidad para revelar información oculta lo convierte en una herramienta valiosa en la... de tipo iterativo más simple y de uso común. En esto, inicializamos aleatoriamente el K número de centroides en los datos (el número de k se encuentra utilizando el Codo método que se discutirá más adelante en este artículo) e itera estos centroides hasta que no ocurra ningún cambio en la posición del centroide. Repasemos los pasos involucrados en K significa agrupamiento para una mejor comprensión.
1) Seleccione la cantidad de clústeres para el conjunto de datos (K)
2) Seleccione K número de centroides
3) Al calcular la distancia euclidiana o la distancia de Manhattan, asigne los puntos a la centroide más cercano, creando así K grupos
4) Ahora encuentre el centroide original en cada grupo
5) Reasigne nuevamente todo el punto de datos basado en este nuevo centroide, luego repita el paso 4 hasta que la posición del centroide no cambie.
Encontrar el número óptimo de clústeres es una parte importante de este algoritmo. Un método comúnmente utilizado para encontrar el valor óptimo de K es Método del codo.
Método del codo
En el método del codo, en realidad estamos variando el número de conglomerados (K) de 1 a 10. Para cada valor de K, estamos calculando WCSS (Suma del cuadrado dentro del conglomerado). WCSS es la suma de la distancia al cuadrado entre cada punto y el centroide en un grupo. Cuando graficamos el WCSS con el valor K, el gráfico parece un codo. A medida que aumenta el número de clústeres, el valor WCSS comenzará a disminuir. El valor WCSS es mayor cuando K = 1. Cuando analizamos el gráfico, podemos ver que el gráfico cambiará rápidamente en un punto y, por lo tanto, creará una forma de codo. A partir de este punto, el gráfico comienza a moverse casi en paralelo al eje X. El valor de K correspondiente a este punto es el valor de K óptimo o un número óptimo de conglomerados.
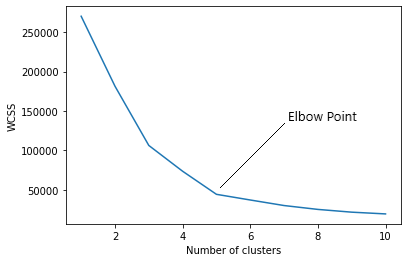
Ahora implementemos la agrupación en clústeres de K-Means usando Python.
Implementación
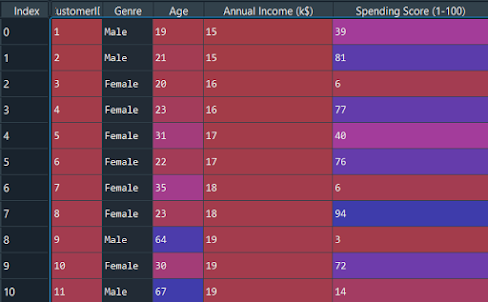
En primer lugar, tenemos que importar bibliotecas esenciales.
import numpy as np import matplotlib.pyplot as plt import pandas as pd import sklearn
Ahora importemos el conjunto de datos y separemos las características importantes.
dataset = pd.read_csv('Mall_Customers.csv') X = dataset.iloc[:, [3, 4]].values
Tenemos que encontrar el valor óptimo de K para agrupar los datos. Ahora estamos usando el método del codo para encontrar el valor óptimo de K.
from sklearn.cluster import KMeans wcss = [] for i in range(1, 11): kmeans = KMeans(n_clusters = i, init="k-means++", random_state = 42) kmeans.fit(X) wcss.append(kmeans.inertia_)
El argumento «init» es el método para inicializar el centroide. Calculamos el valor WCSS para cada valor K. Ahora tenemos que trazar el WCSS con valor K
plt.plot(range(1, 11), wcss) plt.xlabel('Number of clusters') plt.ylabel('WCSS') plt.show(
El gráfico será-
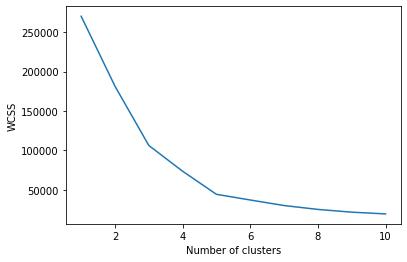
El punto en el que se crea la forma del codo es 5, es decir, nuestro valor K o un número óptimo de conglomerados es 5. Ahora entrenemos el modelo en el conjunto de datos con un número de conglomerados 5.
kmeans = KMeans(n_clusters = 5, init = "k-means++", random_state = 42) y_kmeans = kmeans.fit_predict(X)
y_kmeans será:
array([3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0,
3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 0, 3, 1,
3, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 4, 2, 1, 2, 4, 2, 4, 2,
1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 1, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2, 4, 2,
4, 2])plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c="red", label="Cluster1") plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c="blue", label="Cluster2") plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c="green", label="Cluster3) plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c = "violet', label="Cluster4") plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 60, c="yellow", label="Cluster5") plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c="black", label="Centroids") plt.xlabel('Annual Income (k$)') plt.ylabel('Spending Score (1-100)') plt.legend() plt.show()
Grafico:
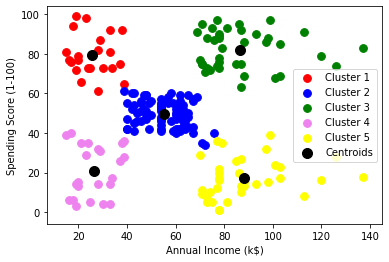
Como puede ver hay 5 grupos en total los cuales se visualizan en diferentes colores y el centroide de cada grupo se visualiza en color negro.
Código completo
# Importing the libraries import numpy as np import matplotlib.pyplot as plt import pandas as pd # Importing the dataset X = dataset.iloc[:, [3, 4]].values dataset = pd.read_csv('Mall_Customers.csv') from sklearn.cluster import KMeans # Using the elbow method to find the optimal number of clusters wcss = [] for i in range(1, 11): wcss.append(kmeans.inertia_) kmeans = KMeans(n_clusters = i, init="k-means++", random_state = 42) kmeans.fit(X) plt.plot(range(1, 11), wcss) plt.xlabel('Number of clusters') y_kmeans = kmeans.fit_predict(X) plt.ylabel('WCSS') plt.show() # Training the K-Means model on the dataset kmeans = KMeans(n_clusters = 5, init="k-means++", random_state = 42) y_kmeans = kmeans.fit_predict(X) # Visualising the clusters plt.scatter( X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 60, c="blue", label="Cluster2") plt.scatter( X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 60, c="red", label="Cluster1") plt.scatter( X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 60, c="green", label="Cluster3") plt.scatter( kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 100, c="black", label="Centroids") plt.scatter( X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 60, c="violet", label="Cluster4") plt.scatter( X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 60, c="yellow", label="Cluster5") plt.xlabel('Annual Income (k$)') plt.ylabel('Spending Score (1-100)') plt.legend() plt.show()
Conclusión
Se trata del concepto básico del algoritmo de agrupación en clústeres de K-medias en el aprendizaje automático. En los próximos artículos, podemos obtener más información sobre diferentes algoritmos de aprendizaje automático.
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.
