Nota: Este artículo se publicó originalmente el 10 de octubre de 2014 y se actualizó el 27 de marzo de 2018.
Visión general
- Comprender k vecino más cercano (KNN): uno de los algoritmos de aprendizaje automático más populares
- Aprenda el funcionamiento de kNN en python
- Elija el valor correcto de k en lenguaje sencillo
Introducción
En los cuatro años de mi carrera de ciencia de datos, He construido más del 80% de modelos de clasificación y solo un 15-20% de modelos de regresión. Estas proporciones pueden generalizarse más o menos en toda la industria. La razón detrás de este sesgo hacia modelos de clasificación es que la mayoría de los problemas analíticos implican tomar una decisión.
Por ejemplo, si un cliente se desgastará o no, si nos dirigimos al cliente X para campañas digitales, si el cliente tiene un alto potencial o no, etc. Estos análisis son más perspicaces y están directamente vinculados a una hoja de ruta de implementación.
En este artículo, hablaremos sobre otro aprendizaje automático ampliamente utilizado. técnica de clasificaciónmi llamados vecinos K-más cercanos (KNN). Nuestro enfoque estará principalmente en cómo funciona el algoritmo y cómo el parámetro de entrada afecta la salida / predicción.
Nota: Las personas que prefieren aprender a través de videos pueden aprender lo mismo a través de nuestro curso gratuito – Algoritmo K-Vecinos más cercanos (KNN) en Python y R. Y si es un principiante absoluto en la ciencia de datos y el aprendizaje automático, consulte nuestro programa Certified BlackBelt:
Tabla de contenido
- ¿Cuándo usamos el algoritmo KNN?
- ¿Cómo funciona el algoritmo KNN?
- ¿Cómo elegimos el factor K?
- Breaking it Down – Pseudo código de KNN
- Implementación en Python desde cero
- Comparando nuestro modelo con scikit-learn
¿Cuándo usamos el algoritmo KNN?
KNN se puede utilizar para problemas predictivos de clasificación y regresión. Sin embargo, se usa más ampliamente en problemas de clasificación en la industria. Para evaluar cualquier técnica, generalmente nos fijamos en 3 aspectos importantes:
1. Facilidad para interpretar la salida
2. Tiempo de cálculo
3. Poder predictivo
Tomemos algunos ejemplos para colocar KNN en la escala:
Ferias de algoritmos KNN a través de todos los parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... de consideraciones. Se utiliza comúnmente por su fácil interpretación y bajo tiempo de cálculo.
¿Cómo funciona el algoritmo KNN?
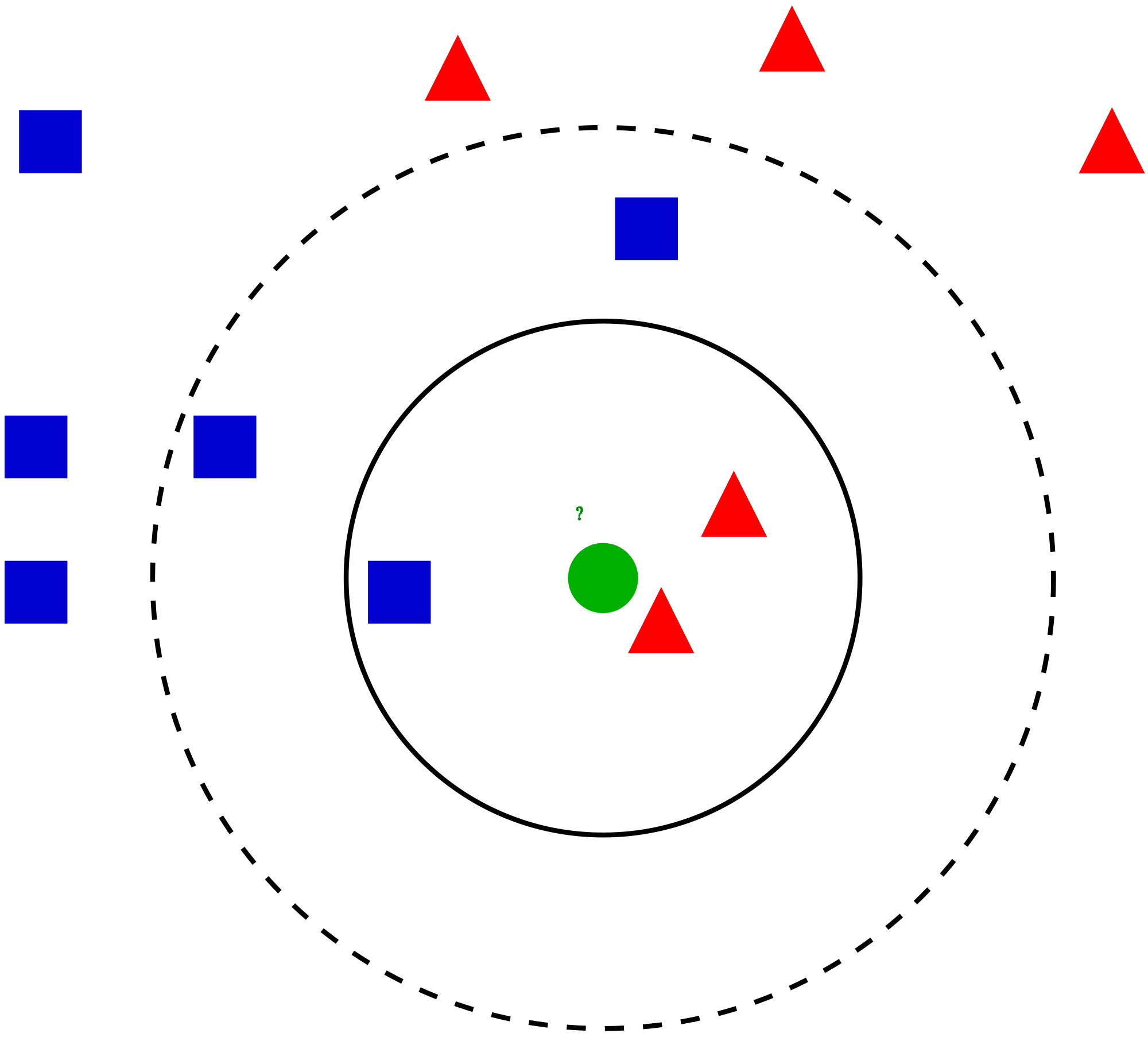
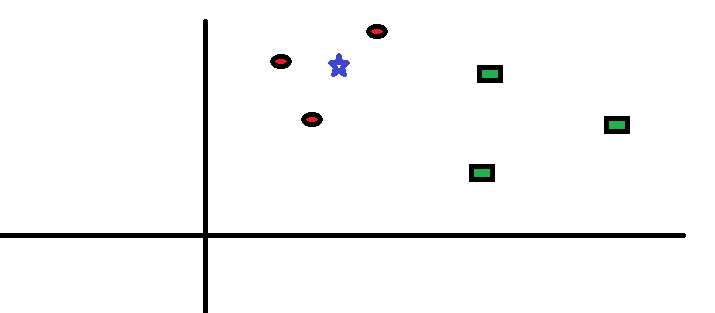
Tomemos un caso sencillo para entender este algoritmo. A continuación se muestra una extensión de círculos rojos (RC) y cuadrados verdes (GS):
Tiene la intención de averiguar la clase de la estrella azul (BS). BS puede ser RC o GS y nada más. El algoritmo «K» es KNN es el vecino más cercano al que deseamos votar. Digamos que K = 3. Por lo tanto, ahora haremos un círculo con BS como centro tan grande como para encerrar solo tres puntos de datos en el plano. Consulte el siguiente diagrama para obtener más detalles:
Los tres puntos más cercanos a BS son todos RC. Por tanto, con un buen nivel de confianza, podemos decir que el BS debería pertenecer a la clase RC. Aquí, la elección se hizo muy obvia ya que los tres votos del vecino más cercano fueron para RC. La elección del parámetro K es muy importante en este algoritmo. A continuación, entenderemos cuáles son los factores a considerar para concluir el mejor K.
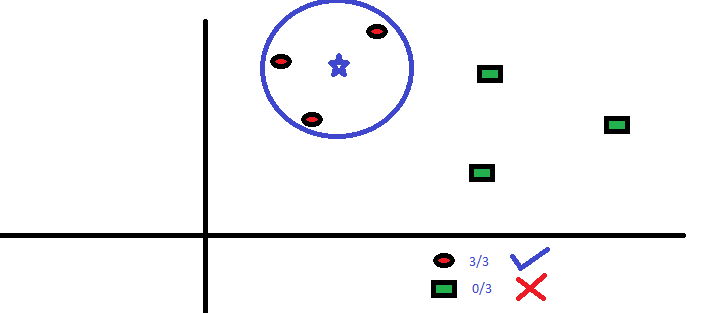
¿Cómo elegimos el factor K?
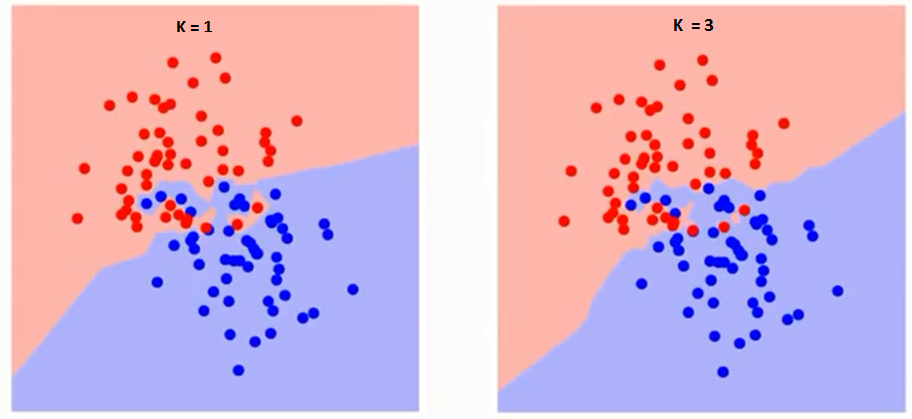
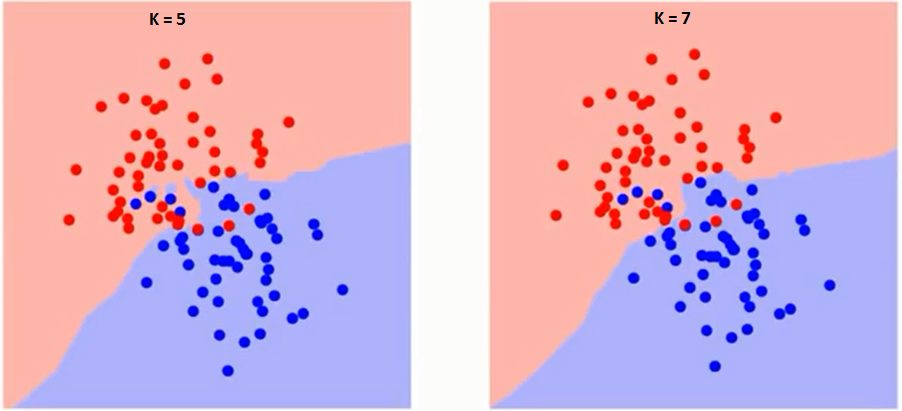
Primero intentemos comprender qué es exactamente lo que influye K en el algoritmo. Si vemos el último ejemplo, dado que las 6 observaciones de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... permanecen constantes, con un valor de K dado podemos establecer límites para cada clase. Estos límites separarán RC de GS. De la misma manera, intentemos ver el efecto del valor «K» en los límites de la clase. Los siguientes son los diferentes límites que separan las dos clases con diferentes valores de K.
Si observa con atención, puede ver que el límite se vuelve más suave al aumentar el valor de K. Con K aumentando hasta el infinito, finalmente se vuelve todo azul o todo rojo, dependiendo de la mayoría total. La tasa de error de entrenamiento y la tasa de error de validación son dos parámetros que necesitamos para acceder a diferentes valores K. A continuación se muestra la curva para la tasa de error de entrenamiento con un valor variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... de K:
Como puede ver, la tasa de error en K = 1 siempre es cero para la muestra de entrenamiento. Esto se debe a que el punto más cercano a cualquier punto de datos de entrenamiento es él mismo, por lo que la predicción siempre es precisa con K = 1. Si la curva de error de validación hubiera sido similar, nuestra elección de K habría sido 1. A continuación se muestra la curva de error de validación con un valor variable de K:
Esto aclara la historia. En K = 1, estábamos sobreajustando los límites. Por tanto, la tasa de error inicialmente disminuye y alcanza un mínimo. Después del punto mínimo, aumenta al aumentar K. Para obtener el valor óptimo de K, puede segregar el entrenamiento y la validación del conjunto de datos inicial. Ahora trace la curva de error de validación para obtener el valor óptimo de K. Este valor de K debe usarse para todas las predicciones.
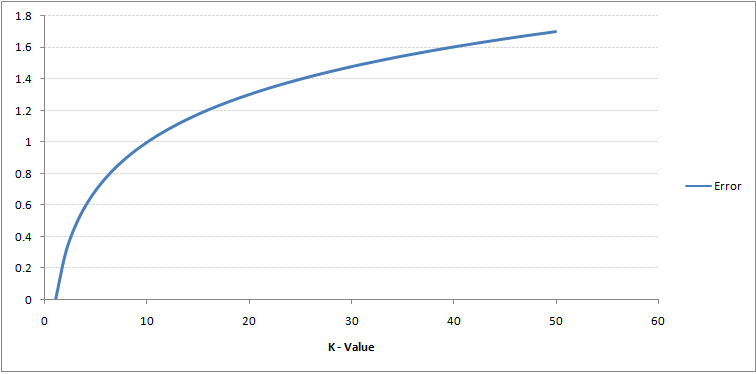
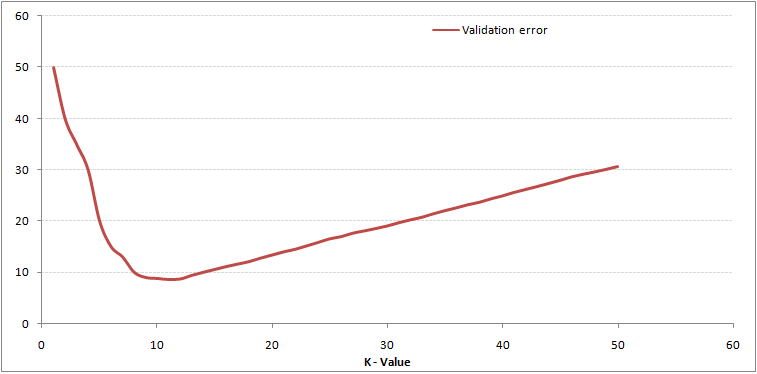
El contenido anterior se puede entender de forma más intuitiva utilizando nuestro curso gratuito: Algoritmo de vecinos más cercanos (KNN) en Python y R
Breaking it Down – Pseudo código de KNN
Podemos implementar un modelo KNN siguiendo los pasos a continuación:
- Cargar los datos
- Inicializar el valor de k
- Para obtener la clase predicha, repita desde 1 hasta el número total de puntos de datos de entrenamiento
- Calcule la distancia entre los datos de prueba y cada fila de datos de entrenamiento. Aquí usaremos la distancia euclidiana como nuestra métrica de distancia, ya que es el método más popular. Las otras métricas que se pueden utilizar son Chebyshev, coseno, etc.
- Ordene las distancias calculadas en orden ascendente según los valores de distancia
- Obtenga las primeras k filas de la matriz ordenada
- Obtenga la clase más frecuente de estas filas
- Devuelve la clase predicha
Implementación en Python desde cero
Usaremos el popular conjunto de datos Iris para construir nuestro modelo KNN. Puedes descargarlo desde aquí.
Comparando nuestro modelo con scikit-learn
from sklearn.neighbors import KNeighborsClassifier neigh = KNeighborsClassifier(n_neighbors=3) neigh.fit(data.iloc[:,0:4], data['Name']) # Predicted class print(neigh.predict(test)) -> ['Iris-virginica'] # 3 nearest neighbors print(neigh.kneighbors(test)[1]) -> [[141 139 120]]
Podemos ver que ambos modelos predijeron la misma clase (‘Iris-virginica’) y los mismos vecinos más cercanos ( [141 139 120] ). Por lo tanto, podemos concluir que nuestro modelo funciona como se esperaba.
Implementación de kNN en R
Paso 1: importar los datos
Paso 2: verificar los datos y calcular el resumen de datos
Producción
#Top observations present in the data SepalLength SepalWidth PetalLength PetalWidth Name 1 5.1 3.5 1.4 0.2 Iris-setosa 2 4.9 3.0 1.4 0.2 Iris-setosa 3 4.7 3.2 1.3 0.2 Iris-setosa 4 4.6 3.1 1.5 0.2 Iris-setosa 5 5.0 3.6 1.4 0.2 Iris-setosa 6 5.4 3.9 1.7 0.4 Iris-setosa #Check the dimensions of the data [1] 150 5 #Summarise the data SepalLength SepalWidth PetalLength PetalWidth Name Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 Iris-setosa :50 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 Iris-versicolor:50 Median :5.800 Median :3.000 Median :4.350 Median :1.300 Iris-virginica :50 Mean :5.843 Mean :3.054 Mean :3.759 Mean :1.199 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800 Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Paso 3: dividir los datos
Paso 4: Calcular la distancia euclidiana
Paso 5: escribir la función para predecir kNN
Paso 6: Cálculo de la etiqueta (Nombre) para K = 1
Producción
For K=1 [1] "Iris-virginica"
De la misma manera, puede calcular otros valores de K.
Comparación de nuestra función de predicción kNN con la biblioteca «Clase»
Producción
For K=1 [1] "Iris-virginica"
Podemos ver que ambos modelos predijeron la misma clase (‘Iris-virginica’).
Notas finales
El algoritmo KNN es uno de los algoritmos de clasificación más simples. Incluso con tanta simplicidad, puede dar resultados altamente competitivos. El algoritmo KNN también se puede utilizar para problemas de regresión. La única diferencia con la metodología discutida será el uso de promedios de los vecinos más cercanos en lugar de votar por los vecinos más cercanos. KNN se puede codificar en una sola línea en R. Todavía tengo que explorar cómo podemos usar el algoritmo KNN en SAS.
¿Le resultó útil el artículo? ¿Ha utilizado alguna otra herramienta de aprendizaje automático recientemente? ¿Planea utilizar KNN en alguno de sus problemas comerciales? Si es así, cuéntenos cómo planea hacerlo.
