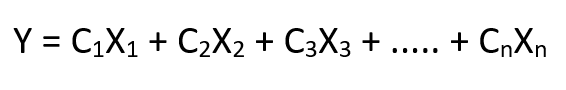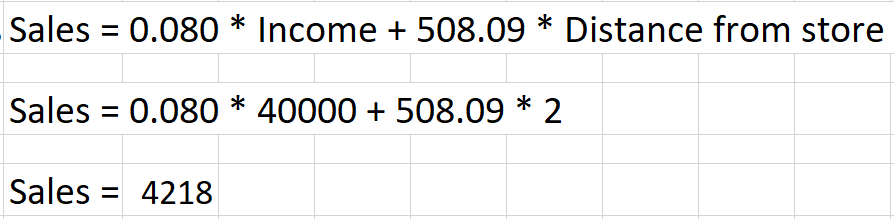Visión general
- Puede realizar modelos predictivos en Excel en solo unos pocos pasos
- Aquí hay un tutorial paso a paso sobre cómo construir un modelo de regresión lineal en Excel y cómo interpretar los resultados.
Introducción
¿Excel para modelado predictivo? ¿En serio?
Por lo general, esa es la primera reacción que obtengo cuando menciono el tema. A esto le sigue una mirada de incredulidad cuando demuestro cómo podemos aprovechar la naturaleza flexible de Excel para construir modelos predictivos para nuestros proyectos de análisis y ciencia de datos.
Déjame hacerte una pregunta: si las tiendas que te rodean comenzaran a recopilar datos de clientes, ¿podrían adoptar una estrategia basada en datos para vender sus productos? ¿Pueden pronosticar sus ventas o estimar la cantidad de productos que podrían venderse?
Ahora debe preguntarse cómo diablos construirán un modelo estadístico complejo que pueda predecir estas cosas. Y aprender análisis o contratar a un analista podría estar más allá de su alcance. Estas son las buenas noticias: no es necesario. Microsoft Excel nos ofrece la capacidad de crear modelos predictivos sin tener que escribir un código complejo que vuela sobre la cabeza de la mayoría de las personas.
Podemos construir fácilmente un modelo simple como la regresión lineal en MS Excel que puede ayudarnos a realizar análisis en unos pocos pasos simples. ¡Y no necesitamos ser un maestro en Excel o Estadística para realizar modelos predictivos!
En este artículo, voy a explicar cómo construir un modelo de regresión lineal en Excel y cómo analizar el resultado para que pueda convertirse en un analista superestrella.
Este es el séptimo artículo de mi serie Excel para analistas. Recomiendo encarecidamente leer los artículos anteriores para convertirse en un analista más eficiente:
Le animo a que consulte los recursos a continuación si es un principiante en Excel y Business Analytics:
Tabla de contenido
- ¿Qué es la regresión lineal?
- Obtener el importantísimo Add Analytics ToolPak en Excel
- Implementación de regresión lineal en Excel
- Interpretación de los resultados de nuestro modelo predictivo
- ¿Cómo podemos mejorar el modelo?
- ¡Haciendo predicciones en Excel!
¿Qué es la regresión lineal?
La regresión lineal es la primera técnica de aprendizaje automático que la mayoría de nosotros aprendemos. También es la técnica de aprendizaje supervisadoEl aprendizaje supervisado es un enfoque de machine learning donde un modelo se entrena utilizando un conjunto de datos etiquetados. Cada entrada en el conjunto de datos está asociada a una salida conocida, lo que permite al modelo aprender a predecir resultados para nuevas entradas. Este método es ampliamente utilizado en aplicaciones como la clasificación de imágenes, el reconocimiento de voz y la predicción de tendencias, destacando su importancia en... más utilizada en la industria.
Pero, ¿qué es la regresión lineal?
Es un enfoque lineal para modelar estadísticamente la relación entre la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente (la variable que desea predecir) y las variables independientes (los factores utilizados para predecir). La regresión lineal nos da una ecuación como esta:
Aquí, tenemos Y como nuestra variable dependiente, las X son las variables independientes y todas las C son los coeficientes. Los coeficientes son básicamente los pesos asignados a las características, en función de su importancia.
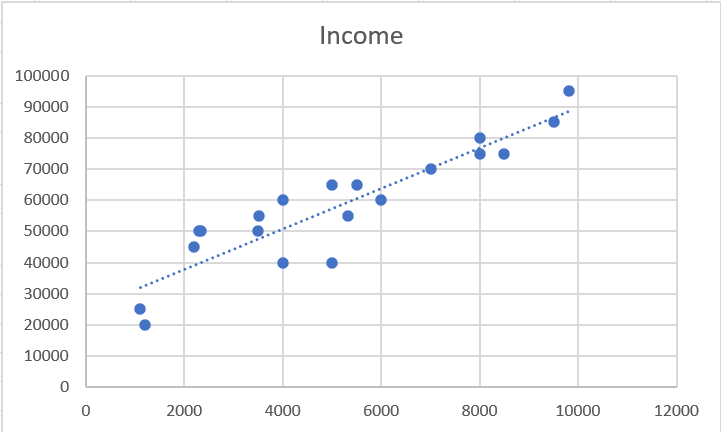
El método más común para realizar la regresión es el OLS (mínimos cuadrados ordinarios). Su objetivo es reducir la suma de cuadrados para producir la línea de mejor ajuste como esta:
Si desea obtener más información sobre la regresión lineal, aquí tiene algunos recursos:
Obtener el Complemento de Excel del All-Important Analysis ToolPack
Para realizar un análisis de regresión en Excel, primero necesitamos habilitar Excel Complemento de herramientas de análisis. Analysis ToolPak en Excel es un programa complementario que proporciona herramientas de análisis de datos para análisis estadístico y de ingeniería.
Para agregarlo en su libro de trabajo, siga estos pasos.
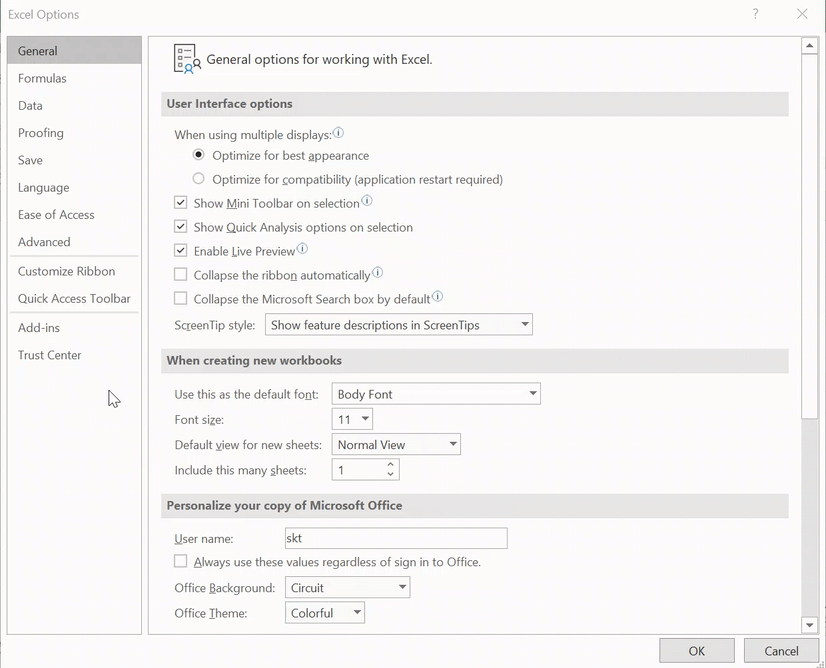
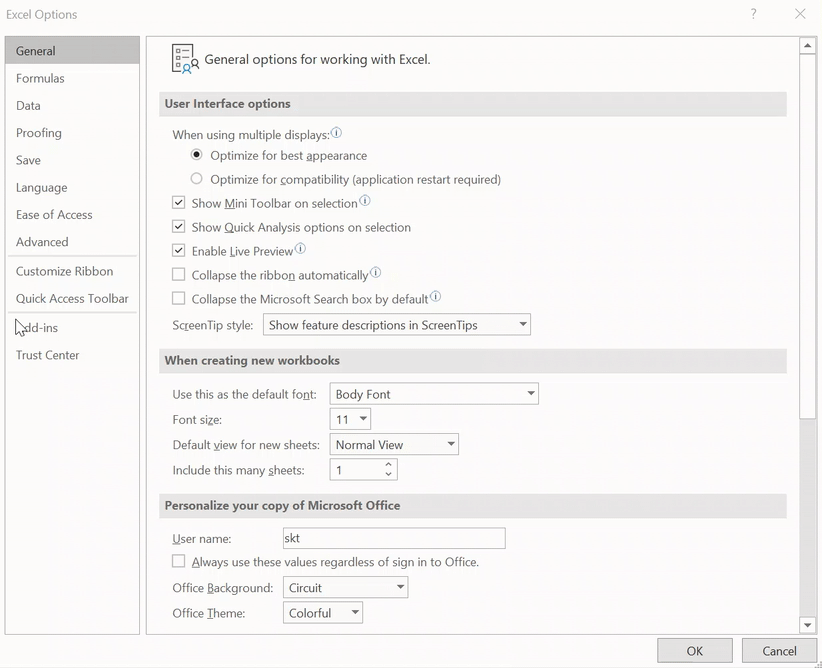
Paso 1 – Opciones de Excel
Ir a Archivos -> Opciones:
Paso 2: ubicar Analytics ToolPak
Ir a Complementos en el panelUn panel es un grupo de expertos que se reúne para discutir y analizar un tema específico. Estos foros son comunes en conferencias, seminarios y debates públicos, donde los participantes comparten sus conocimientos y perspectivas. Los paneles pueden abordar diversas áreas, desde la ciencia hasta la política, y su objetivo es fomentar el intercambio de ideas y la reflexión crítica entre los asistentes.... izquierdo -> Administrar complementos de Excel -> Ir:
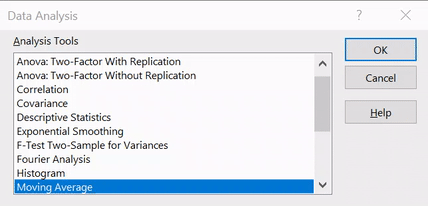
Paso 3: agregue Analytics ToolPak
Selecciona el «Paquete de herramientas de análisis«Y presione OK:
¡Ha agregado con éxito el paquete de herramientas de análisis en Excel! Puedes comprobarlo yendo a la Datos barra en la cinta.
¡Comencemos a construir nuestro modelo predictivo en Excel!
Implementación de regresión lineal en Excel
Muchas cosas eran teóricas hasta ahora. ¡Ahora, profundicemos en Excel y realicemos análisis de regresión lineal!
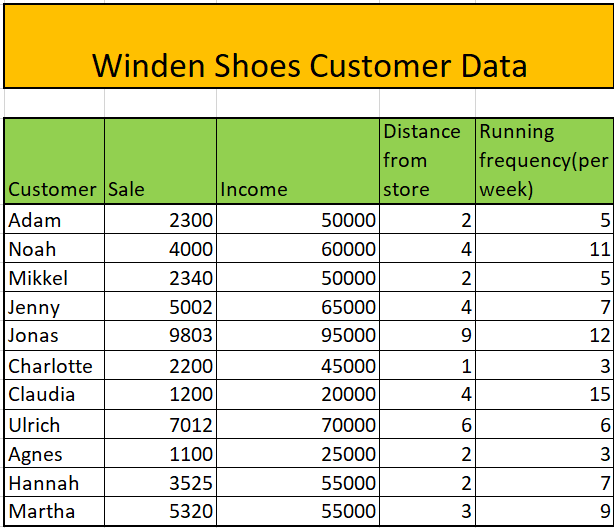
Aquí está la declaración del problema con la que trabajaremos:
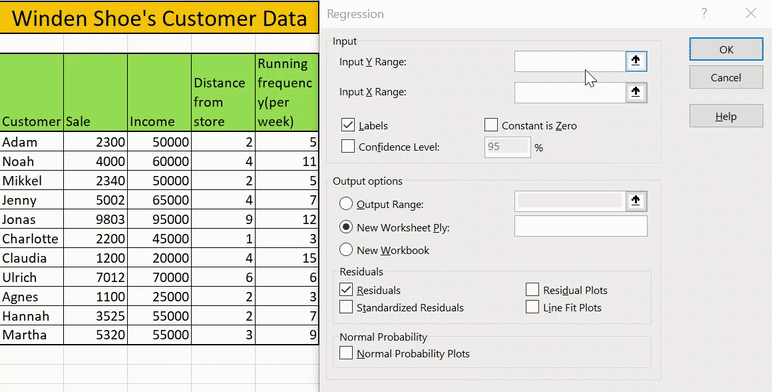
Hay una empresa de venta de zapatos en la ciudad de Winden. La empresa quiere predecir las ventas a través de cada cliente considerando los siguientes factores: ingresos del cliente, distancia de la casa a la tienda, frecuencia de funcionamiento del cliente por semana.
Paso 1: seleccione Regresión
Ir a Datos -> Análisis de los datos:
Vaya a Análisis de datos en el Paquete de herramientas de datos, seleccione Regresión y presione OK:
Paso 2: seleccione Opciones
En este paso, seleccionaremos algunas de las opciones necesarias para nuestro análisis, tales como:
- Rango de entrada y: el rango del factor independiente
- Rango de entrada x: el rango de factores dependientes
- Rango de salida: el rango de celdas donde desea mostrar los resultados.
Las otras opciones son discrecionales y puede seleccionarlas para su propósito específico.
prensa OK ¡y finalmente hemos realizado un análisis de regresión en Excel en solo dos pasos! ¿No fue tan fácil? Ahora veremos el resultado del análisis de regresión en Excel.
Analizando los resultados de nuestro modelo predictivo en Excel
Implementar el modelo de regresión lineal fue la parte fácil. Ahora viene el aspecto complicado de nuestro análisis: interpretar los resultados del modelo predictivo en Excel.
En resumen, tenemos 3 tipos de salida y los cubriremos uno por uno:
- Tabla de estadísticas de regresión
- Tabla ANOVA
- Tabla de coeficientes de regresión
- Tabla residual
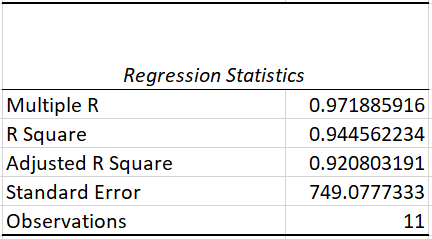
Tabla de estadísticas de regresión
La tabla de estadísticas de regresión nos dice qué tan bien la línea de mejor ajuste define la relación lineal entre las variables independientes y dependientes. Dos de las medidas más importantes son los valores R cuadrado y R cuadrado ajustado.
los R-cuadrado la estadística es el indicador de bondad de ajuste que nos dice cuánta varianza se explica por la línea de mejor ajuste. El valor de R cuadrado varía de 0 a 1. En nuestro caso, tenemos el valor de R cuadrado de 0,953, lo que significa que nuestra línea es capaz de explicar el 95% de la varianza, una buena señal.
Pero hay un problema: a medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... que seguimos agregando más variables, nuestro valor de R cuadrado seguirá aumentando aunque la variable no tenga ningún efecto. R cuadrado ajustado resuelve este problema y es una métrica mucho más confiable.
Tabla ANOVA
ANOVA significa Análisis de varianza. Esta tabla desglosa la suma de cuadrados en sus componentes para dar detalles de la variabilidad dentro del modelo.
Incluye una métrica muy importante, Significado F (o la Valor p), que nos dice si su modelo es estadísticamente significativo o no. En pocas palabras, significa que nuestros resultados probablemente no se deban a la aleatoriedad, sino a una causa subyacente. El umbral más utilizado para el valor p es 0,05. Si obtenemos un valor menor que este, estamos listos para comenzar. De lo contrario, necesitaríamos elegir otro conjunto de variables independientes.
En nuestro caso, tenemos un valor muy por debajo del umbral de 0,05. ¡Genial, podemos seguir adelante ahora!
Tabla de coeficientes de regresión
La tabla de coeficientes desglosa los componentes de la línea de regresión en forma de coeficientes. Podemos entender mucho de estos.
Para la empresa de calzado Winden, parece que por cada unidad de aumento en ingreso, la venta aumenta en 0.08 unidades, y un aumento en una unidad de distancia de la tienda aumenta en 508 unidades!
Parece que un aumento en frecuencia de funcionamiento disminuye las ventas en 24 unidades, pero ¿podemos realmente creer en esta característica? Si miras en la imagen de arriba, notarás que su valor p es mayor que 0.5, lo que significa que no es estadísticamente significativo. Veremos cómo podemos manejar esta situación en la siguiente sección.
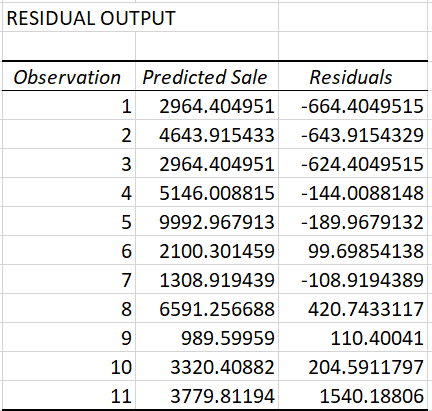
Tabla residual
La tabla residual refleja cuánto varía el valor predicho del valor real. Consiste en los valores predichos por nuestro modelo:
¿Cómo podemos mejorar nuestro modelo?
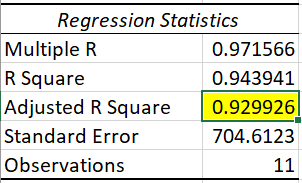
Como vimos anteriormente, el valor p de la variable frecuencia de funcionamiento es más de 0,05, así que comprobemos nuestros resultados eliminando esta variable de nuestro análisis.
Seguiremos todos los pasos mencionados anteriormente pero no incluiremos la columna de frecuencia de ejecución:
¡Observamos que el valor de R-cuadrado ajustado mejoró ligeramente aquí de 0,920 a 0,929!
¡Haciendo predicciones en Excel!
Tenemos el análisis de regresión listo, entonces, ¿qué podemos hacer ahora? Vamos a ver.
Un antiguo cliente suyo llamado Aleksander entra y deseamos predecir las ventas de él. Simplemente podemos ingresar el número de los datos en el modelo de regresión lineal y ¡estamos listos para comenzar!
Aleksander tiene un ingreso de 40k y vive a 2 km de la tienda. ¿Cuáles son las ventas estimadas?
La ecuación se convierte en:
Aquí, nuestro modelo ha estimado que el Sr. Aleksander pagaría 4218 unidades para comprar su nuevo par de zapatos. Ese es el poder de la regresión lineal realizada simplemente en Microsoft Excel.
Notas finales
En este artículo, aprendimos cómo construir un modelo de regresión lineal en Excel y cómo interpretar los resultados. Espero que esta guía le ayude a mejorar como analista o científico de datos.
Analytics ToolPak consta de muchas otras opciones de análisis en Excel. ¡Puedes probar muchos otros análisis estadísticos en tu vida diaria!