Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Introducción
Big Data se refiere a una combinación de datos estructurados y no estructurados que pueden medirse en petabytes o exabytes. Por lo general, utilizamos 3V para caracterizar los 3V de big data, es decir, el volumen de datos, la variedad de tipos de datos y la velocidad a la que se procesan.
Estas tres características dificultan el manejo de macrodatos. Por lo tanto, los macrodatos son costosos en términos de inversión en una gran cantidad de almacenamiento de servidor, sofisticadas máquinas de análisis y metodologías de minería de datos. METROCualquier organización encuentra esto engorroso tanto técnica como económicamente y, por lo tanto, está pensando en cómo lograr Se pueden lograr resultados similares utilizando muchas menos sofisticaciones.. Por lo tanto, están tratando de convertir macrodatos en pequeños datos., que consta de fragmentos de datos utilizables. La siguiente figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... [1] muestra una comparación.
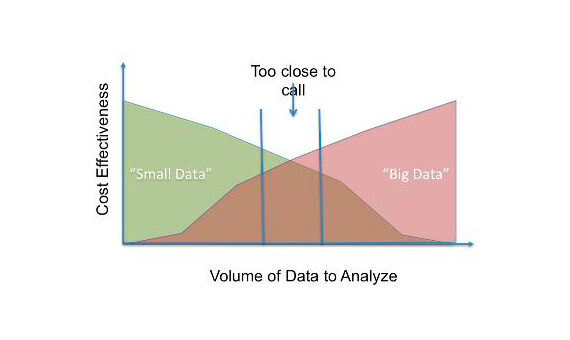
Intentemos explorar una técnica estadística simple, que se puede utilizar para crear una parte utilizable de datos a partir de big data. La muestra, que es básicamente un subconjunto de la población, debe seleccionarse de tal manera que represente adecuadamente a la población. Esto puede garantizarse empleando pruebas estadísticas.
Introducción al muestreo de yacimientos
La idea clave detrás del muestreo de reservorios es crear un ‘reservorio’ a partir de un gran océano de datos. Sea ‘N’ el tamaño de la población y ‘n’ el tamaño de la muestra. Cada elemento de la población tiene la misma probabilidad de estar presente en la muestra y esa probabilidad es (n / N). Con esta idea clave, tenemos que crear una submuestra. Debe tenerse en cuenta que cuando creamos una muestra, las distribuciones deben ser idénticas no solo en filas sino también en columnas.
Por lo general, nos enfocamos solo en las filas, pero también es importante mantener la distribución de las columnas. Las columnas son las características de las que aprende el algoritmo de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina..... Por lo tanto, también tenemos que realizar pruebas estadísticas para cada característica para garantizar que la distribución sea idéntica.
El algoritmo es el siguiente: Inicialice el yacimiento con los primeros ‘n’ elementos de la población de tamaño ‘N’. Luego lea cada fila de su conjunto de datos (i> n). En cada iteración, calcule (n / i). Reemplazamos los elementos del reservorio del siguiente conjunto de ‘n’ elementos con una probabilidad que disminuye gradualmente.
R[i] = S[i]
for i = n+1 to N:
j = U ~ [1, i]
si j <= n:
R[j] = S[i]
Pruebas estadísticas
Como mencioné anteriormente, debemos asegurarnos de que todas las columnas (características) del embalse se distribuyan de manera idéntica a la población. Usaremos la prueba de Kolmogorov-Smirnov para características continuas y la prueba de chi-cuadrado de Pearson para características categóricas.
La prueba de Kolmogorov-Smirnov se utiliza para verificar si las funciones de distribución acumulativa (CDF) de la población y la muestra son las mismas. Comparamos las CDF de la población F_N (x) con el de la muestra F_n (x).
𝐹𝑁𝑥
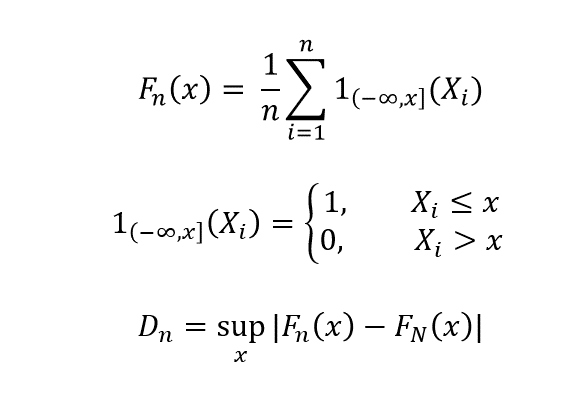
Como n -> N, D_n -> 0, si las distribuciones son idénticas. Esta prueba debe realizarse para todas las características del conjunto de datos que son continuas.
Para las características categóricas, podemos realizar la prueba de chi-cuadrado de Pearson. Sea O_i el número de observaciones de la categoría ‘i’ y ne el número de muestras. Sea E_i el recuento esperado de la categoría ‘i’. Entonces E_i = N p_i, donde p_i es la probabilidad de pertenecer a la categoría ‘i’. Entonces el valor de chi-cuadrado viene dado por la siguiente relación:
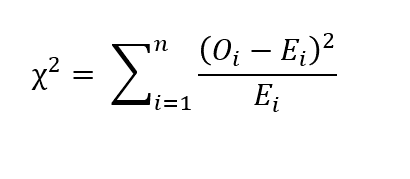
Si chi-cuadrado = 0, eso significa que los valores observados y los valores esperados son los mismos. Si el valor p de la prueba estadística es mayor que el nivel de significancia, decimos que la muestra es estadísticamente significativa.
Notas finales
El muestreo de yacimientos se puede utilizar para crear una parte útil de datos a partir de big data siempre que las dos pruebas, Kolmogorov-Smirnov y chi-cuadrado de Pearson, sean exitosas. Los rumores recientes son, por supuesto, macrodatos. Los modelos centralizados como en la arquitectura de big data vienen acompañados de grandes dificultades. Para descentralizar las cosas y, por lo tanto, hacer que el trabajo sea modular, tenemos que crear pequeños fragmentos de datos útiles y luego obtener información significativa de ellos. Creo que deberían realizarse más esfuerzos en esta dirección, en lugar de invertir en arquitectura para admitir big data.
Referencias
1. https://www.bbvaopenmind.com/en/technology/digital-world/small-data-vs-big-data-back-to-the-basics/






