Big Data

PCA para reducción de dimensionalidad | Dimensiones decrecientes con PCA

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

Introducción

Este artículo le dará claridad sobre qué es la reducción de dimensionalidad, su necesidad y cómo funciona. También hay código Python para ilustración y comparación entre PCA, ICA y t-SNE.

¿Qué es la reducción de dimensionalidad y por qué necesitamos i

Reducción de dimensionalidad es simplemente reducir el número de características (columnas) mientras retiene la máxima información. Las siguientes son razones para la reducción de dimensionalidad:

La reducción de dimensionalidad ayuda en la compresión de datos y, por lo tanto, reduce el espacio de almacenamiento.
Reduce el tiempo de cálculo.
También ayuda a eliminar las funciones redundantes, si las hay.
Elimina las funciones correlacionadas.
Reducir las dimensiones de los datos a 2D o 3D puede permitirnos trazarlos y visualizarlos con precisión. A continuación, puede observar patrones con mayor claridad.
También es útil para eliminar el ruido y, como resultado de eso, podemos mejorar

Hay muchos métodos para la reducción de dimensionalidad como PCA, ICA, t-SNE, etc., veremos PCA (Análisis de componentes principales).

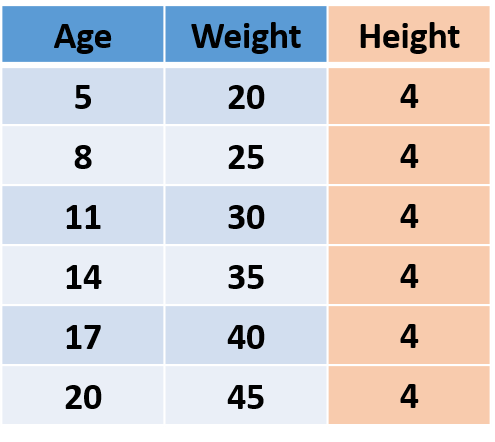
Primero entendamos lo que es información en datos. Considere los siguientes datos imaginarios, que tienen la edad, el peso y la altura de las personas.

Como la ‘Altura’ de todas las personas es la misma, es decir, la varianza es 0, por lo que no agrega ninguna información, por lo que podemos eliminar la columna ‘Altura’ sin perder ninguna información.

Ahora que sabemos que la información es varianza, entendamos el funcionamiento de PCA. En PCA, encontramos nuevas dimensiones (características) que capturan la varianza máxima (es decir, información). Para entender esto usaremos el ejemplo anterior. Después de eliminar ‘Altura’, nos queda ‘Edad’ y ‘Peso’. Estas dos características están cuidando toda la información. En otras palabras, podemos decir que necesitamos 2 características (Edad y Altura) para contener la información, y si podemos encontrar una nueva característica que por sí sola pueda contener toda la información, podemos reemplazar las características de origen 2 con una nueva característica única, logrando reducción de dimensionalidad!

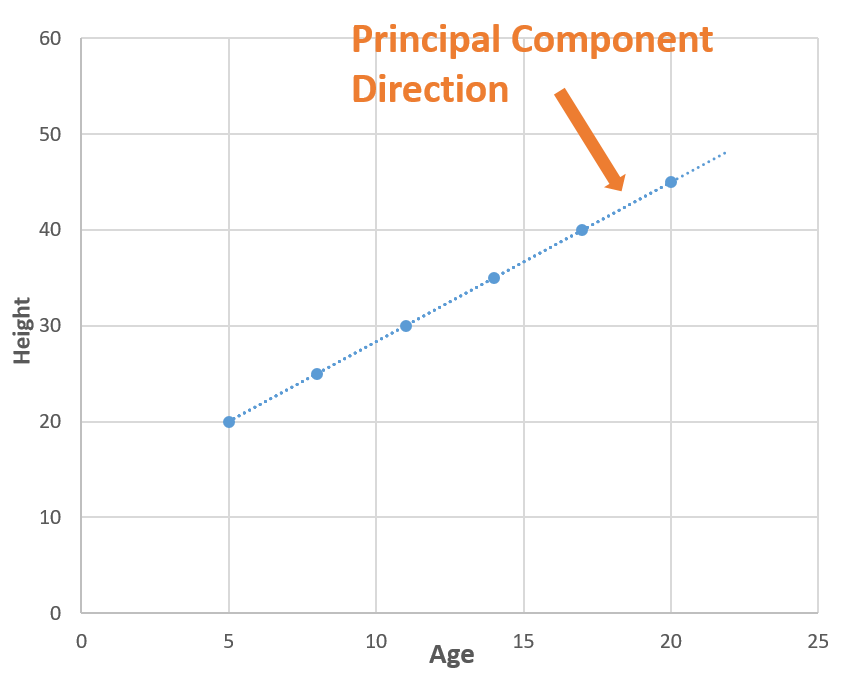
Ahora considere una línea (línea punteada azul) que pasa por todos los puntos. La línea de puntos azul está capturando toda la información, por lo que podemos reemplazar ‘Edad’ y ‘Peso’ (2 dimensiones) con la línea de puntos azul (1 dimensión"Dimensión" es un término que se utiliza en diversas disciplinas, como la física, la matemática y la filosofía. Se refiere a la medida en la que un objeto o fenómeno puede ser analizado o descrito. En física, por ejemplo, se habla de dimensiones espaciales y temporales, mientras que en matemáticas puede referirse a la cantidad de coordenadas necesarias para representar un espacio. Su comprensión es fundamental para el estudio y...) sin perder ninguna información, y en este w

Te preguntarás cómo encontramos la línea de puntos azul (componente principal), por lo que hay muchas matemáticas detrás de ella.. Puedes leer Este artículo lo que explica esto, pero en palabras simples, encontramos las direcciones en las que podemos capturar la varianza máxima utilizando valores propios y vectores propios.

Ilustración de PCA en Python

Veamos cómo usar PCA con un ejemplo. He utilizado datos de calidad del vino que tienen 12 características como acidez, azúcar residual, cloruros, etc., y la calidad del vino para 1600 muestras. Puede descargar el cuaderno jupyter de aquí y síguelo.

Primero, carguemos los datos.

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA

df = pd.read_csv('winequality-red.csv')
df.head()
y = df.pop('quality')

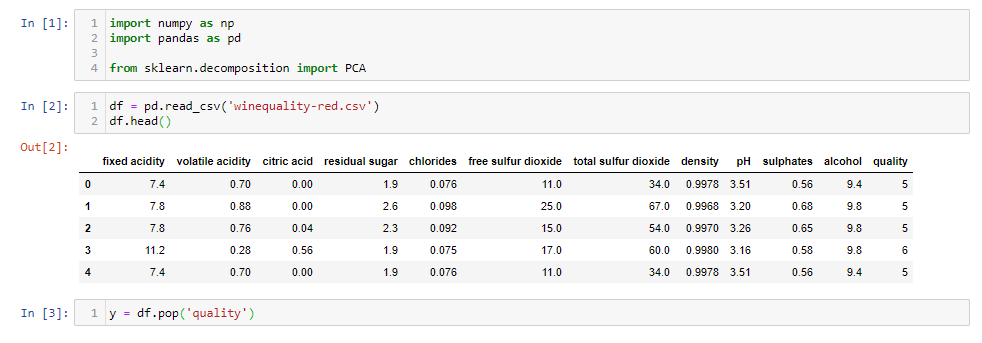
Después de cargar los datos, eliminamos la ‘Calidad’ del vino, ya que es la característica de destino. Ahora escalaremos los datos porque si no, PCA no podrá encontrar los Componentes Principales óptimos. Por ej. tenemos una característica en ‘metros’ y otra en ‘kilómetros’, la característica con unidad ‘metro’ tendrá más varianza que ‘kilómetros’ (1 km = 1000 m), por lo que PCA le dará más importancia a la característica con alta varianza . Entonces, hagamos la escala.

from sklearn.preprocessing import StandardScaler
scalar = StandardScaler()
df_scaled = pd.DataFrame(scalar.fit_transform(df), columns=df.columns)
df_scaled

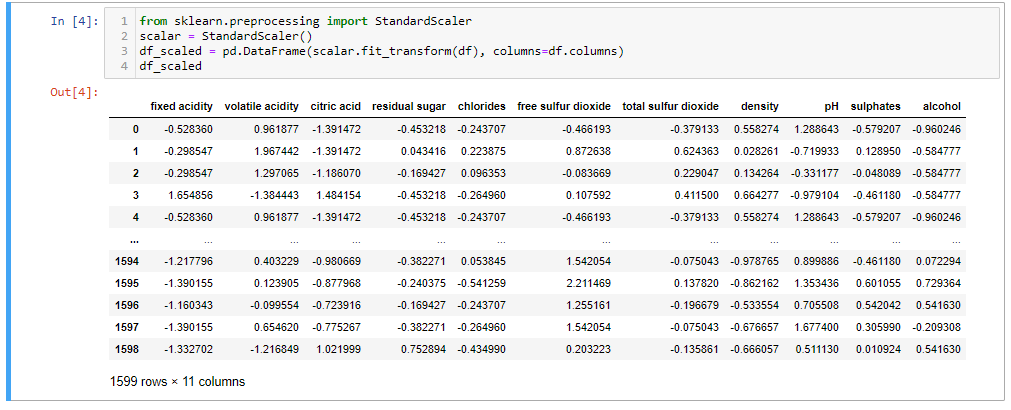
Ahora nosotros

pca = PCA()
df_pca = pd.DataFrame(pca.fit_transform(df_scaled))
df_pca

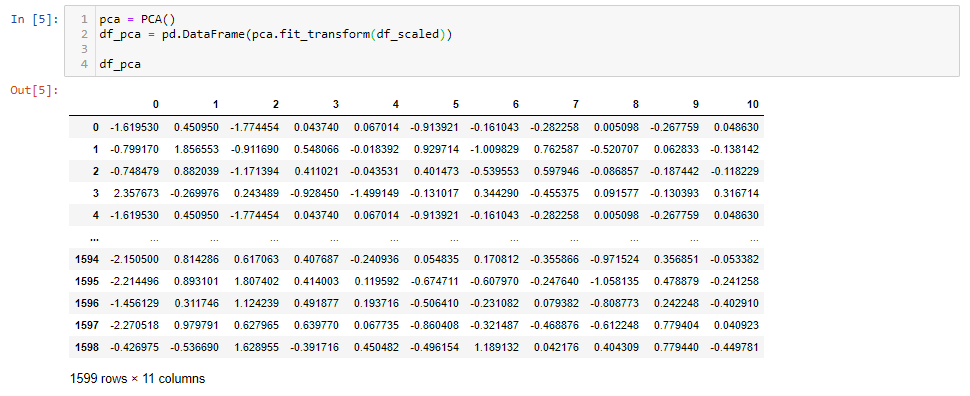
Después de aplicar PCA, obtuvimos 11 componentes principales. Es interesante ver cuánta varianza captura cada componente principal.

import matplotlib.pyplot as plt
pd.DataFrame(pca.explained_variance_ratio_).plot.bar()
plt.legend('')
plt.xlabel('Principal Components')
plt.ylabel('Explained Varience');

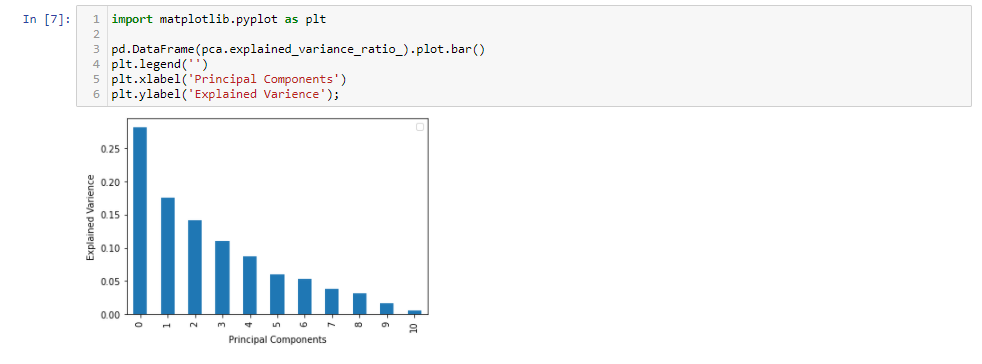
Los primeros 5 componentes principales capturan alrededor del 80% de la varianza, por lo que podemos reemplazar las 11 características originales (acidez, azúcar residual, cloruros, etc.) con las nuevas 5 características que tienen el 80% de la información. Por lo tanto, hemos reducido las 11 dimensiones a solo 5 dimensiones, conservando la mayor parte de la información.

Diferencia entre PCA, ICA y t-SNE

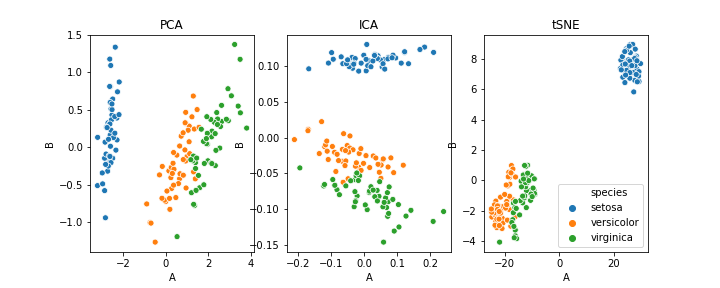
Como este artículo se centra en las ideas básicas detrás de la reducción de dimensionalidad y el funcionamiento de PCA, no entraremos en detalles, pero aquellos que estén interesados pueden pasar por Este artículo.

En resumen, PCA reduce la dimensionalidad mientras captura la mayor parte de la varianza. Ahora, estaría emocionado de aplicar PCA a sus datos, pero antes de eso, quiero resaltar algunas de las desventajas de PCA: