¿Qué es el aprendizaje profundo? Tutorial sobre aprendizaje profundo

Este artículo fue publicado como parte del Blogatón de ciencia de datos.

La guía es principalmente para principiantes, y trataré de definir y enfatizar los temas tanto como pueda. Dado que el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud... es un tema muy grande, dividiría todo el tutorial en pocas partes. Asegúrese de leer las otras partes si encuentra útil esta.

Contenido

1. Introducción

• ¿Qué es el aprendizaje profundo?
• ¿Por qué Deep Learning?
• ¿Qué cantidad de datos es grande?
• Campos donde se utiliza el aprendizaje profundo
• Diferencia entre Deep Learning y Machine Learning

2) Importar las bibliotecas necesarias

3) Resumen

4) Regresión logística

• Grafo computacional
• Inicializando parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto....
• Propagación hacia adelante
• Optimización con Gradient Descent

5) Regresión logística con Sklearn

6) Notas finales

Introducción

¿Qué es el aprendizaje profundo?

• Es un subcampo del aprendizaje automático, inspirado en las neuronas biológicas del cerebro y traduciéndolo a redes neuronales artificiales con aprendizaje de representación.

¿Por qué el aprendizaje profundo?

• Cuando aumenta el volumen de datos, las técnicas de aprendizaje automático, sin importar cuán optimizadas sean, comienzan a volverse ineficientes en términos de rendimiento y precisión, mientras que el aprendizaje profundo funciona mucho mejor en tales casos.

¿Qué cantidad de datos es grande?

• Bueno, no se puede cuantificar un umbral para que los datos se consideren grandes, pero, intuitivamente, digamos que una muestra de un millón podría ser suficiente para decir «Es grande» (aquí es donde Michael Scott habría pronunciado sus famosas palabras «Eso es lo que ella dijo»).

Campos donde se usa DL

• Clasificación de imágenes, reconocimiento de voz, PNL (procesamiento del lenguaje natural), sistemas de recomendación, etc.

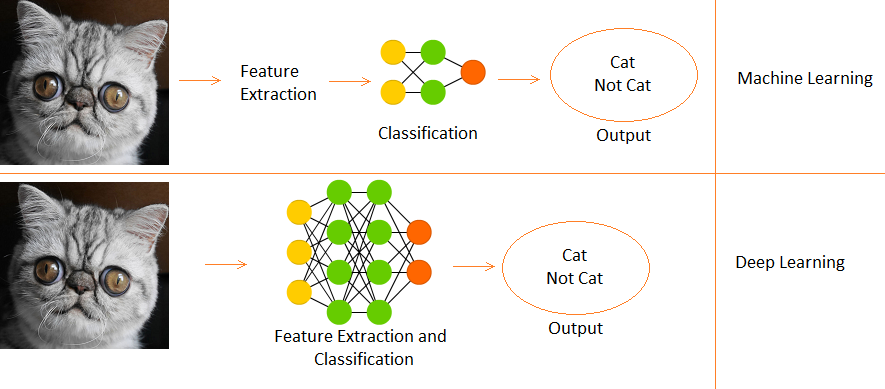
Diferencia entre aprendizaje profundo y aprendizaje automático

• El aprendizaje profundo es un subconjunto del aprendizaje automático.
• En Machine Learning, las funciones se proporcionan manualmente.
• Mientras que Deep Learning aprende funciones directamente de los datos.

Usaremos el Conjunto de datos de dígitos en lenguaje de señas que está disponible en Kaggle aquí. Ahora comencemos.

Importación de bibliotecas necesarias

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib.pyplot as plt
# Input data files are available in the "../input/" directory.
# import warnings
import warnings
# filter warnings
warnings.filterwarnings('ignore')
from subprocess import check_output
print(check_output(["ls", "../input"]).decode("utf8"))
# Any results you write to the current directory are saved as output.

Resumen de los datos

• Hay 2062 imágenes de dígitos en lenguaje de señas en este conjunto de datos.
• Dado que hay 10 dígitos del 0 al 9, hay 10 imágenes de señales únicas.
• Al principio, solo usaremos 0 y 1 (para que sea simple para los estudiantes)
• En los datos, el signo de la mano para 0 está entre los índices 204 y 408. Hay 205 muestras para 0.
• Además, el signo de la mano para 1 está entre los índices 822 y 1027. Hay 206 muestras.
• Por lo tanto, usaremos 205 muestras de cada clase (Nota: en realidad, 205 muestras son mucho menos para un modelo de Deep Learning adecuado, pero como se trata de un tutorial, podemos ignorarlo),

Ahora prepararemos nuestras matrices X e Y, donde X es nuestra matriz de imágenes (características) e Y es nuestra matriz de etiquetas (0 y 1).

# load data set
x_l = np.load('../input/Sign-language-digits-dataset/X.npy')
Y_l = np.load('../input/Sign-language-digits-dataset/Y.npy')
img_size = 64
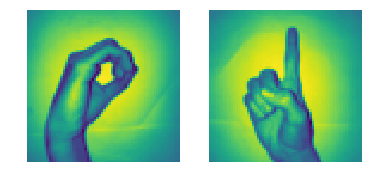
plt.subplot(1, 2, 1)
plt.imshow(x_l[260].reshape(img_size, img_size))
plt.axis('off')
plt.subplot(1, 2, 2)
plt.imshow(x_l[900].reshape(img_size, img_size))
plt.axis('off')

# Join a sequence of arrays along an row axis.
# from 0 to 204 is zero sign and from 205 to 410 is one sign
X = np.concatenate((x_l[204:409], x_l[822:1027] ), axis=0)
z = np.zeros(205)
o = np.ones(205)
Y = np.concatenate((z, o), axis=0).reshape(X.shape[0],1)
print("X shape: " , X.shape)
print("Y shape: " , Y.shape)

Para crear nuestra matriz X, primero dividimos y concatenamos nuestros segmentos de imágenes de signos de mano de 0 y 1 del conjunto de datos a la matriz X. A continuación, hacemos algo similar con Y, pero usamos las etiquetas en su lugar.

1) Entonces vemos que la forma de nuestra matriz X es (410, 64, 64)

• El 410 significa 205 imágenes de 0, 205 imágenes de 1.
• el 64 significa que el tamaño de nuestras imágenes es de 64 x 64 píxeles.

2) La forma de Y es (410,1), por lo tanto, 410 unos y ceros.

3) Ahora dividimos X e Y en trenes y conjuntos de prueba.

• tren = 75%, tren = 15%
• random_state = Utiliza una semilla en particular mientras se aleatoriza, por lo tanto, si la celda se ejecuta varias veces, el número aleatorio generado no cambia cada vez. La misma distribución de prueba y tren se crea cada vez.

# Then lets create x_train, y_train, x_test, y_test arrays
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.15, random_state=42)
number_of_train = X_train.shape[0]
number_of_test = X_test.shape[0]

Tenemos una matriz de entrada tridimensional, por lo que tenemos que aplanarla a 2D para alimentar nuestro primer modelo de aprendizaje profundo. Como y ya es 2D, lo dejamos tal como está.

X_train_flatten = X_train.reshape(number_of_train,X_train.shape[1]*X_train.shape[2])
X_test_flatten = X_test .reshape(number_of_test,X_test.shape[1]*X_test.shape[2])
print("X train flatten",X_train_flatten.shape)
print("X test flatten",X_test_flatten.shape)

Ahora tenemos un total de 348 imágenes, cada una con 4096 píxeles en la matriz de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... X. Y 62 imágenes de la misma densidad de píxeles 4096 en la matriz de prueba. Ahora transponemos las matrices. Esta es solo una elección personal y verá en los próximos códigos por qué lo digo.

x_train = X_train_flatten.T
x_test = X_test_flatten.T
y_train = Y_train.T
y_test = Y_test.T
print("x train: ",x_train.shape)
print("x test: ",x_test.shape)
print("y train: ",y_train.shape)
print("y test: ",y_test.shape)

Así que ahora hemos terminado con la preparación de nuestros datos requeridos. Así es como se ve:

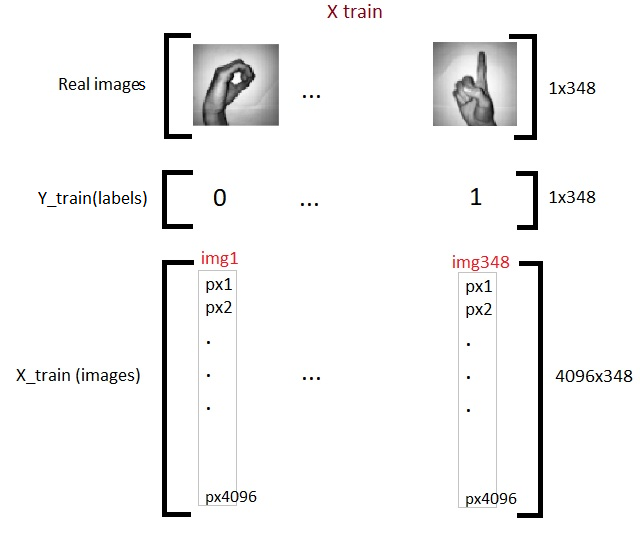
Ahora nos familiarizaremos con uno de los modelos básicos de Dl, llamado Regresión logística.

Regresión logística

Cuando se habla de clasificación binaria, el primer modelo que me viene a la mente es la regresión logística. Pero uno podría preguntarse ¿cuál es el uso de la regresión logística en el aprendizaje profundo? La respuesta es simple, ya que la regresión logística es una red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... simple. Los términos red neuronal y aprendizaje profundo van de la mano. Para comprender la regresión logística, primero tenemos que aprender acerca de las gráficas computacionales.

Gráfico de cálculo

Los gráficos computacionales pueden considerarse una forma pictórica de representar expresiones matemáticas. Entendamos eso con un ejemplo. Supongamos que tenemos una expresión matemática simple como:

c = ( a² + b² ) ^1/2

Su gráfico computacional será:

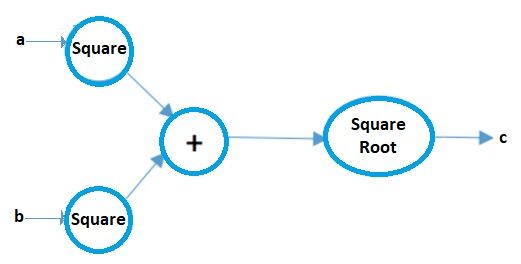
Fuente de la imagen: Autor

Ahora veamos un gráfico computacional de regresión logística:

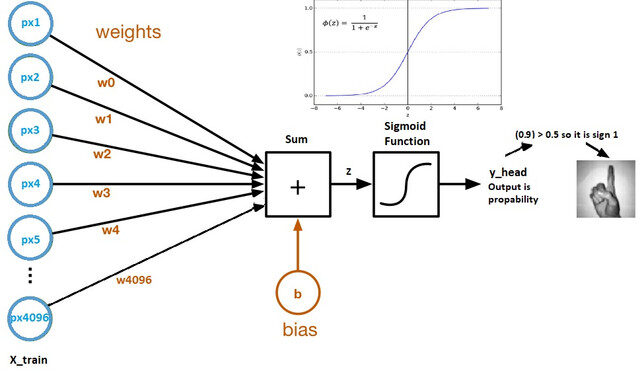
Fuente de la imagen: conjunto de datos de Kaggle

• Los pesos y el sesgo se denominan parámetros del modelo.
• Los pesos representan los coeficientes de cada píxel.
• El sesgo es la intersección de la curva formada al trazar parámetros frente a etiquetas.
• Z = (px1 * wx1) + (px2 * wx2) +…. + (px4096 * wx4096)
• y_head = sigmoid_funtion (Z)
• Lo que hace la función sigmoidea es esencialmente escalar el valor de Z entre 0 y 1, por lo que se convierte en una probabilidad.

¿Por qué utilizar la función sigmoidea?

• Nos da un resultado probabilístico.
• Dado que es un derivado, podemos usarlo en el algoritmo de descenso de gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en....

Ahora examinaremos en detalle cada uno de los componentes del gráfico computacional anterior.

Parámetros de inicialización

Fuente de imagen: Documentos de Microsoft

Cada píxel tiene su propio peso. Pero la pregunta es ¿cuáles serán sus pesos iniciales? Hay varias técnicas para hacer eso que cubriré en la parte 2 de este artículo, pero por ahora, podemos inicializarlas usando cualquier valor aleatorio, digamos 0.01.

La forma de la matriz de pesos será (4096, 1), ya que hay un total de 4096 píxeles por imagen, y deje que el sesgo inicial sea 0.

# lets initialize parameters
# So what we need is dimension 4096 that is number of pixels as a parameter for our initialize method(def)
def initialize_weights_and_bias(dimension):
    w = np.full((dimension,1),0.01)
    b = 0.0
    return w, b

w,b = initialize_weights_and_bias(4096)

Propagación hacia adelante

Todos los pasos desde los píxeles hasta la función de coste se denominan propagación hacia adelante.

Para calcular Z usamos la fórmula: Z = (wT) x + b. donde x es la matriz de píxeles, w pesos y b es el sesgo. Después de calcular Z, lo introducimos en la función sigmoidea que devuelve y_head (probabilidad). Después de eso, calculamos la función de pérdidaLa función de pérdida es una herramienta fundamental en el aprendizaje automático que cuantifica la discrepancia entre las predicciones del modelo y los valores reales. Su objetivo es guiar el proceso de entrenamiento al minimizar esta diferencia, permitiendo así que el modelo aprenda de manera más efectiva. Existen diferentes tipos de funciones de pérdida, como el error cuadrático medio y la entropía cruzada, cada una adecuada para distintas tareas y... (error).

La función de costo es la suma de todas las pérdidas y penaliza al modelo por las predicciones incorrectas. Así es como nuestro modelo aprende los parámetros.

# calculation of z
#z = np.dot(w.T,x_train)+b
def sigmoid(z):
    y_head = 1/(1+np.exp(-z))
    return y_head

y_head = sigmoid(0)
y_head
> 0.5

La expresión matemática de la función de pérdida (log) es:

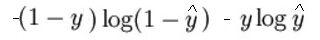
Como dije anteriormente, lo que esencialmente hace la función de pérdida es penalizar las predicciones incorrectas. aquí está el código para la propagación hacia adelante:

# Forward propagation steps:
# find z = w.T*x+b
# y_head = sigmoid(z)
# loss(error) = loss(y,y_head)
# cost = sum(loss)
def forward_propagation(w,b,x_train,y_train):
    z = np.dot(w.T,x_train) + b
    y_head = sigmoid(z) # probabilistic 0-1
    loss = -y_train*np.log(y_head)-(1-y_train)*np.log(1-y_head)
    cost = (np.sum(loss))/x_train.shape[1]      # x_train.shape[1]  is for scaling
    return cost

Optimización con Gradient Descent

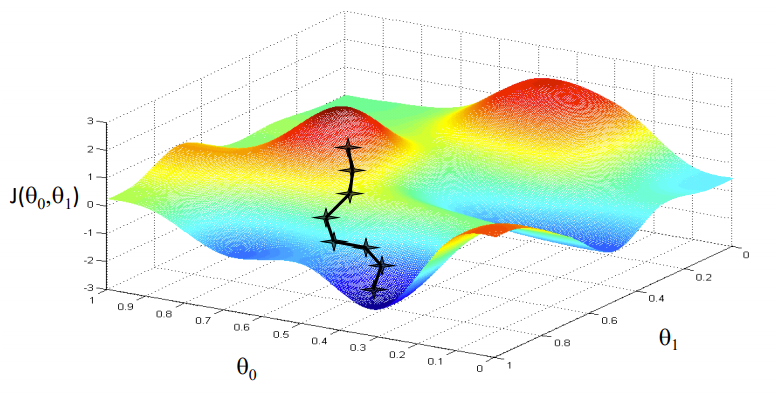
Fuente de la imagen: Coursera

Nuestro objetivo es encontrar los valores de nuestros parámetros para los cuales, la función de pérdida es el mínimo. La ecuación para el descenso de gradientes es:

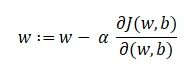
Donde w es el peso o el parámetro. La letra griega alfa es algo llamado tamaño escalonado. Lo que significa es el tamaño de las iteraciones que tomaremos mientras bajamos la pendiente para encontrar los mínimos locales. Y el resto es la derivada de la función de pérdida, también conocida como gradiente. El algoritmo para el descenso de gradientes es simple:

1. Primero, tomamos un punto de datos aleatorio en nuestro gráfico y encontramos su pendiente.
2. Luego encontramos la dirección en la que disminuye la función de pérdida de valor.
3. Actualice los pesos usando la fórmula anterior. (Este método también se llama retropropagación)
4. Seleccione el siguiente punto tomando un tamaño de α.
5. Repetir.

# In backward propagation we will use y_head that found in forward progation
# Therefore instead of writing backward propagation method, lets combine forward propagation and backward propagation
def forward_backward_propagation(w,b,x_train,y_train):
    # forward propagation
    z = np.dot(w.T,x_train) + b
    y_head = sigmoid(z)
    loss = -y_train*np.log(y_head)-(1-y_train)*np.log(1-y_head)
    cost = (np.sum(loss))/x_train.shape[1]      # x_train.shape[1]  is for scaling
    # backward propagation
    derivative_weight = (np.dot(x_train,((y_head-y_train).T)))/x_train.shape[1] # x_train.shape[1]  is for scaling
    derivative_bias = np.sum(y_head-y_train)/x_train.shape[1]                 # x_train.shape[1]  is for scaling
    gradients = {"derivative_weight": derivative_weight,"derivative_bias": derivative_bias}
    return cost,gradients

Ahora actualizamos los parámetros de aprendizaje:

# Updating(learning) parameters
def update(w, b, x_train, y_train, learning_rate,number_of_iterarion):
    cost_list = []
    cost_list2 = []
    index = []
    # updating(learning) parameters is number_of_iterarion times
    for i in range(number_of_iterarion):
        # make forward and backward propagation and find cost and gradients
        cost,gradients = forward_backward_propagation(w,b,x_train,y_train)
        cost_list.append(cost)
        # lets update
        w = w - learning_rate * gradients["derivative_weight"]
        b = b - learning_rate * gradients["derivative_bias"]
        if i % 10 == 0:
            cost_list2.append(cost)
            index.append(i)
            print ("Cost after iteration %i: %f" %(i, cost))
    # we update(learn) parameters weights and bias
    parameters = {"weight": w,"bias": b}
    plt.plot(index,cost_list2)
    plt.xticks(index,rotation='vertical')
    plt.xlabel("Number of Iterarion")
    plt.ylabel("Cost")
    plt.show()
    return parameters, gradients, cost_list

parameters, gradients, cost_list = update(w, b, x_train, y_train, learning_rate = 0.009,number_of_iterarion = 200)

Hasta este punto, aprendimos nuestros parámetros. Significa que estamos ajustando los datos. En el paso de predicción, tenemos x_test como entrada y usándolo, hacemos predicciones hacia adelante.

 # prediction
def predict(w,b,x_test):
    # x_test is a input for forward propagation
    z = sigmoid(np.dot(w.T,x_test)+b)
    Y_prediction = np.zeros((1,x_test.shape[1]))
    # if z is bigger than 0.5, our prediction is sign one (y_head=1),
    # if z is smaller than 0.5, our prediction is sign zero (y_head=0),
    for i in range(z.shape[1]):
        if z[0,i]<= 0.5:
            Y_prediction[0,i] = 0
        else:
            Y_prediction[0,i] = 1

    return Y_prediction

predict(parameters["weight"],parameters["bias"],x_test)

Ahora hacemos nuestras predicciones. Pongámoslo todo junto:

def logistic_regression(x_train, y_train, x_test, y_test, learning_rate ,  num_iterations):
    # initialize
    dimension =  x_train.shape[0]  # that is 4096
    w,b = initialize_weights_and_bias(dimension)
    # do not change learning rate
    parameters, gradients, cost_list = update(w, b, x_train, y_train, learning_rate,num_iterations)
    
    y_prediction_test = predict(parameters["weight"],parameters["bias"],x_test)
    y_prediction_train = predict(parameters["weight"],parameters["bias"],x_train)

    # Print train/test Errors
    print("train accuracy: {} %".format(100 - np.mean(np.abs(y_prediction_train - y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(y_prediction_test - y_test)) * 100))
    
logistic_regression(x_train, y_train, x_test, y_test,learning_rate = 0.01, num_iterations = 150)

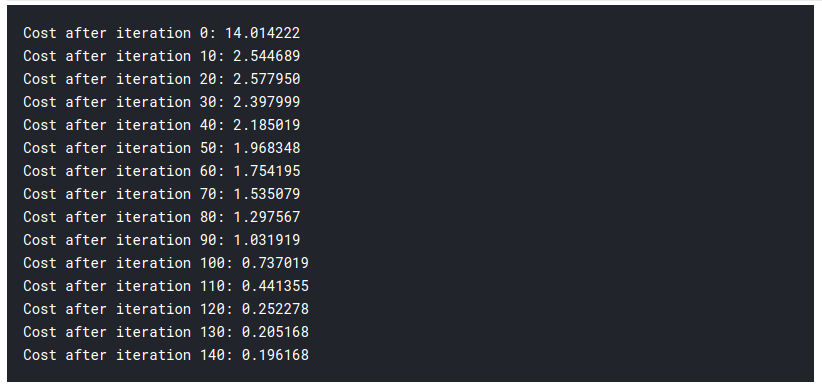
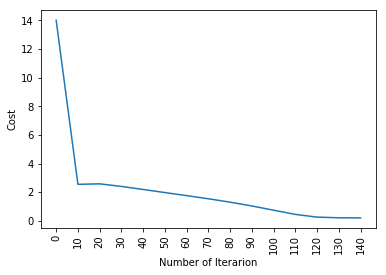
Entonces, como puede ver, incluso el modelo más fundamental de aprendizaje profundo es bastante difícil. No es fácil para ti aprender, y los principiantes a veces pueden sentirse abrumados al estudiar todo esto de una vez. Pero la cuestión es que aún no hemos tocado el aprendizaje profundo, esto es como la superficie. Hay mucho más que agregaré en la parte 2 de este artículo.

Dado que hemos aprendido la lógica detrás de la regresión logística, podemos usar una biblioteca llamada SKlearn que ya tiene muchos de los modelos y algoritmos incorporados, por lo que no tiene que comenzar todo desde cero.

Regresión logística con Sklearn

No voy a explicar mucho en esta sección ya que conoces casi toda la lógica y la intuición detrás de la regresión logística. Si está interesado en leer sobre la biblioteca de Sklearn, puede leer la documentación oficial aquí. Aquí está el código, y estoy seguro de que se quedará atónito al ver el poco esfuerzo que requiere:

from sklearn import linear_model
logreg = linear_model.LogisticRegression(random_state = 42,max_iter= 150)
print("test accuracy: {} ".format(logreg.fit(x_train.T, y_train.T).score(x_test.T, y_test.T)))
print("train accuracy: {} ".format(logreg.fit(x_train.T, y_train.T).score(x_train.T, y_train.T)))

¡Sí! esto es todo lo que se necesitó, ¡solo 1 línea de código!

Notas finales

Hemos aprendido mucho hoy. Pero esto es solo el principio. Asegúrese de consultar la parte 2 de este artículo. Puede encontrarlo en el siguiente enlace. Si le gusta lo que lee, puede leer algunos de los otros artículos interesantes que he escrito.

Sion | Autor en DataPeaker

Espero que hayas pasado un buen rato leyendo mi artículo. ¡¡Salud!!

Los medios que se muestran en este artículo sobre las principales bibliotecas de aprendizaje automático en Julia no son propiedad de DataPeaker y se utilizan a discreción del autor.

Relacionado