Este artículo fue publicado como parte del Blogatón de ciencia de datos.
Advertencia: este artículo es para principiantes absolutos, supongo que acaba de ingresar al campo del aprendizaje automático con algunos conocimientos de matemáticas de la escuela secundaria y algo de codificación básica, pero eso ni siquiera es obligatorio.
Introducción
La regresión lineal es el algoritmo de aprendizaje automático supervisado más básico. Supervise en el sentido de que el algoritmo puede responder su pregunta basándose en datos etiquetados que usted alimenta al algoritmo. La respuesta sería como predecir los precios de la vivienda, clasificar perros frente a gatos. Aquí vamos a hablar de una tarea de regresión usando Regresión lineal. Al final, vamos a predecir los precios de la vivienda en función del área de la casa.
No quiero aburrirlos lanzando todas las palabras de la jerga del aprendizaje automático, al principio, así que permítanme comenzar con la ecuación lineal más básica. (y = mx + b) que todos conocemos desde nuestra época escolar.
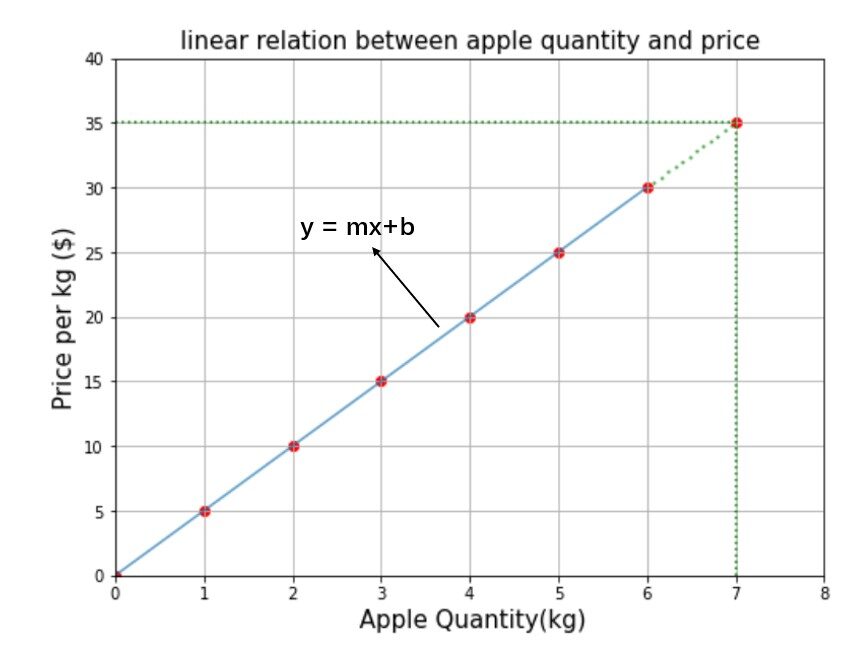
La figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... anterior muestra la relación entre la cantidad de manzana y el precio de costo. ¿Cuánto tienes que pagar por 7 kg de manzanas? Sé que es fácil. Si 1 kg cuesta 5 $, entonces 7 kg cuestan 7 * 5 = 35 $ o simplemente dibujará una línea perpendicular desde el punto 7 a lo largo del eje y hasta que toque la ecuación lineal y el valor correspondiente en el eje y es la respuesta como se muestra. por la línea punteada verde en el gráfico. Pero vamos a resolver usando la fórmula de una ecuación lineal.

Ahora, si tengo que encontrar el precio de 9,5 kg de manzana, según nuestro modelo mx + b = 5 * 9.5 + 0 = $ 47.5 es la respuesta. A estas alturas, es posible que hayas entendido que metro y B son los ingredientes principales de la ecuación lineal o en otras palabras metro y B son llamados parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.....
Desafortunadamente, este no es el problema del aprendizaje automático ni la ecuación lineal es un algoritmo de predicción, pero afortunadamente la regresión lineal genera el resultado de la misma manera que lo hace la ecuación lineal. El propósito principal del algoritmo de regresión lineal es encontrar el valor de metro y B que se ajustan al modelo y después de eso mismo metro y b se utilizan para predecir el resultado de los datos de entrada dados.
Predecir los precios de la vivienda
Ahora vamos a profundizar un poco más en la solución del problema de regresión. Mire las muestras de datos o también denominada como ejemplos de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... dado en la figura siguiente.
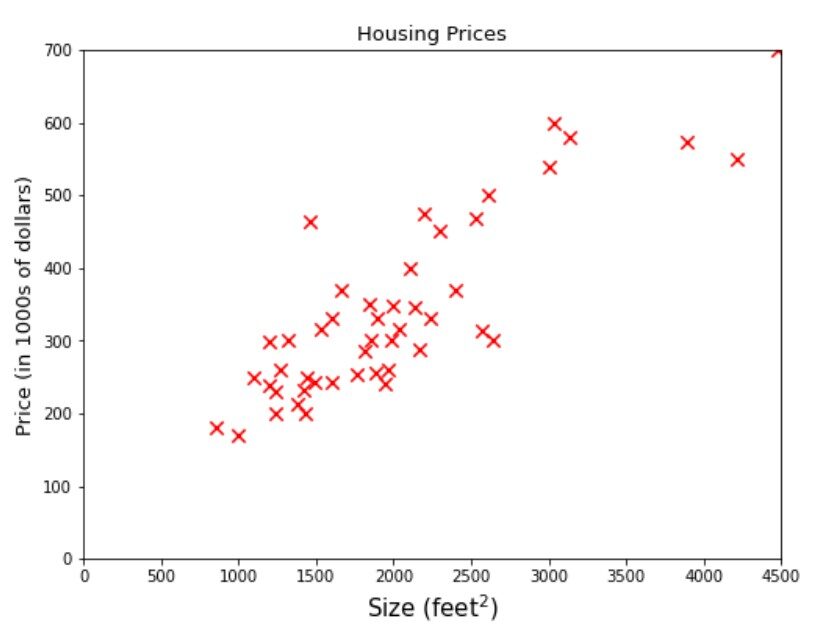
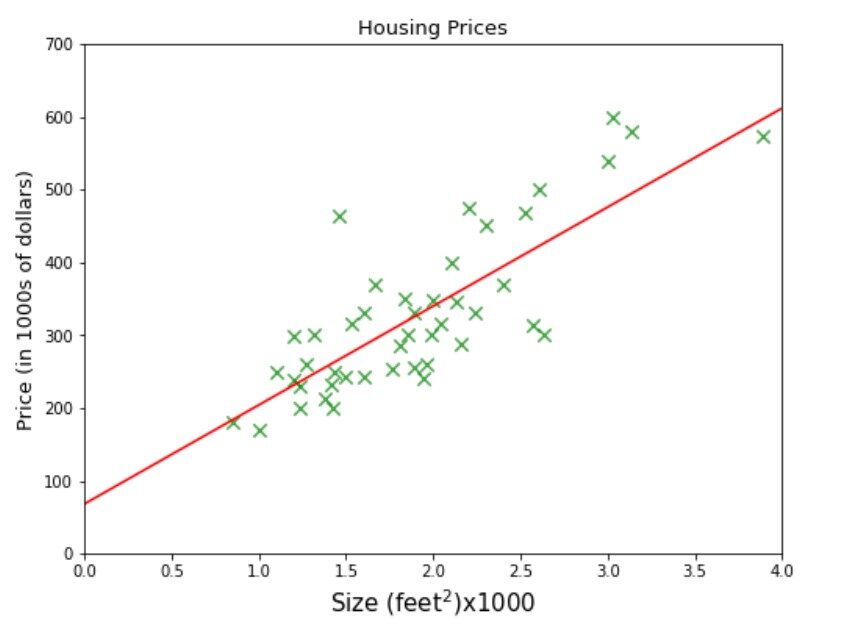
El nombre de una empresa A B C te proporciona un datos sobre el tamaño de las casas y su precio. La empresa requiere proporcionándoles un modelo de aprendizaje automático eso puede predecir los precios de las casas para cualquier dado Talla. Digamos cuál sería el mejor precio estimado para un área de 3000 pies cuadrados. Si estas pensando en ajustar una línea en algún lugar entre el conjunto de datos y dibuje una línea vertical desde 3000 en el eje x hasta que toque la línea y luego el valor correspondiente en el eje y, es decir 470 sería la respuesta, entonces está en el camino correcto, está representado por la línea punteada verde en la figura siguiente.
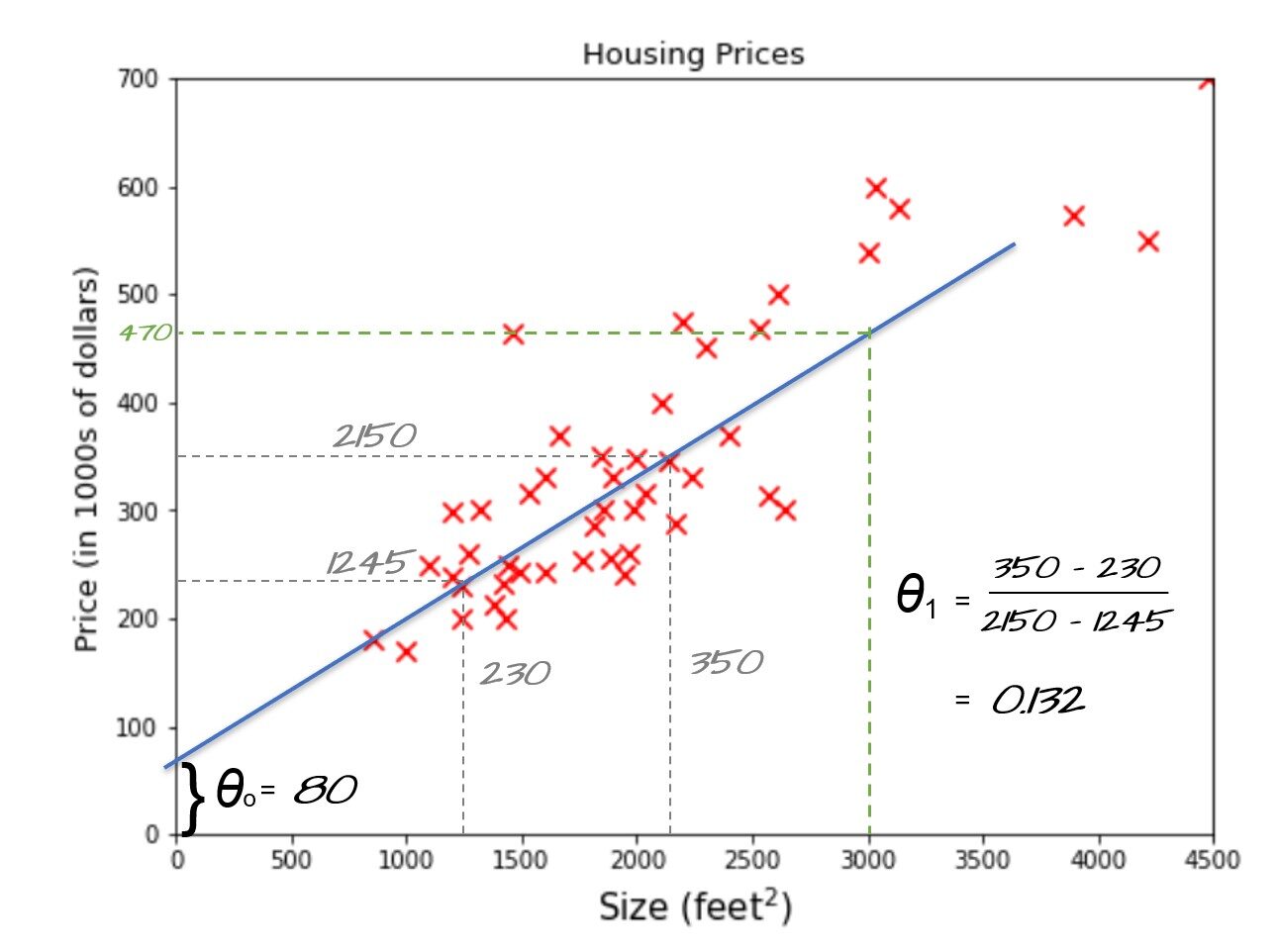
Hagámoslo de otra manera, si pudiéramos encontrar la ecuación de la línea y = mx + b que usamos para ajustar los datos representados por la línea inclinada azul, entonces podemos encontrar fácilmente el modelo que puede predecir los precios de la vivienda para cualquier área dada. . En función de jerga de aprendizaje automático y = mx + b también se llama función de hipótesis dónde myb puede ser representado por theta0 y theta1 respectivamente. theta0 también se llama término de sesgo y theta1, theta2, .. se llaman pesos.
Vea la línea azul en la imagen de arriba. Al tomar dos muestras que se toquen o muy cerca de la línea, podemos encontrar el theta1 (pendiente) = 0.132 y theta cero = 80 como se muestra en la figura. Ahora podemos usar nuestra función de hipótesis para predecir el precio de la vivienda para un tamaño de 3000 pies cuadrados, es decir. 80 + 3000 * 0,132 = 476. $ 476,000 podría ser el mejor precio estimado para una casa de 3000 pies cuadrados y esta podría ser una forma razonable de preparar un modelo de aprendizaje automático cuando acaba de 50 muestras y con solo una característica (tamaño).
Pero el conjunto de datos del mundo real podría ser del orden de miles o incluso millones y la cantidad de características podría variar entre (5–100) o incluso en miles. En ese momento nuestra intuición no será útil para encontrar miles de parámetros con solo mirar un conjunto de datos, por eso necesitamos un algoritmo de aprendizaje automático para realizar un cálculo tan complejo. Tome una taza de café, refrésquese y vuelva de nuevo porque a partir de ahora comprenderá cómo funciona el algoritmo y se le presentarán muchas terminologías nuevas. ¡¡Prepararse!!
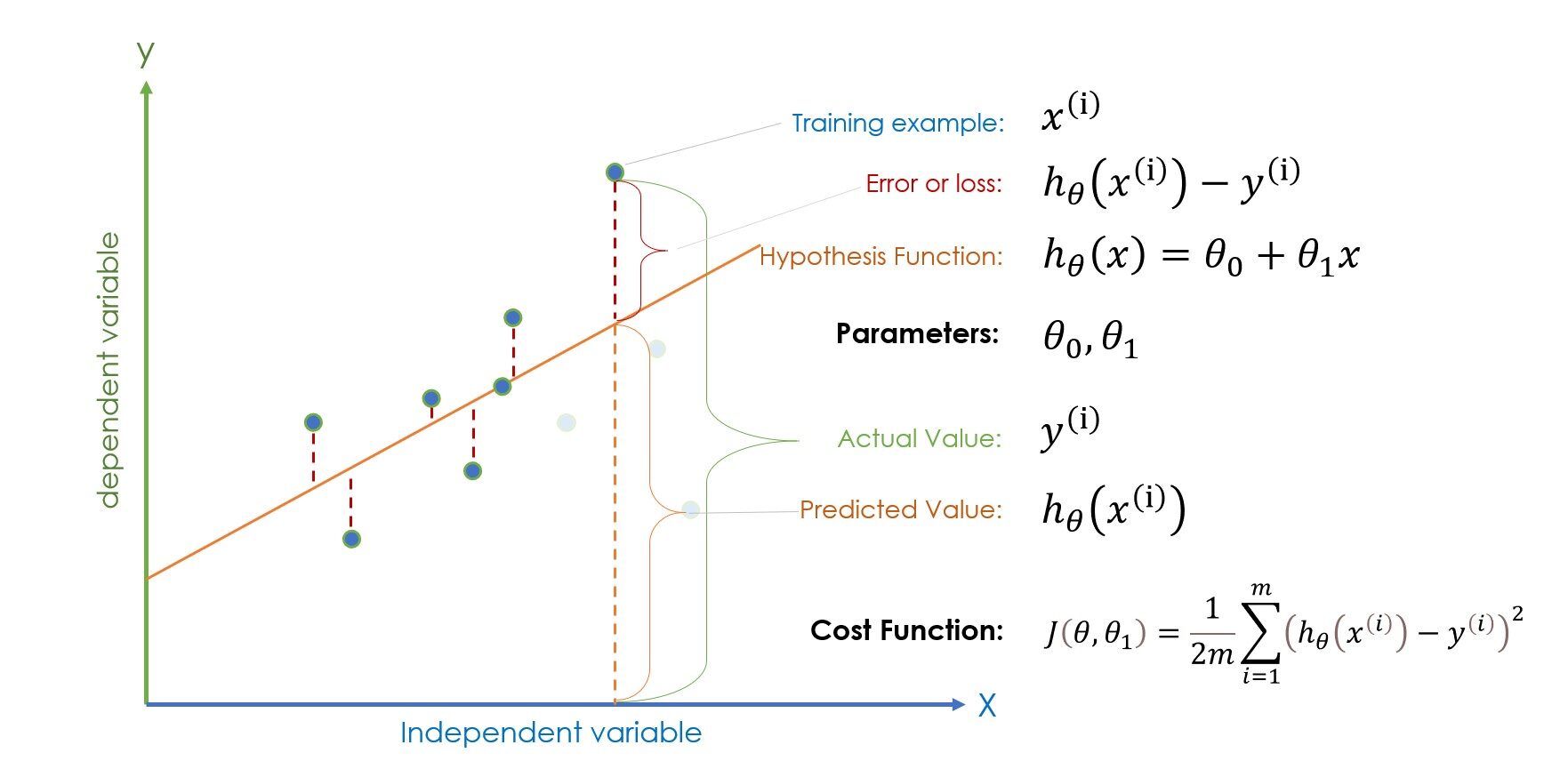
Nota: (i) en la ecuación representa el i-ésimo ejemplo de entrenamiento, no la potencia.
Si las terminologías dadas en la figura anterior le parecen extraterrestres, tómese unos minutos para familiarizarse e intente encontrar una conexión con cada término. Si lo sabe hasta cierto punto, sigamos adelante. Una vez que los valores de los parámetros, es decir término de sesgo y theta1 se inicializan aleatoriamente, la función de hipótesis está lista para la predicción, y luego la error (|valor predicho – valor actual|) se calcula para comprobar si el parámetro inicializado aleatoriamente está dando la predicción correcta o no.
Si el error es demasiado alto, entonces el algoritmo actualiza los parámetros con un nuevo valor, si el error es alto nuevamente, actualizará los parámetros con el nuevo valor nuevamente. El algoritmo continúa este proceso hasta que se minimiza el error. Para minimizar el error tenemos una función especial llamada Descenso de gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en... pero antes de eso, vamos a entender qué Función de costo es y como funciona?

Aquí, en la función de costo, estamos tratando de encontrar el cuadrado de la diferencias entre el valor predicho y el valor real de cada ejemplo de entrenamiento y luego sumar todos los diferencias juntos o en otras palabras, estamos encontrando el cuadrado de error de cada uno ejemplo de entrenamiento y luego resumir todos los errores juntos. La salida que obtenemos es simplemente la media error al cuadrado de un conjunto particular de parámetros. Ok, no más palabras, hagamos el cálculo. Para simplificar el cálculo, usaremos solo un parámetro theta1 y un conjunto de datos muy simple.
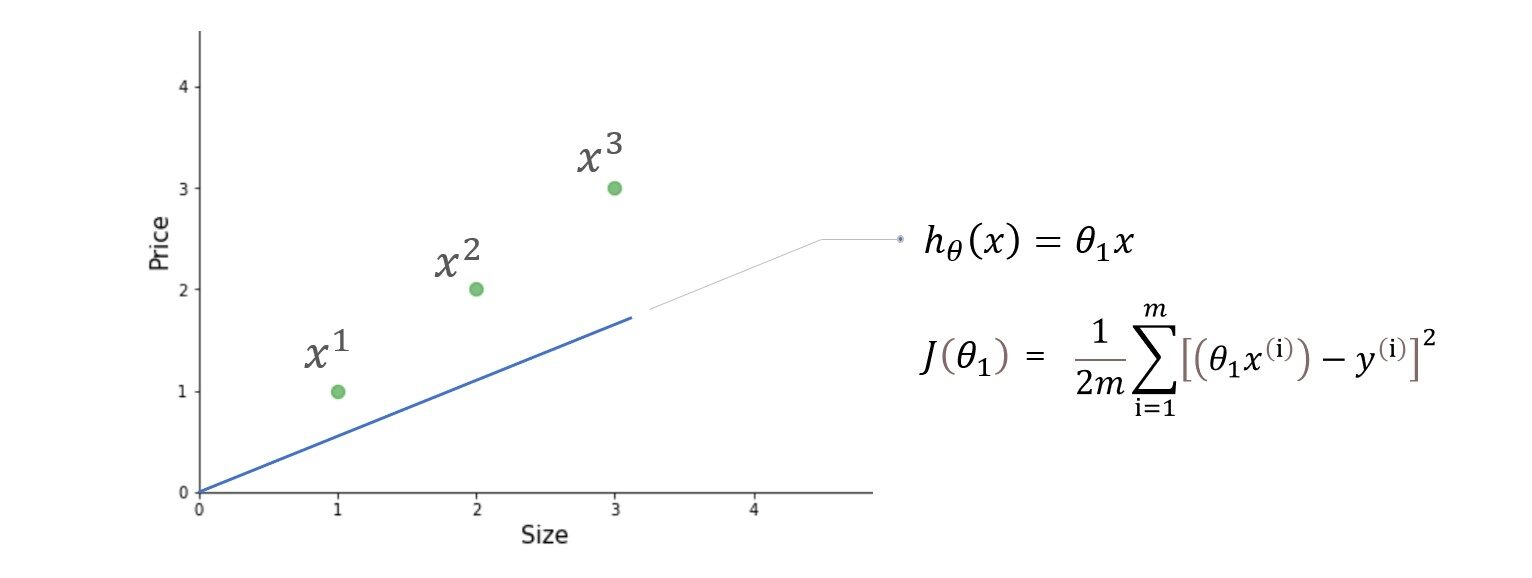
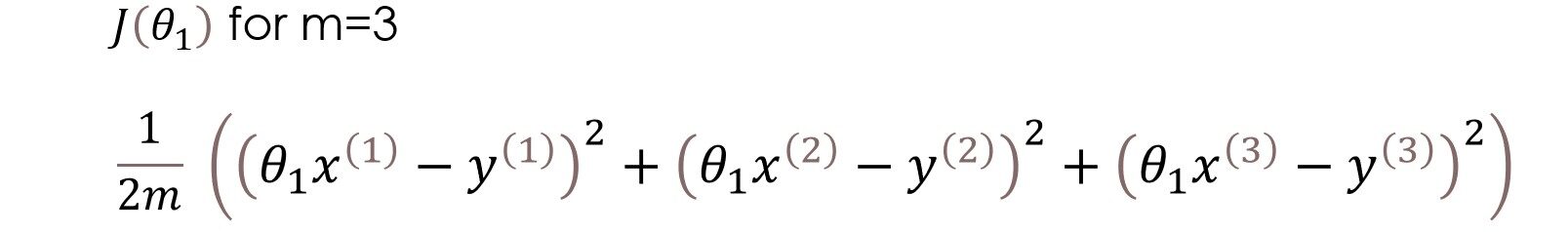
Tenemos tres ejemplos de entrenamiento (X1 = 1, y1 = 1), (X2 = 2, y2 = 2) y (X3 = 3, y3 = 3). la figura de la izquierda es la función de hipótesis y la de la derecha es la función de costo graficada para diferentes valores del parámetro.
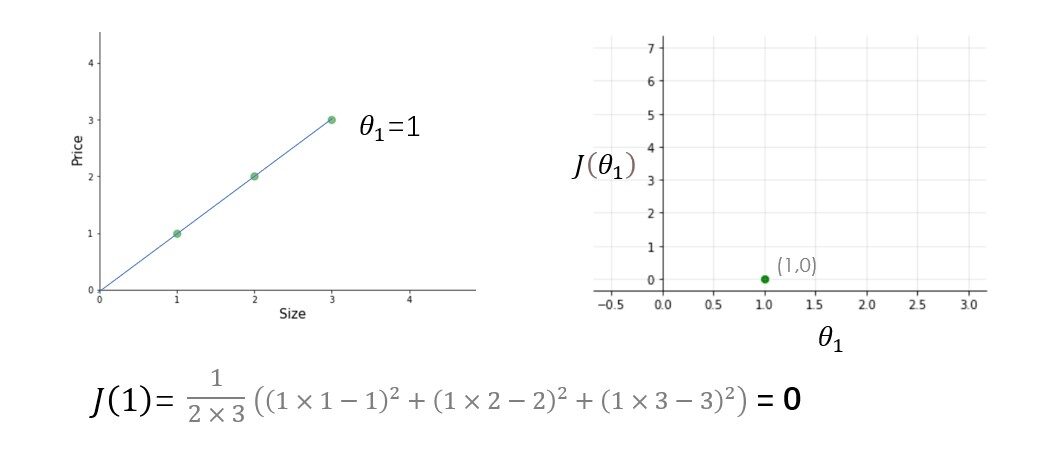
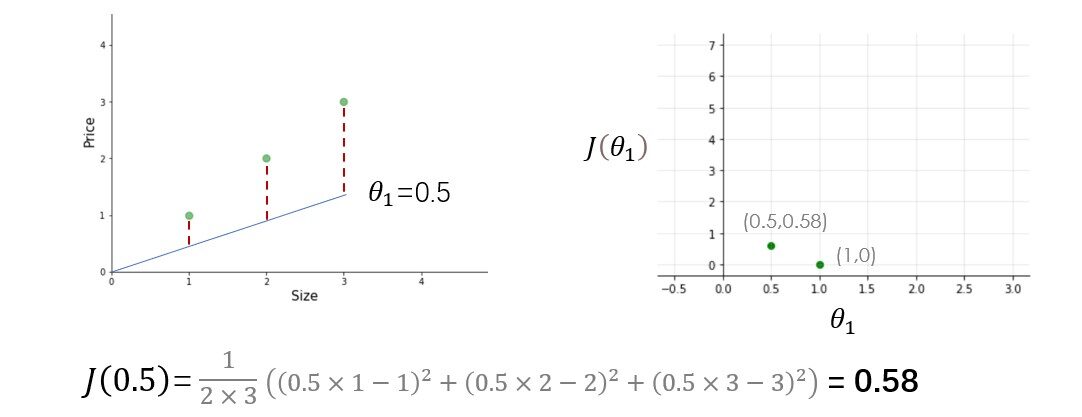
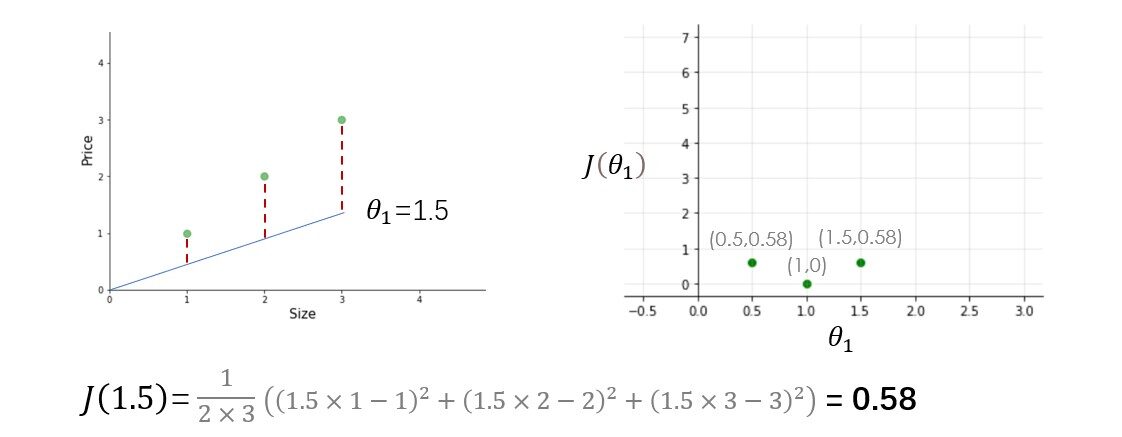
Pruebe otros valores de theta1 usted mismo y calcule el costo de cada valor de theta1. Una vez que trace todos estos puntos, la función de costo se verá como una curva en forma de cuenco como se muestra en la figura siguiente.
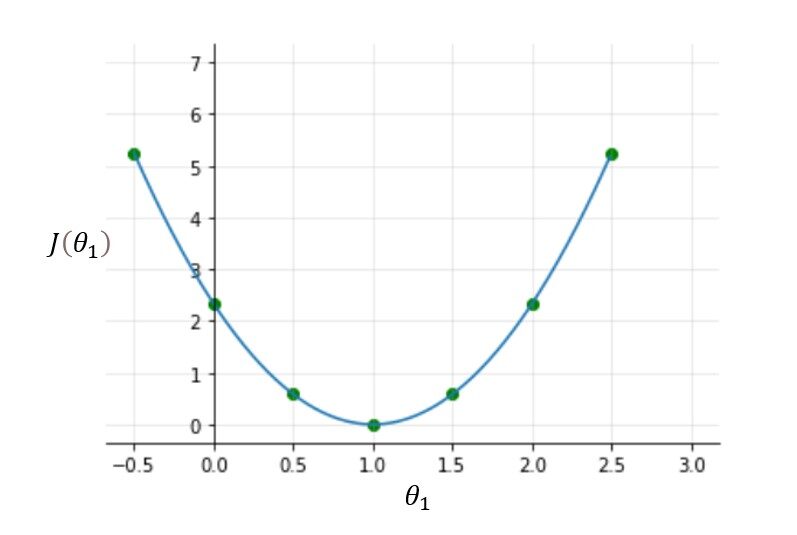
A partir de la figura y el cálculo, está claro que la función de costo es mínima en theta1 = 1 o en la parte inferior de la curva en forma de cuenco. El propósito de todo este arduo trabajo no es calcular el valor mínimo de la función de costo, tenemos una mejor manera de hacer esto, en su lugar, tratamos de comprender el relación Entre parámetros, función de hipótesis, y función de costo. Asegúrese de comprender todos estos conceptos antes de seguir adelante.
Función de coste de codificación:

Descenso de gradiente:
¿Por qué necesitamos un descenso en gradiente?
- En breve para minimizar la función de costo, ¿Pero cómo? Vamos a ver
La función de costo solo funciona cuando conoce los valores de los parámetros.En el ejemplo de muestra anterior, elegimos manualmente el valor de los parámetros cada vez, pero durante el cálculo algorítmico, una vez que los valores de los parámetros se inicializan aleatoriamente, es el descenso del gradiente quien tiene que decidir qué parámetros. valor a elegir en la siguiente iteración para minimizar el error, es el descenso del gradiente quien decide cuánto aumentar o disminuir los valores de los parámetros.
Analogía: ¿Cómo funciona Gradient Descent?
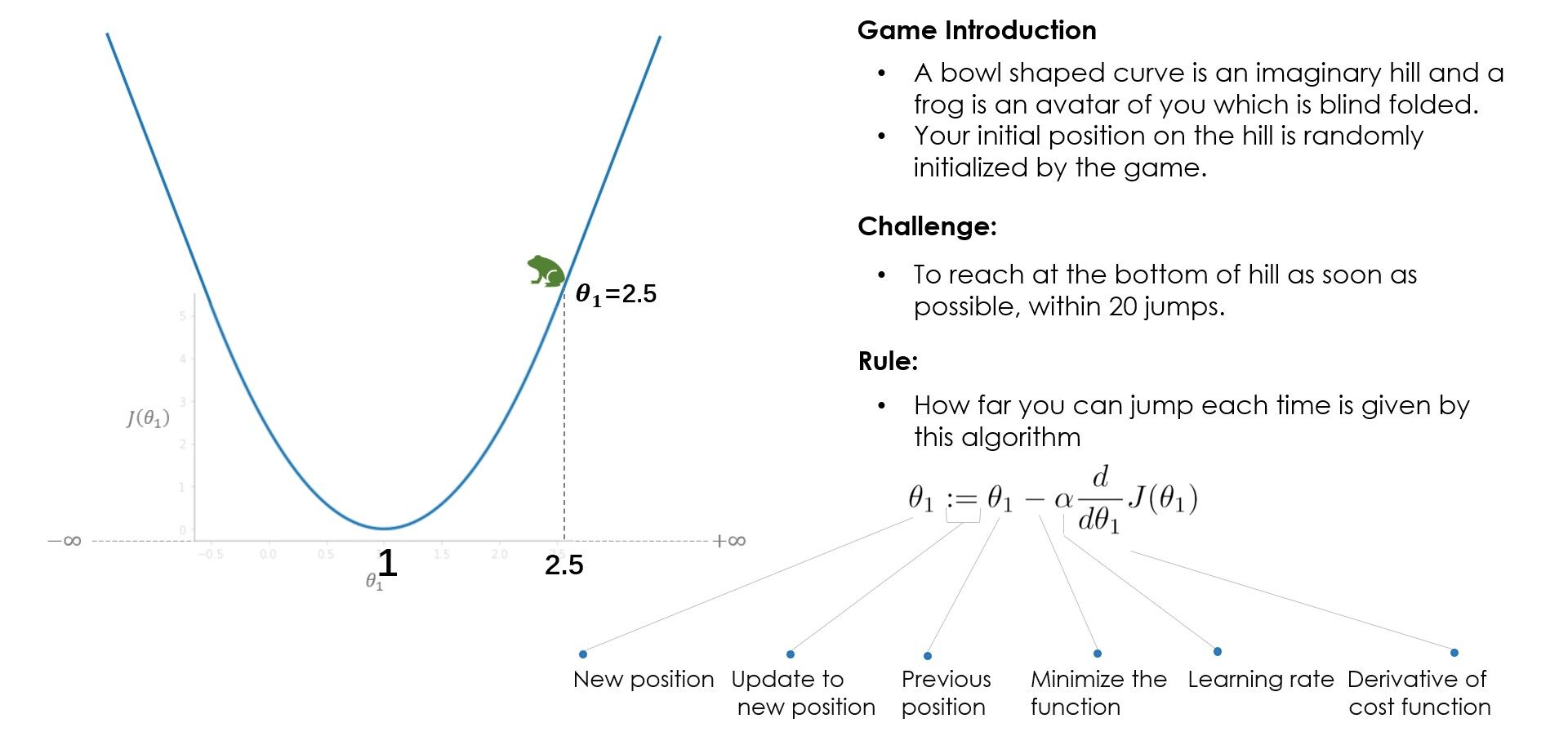
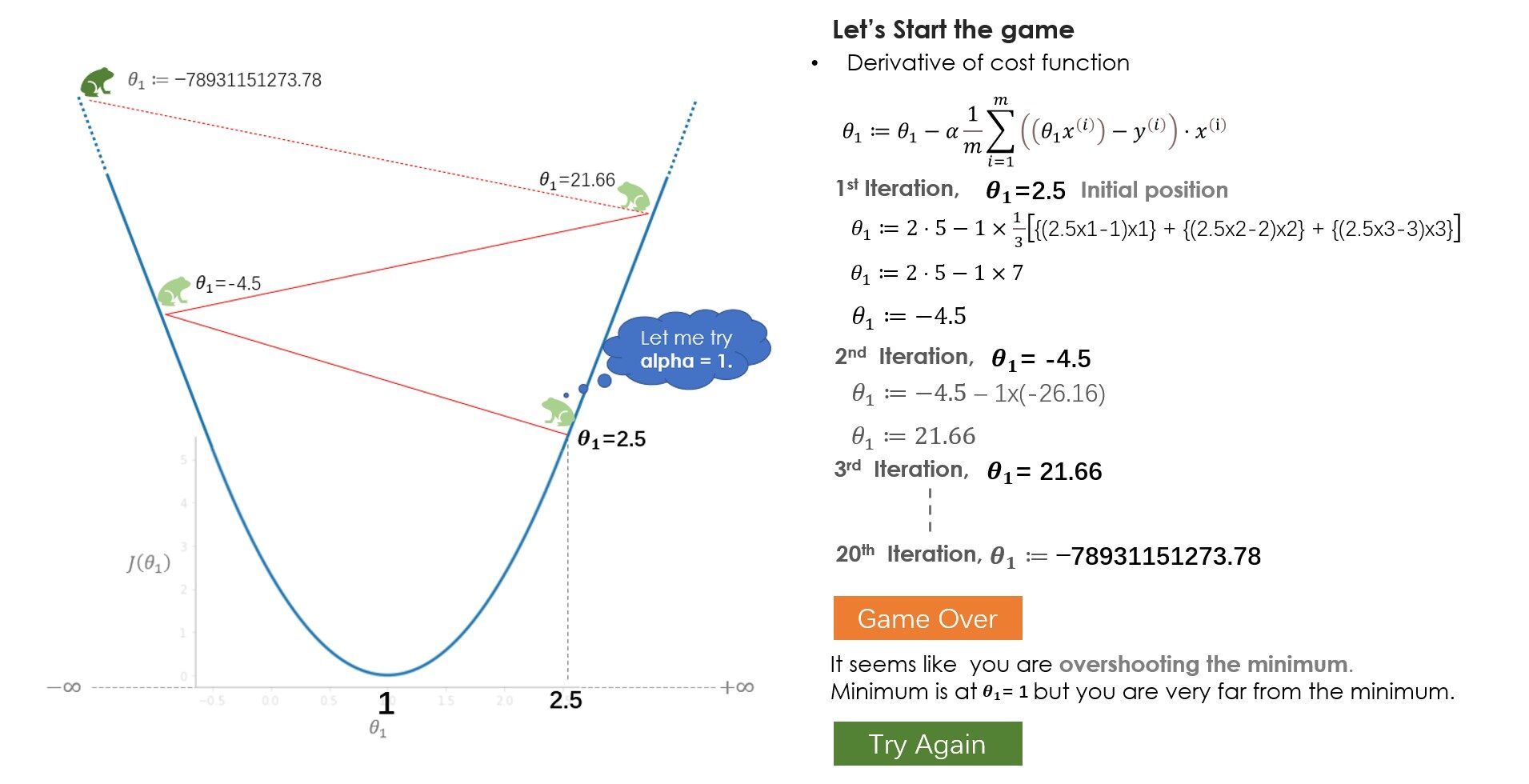
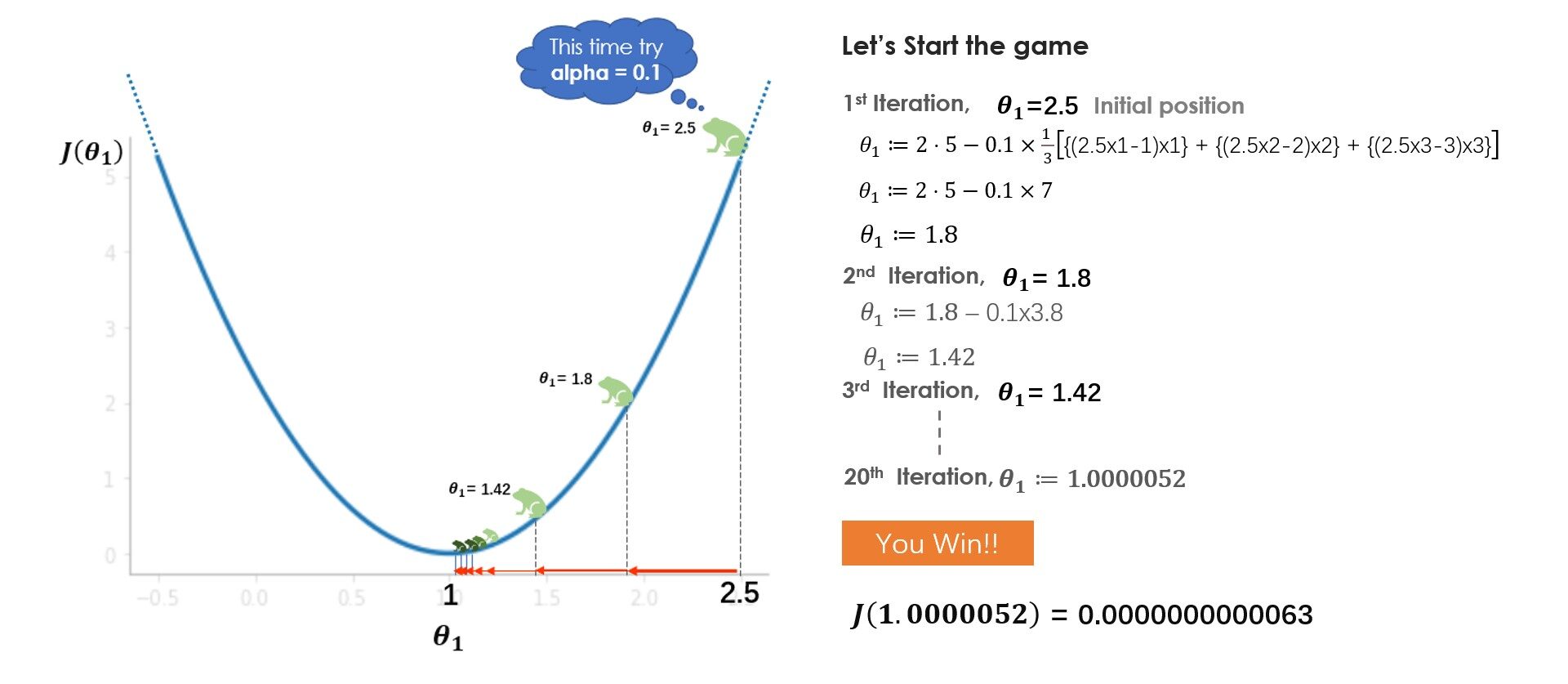
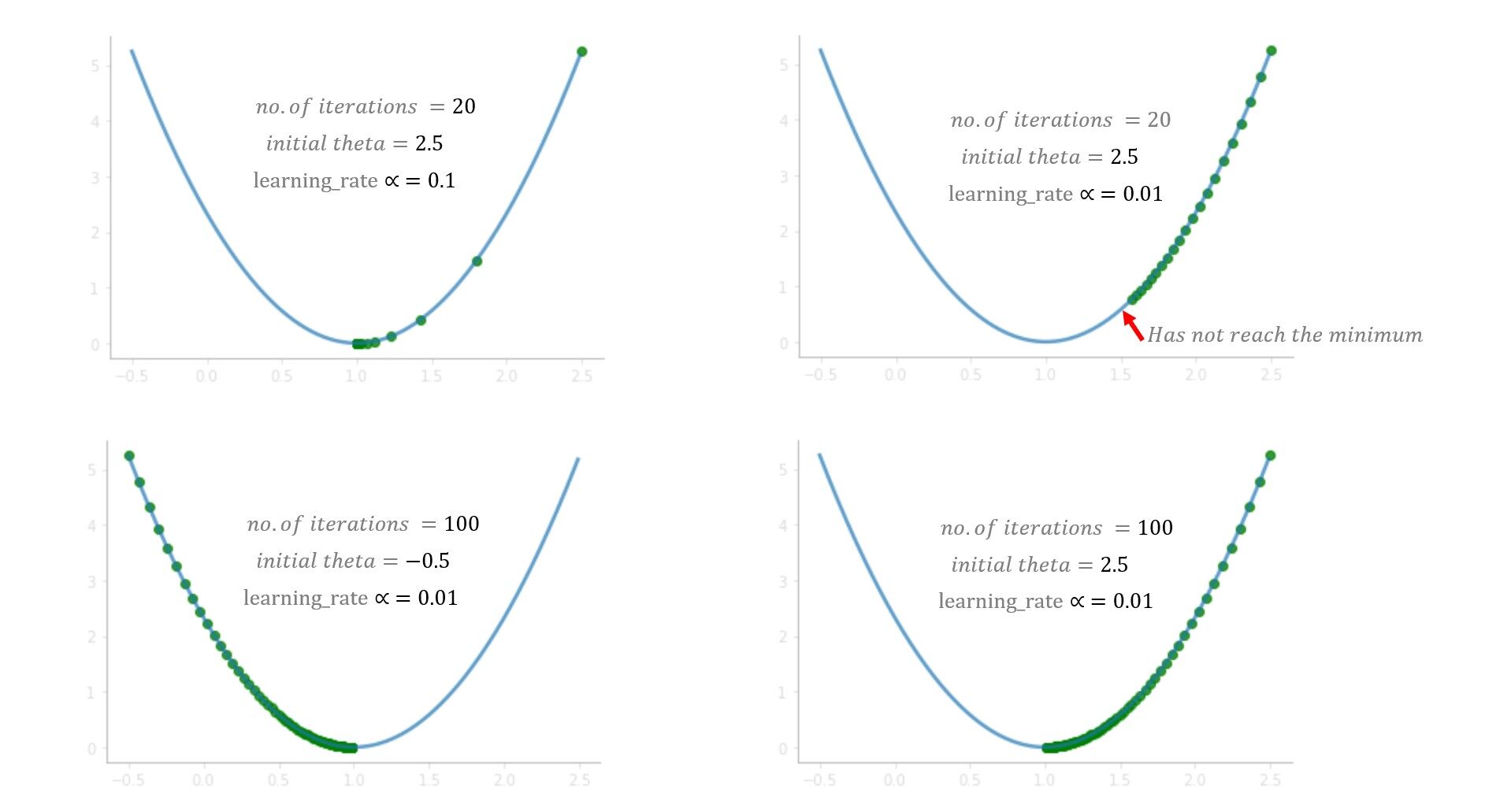
¿Qué aprendiste del juego? Al principio, intentas con una tasa de aprendizaje (alfa) = 1 pero no alcanzas el mínimo, debido a que los pasos más grandes sobrepasan el mínimo. En el siguiente juego, intentas con alpha = 0.1, y esta vez lograste llegar al fondo de manera muy segura. ¿Qué pasaría si hubieras intentado con alfa = 0.01? Bueno, en ese caso, irás bajando gradualmente pero no llegarás al fondo, 20 saltos no son suficientes para llegar al fondo con alfa = 0.01, 100 saltos podrían ser suficiente. Mientras se resuelve un problema del mundo real, normalmente un alfa entre 0.01–0.1 debería funcionar bien, pero varía con el número de iteraciones que toma el algoritmo, algunos problemas pueden requerir 100 o incluso 1000 iteraciones.
En función de estos factores, puede probar con diferentes valores de alfa. Aunque ajustar el valor alfa es una de las tareas importantes para comprender el algoritmo, le sugiero que mire otras partes del algoritmo también como las partes derivadas, el signo menos, los parámetros de actualización y comprenda cuáles son los roles de sus individuos.
Descenso de gradiente de codificación

Hasta ahora, solo estamos usando un único parámetro para calcular la función de costo y los algoritmos. ¿Cómo se ve la función de costo y cómo funciona el algoritmo cuando tenemos dos o más parámetros? Consulte la figura siguiente para obtener una comprensión intuitiva. Imagínese en algún lugar de la cima de la montaña y luchando por bajar la base de la montaña con los ojos vendados.
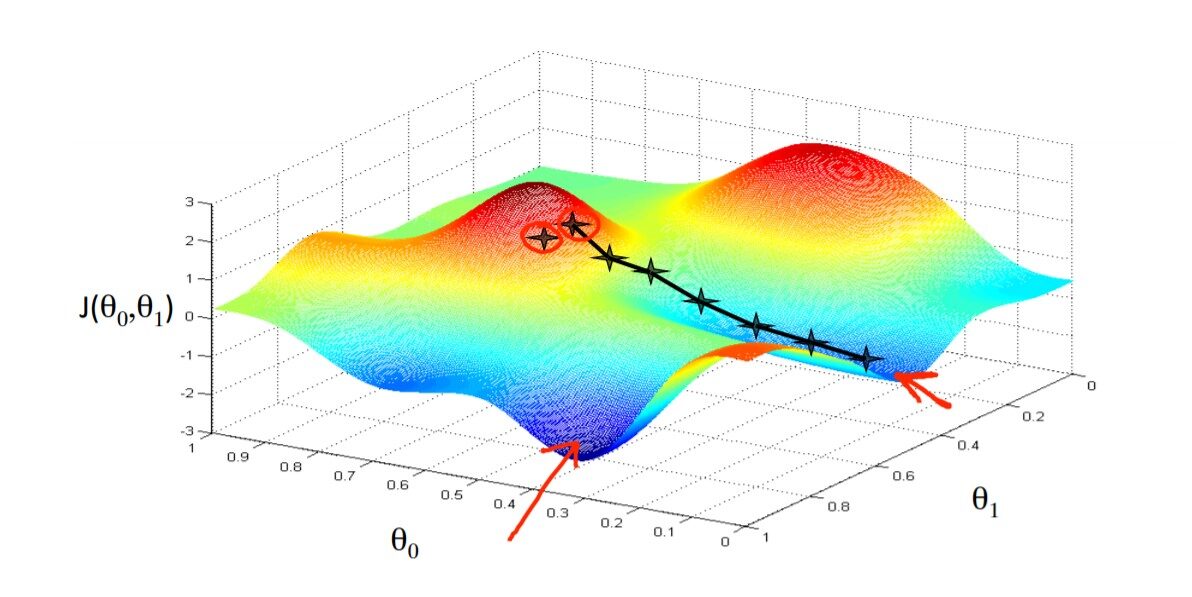
El principio de funcionamiento del algoritmo es el mismo para cualquier número de parámetros, es solo que cuanto más los parámetros más la dirección de la pendiente. En el ejemplo anterior de la curva en forma de cuenco, solo necesitamos observar la pendiente de theta1, pero ahora el algoritmo debe buscar en ambas direcciones para minimizar la función de costo. codifiquemos y entendamos el algoritmo. consulte la figura siguiente como referencia:



Aquí vamos, nuestro modelo predice 475,88 * 1000 = $ 475,880 para la casa de tamaño 3 * 1000 pies cuadrados. Está muy cerca de nuestra predicción que hicimos al principio usando nuestra intuición.
Conclusión
Como principiante, puede ser un poco difícil comprender todos los conceptos de regresión lineal en tan poco tiempo de lectura. No diría que sabe todo sobre la regresión lineal de este artículo. El propósito de este artículo es hacer que los algoritmos sean comprensibles de la manera más simple posible. Siga el enlace de recursos a continuación para una mejor comprensión. Espero que hayas disfrutado leyendo el artículo. Gracias por leer.
Recursos:
enlace de código
https://github.com/ravi235/LinearRegression
Matemáticas de descenso de gradiente
https://www.youtube.com/watch?v=jc2IthslyzM&ab_channel=TheCodingTrain
Regresión lineal Andrew Ng
https://www.youtube.com/watch?v=kHwlB_j7Hkc&t=8s&ab_channel=ArtificialIntelligence-AllinOne






