Comencemos tomando un pequeño enunciado del problema.
Enunciado del problema: cree un modelo de regresión lineal simple para predecir el aumento salarial utilizando años de experiencia.
Comience importando las bibliotecas necesarias
las bibliotecas necesarias son pandas, NumPy para trabajar con marcos de datos, matplotlib, seaborn para visualizaciones y sklearn, statsmodels para construir modelos de regresión.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from scipy import stats
from scipy.stats import probplot
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn import preprocessing
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_scoreUna vez que terminamos con la importación de bibliotecas, creamos un marco de datos de pandas a partir del archivo CSV
df = pd.read_csv(“Salary_Data.csv”)
Realizar EDA (análisis de datos exploratorios)
Los pasos básicos de EDA son:
- Identificar la cantidad de características o columnas
- Identificar las características o columnas
- Identificar el tamaño del conjunto de datos
- Identificación de los tipos de datos de las características
- Verificando si el conjunto de datos tiene celdas vacías
- Identificar la cantidad de celdas vacías por características o columnas
- Manejo de valores perdidos y valores atípicos
- Codificación de variables categóricas
- Análisis gráfico univariado, bivariado
- NormalizaciónLa normalización es un proceso fundamental en diversas disciplinas, que busca establecer estándares y criterios uniformes para mejorar la calidad y la eficiencia. En contextos como la ingeniería, la educación y la administración, la normalización facilita la comparación, la interoperabilidad y la comprensión mutua. Al implementar normas, se promueve la cohesión y se optimizan recursos, lo que contribuye al desarrollo sostenible y a la mejora continua de los procesos.... y escalado
len(df.columns) # identify the number of featuresdf.columns # idenfity the features
df.shape # identify the size of of the datasetUn "dataset" o conjunto de datos es una colección estructurada de información, que puede ser utilizada para análisis estadísticos, machine learning o investigación. Los datasets pueden incluir variables numéricas, categóricas o textuales, y su calidad es crucial para obtener resultados fiables. Su uso se extiende a diversas disciplinas, como la medicina, la economía y la ciencia social, facilitando la toma de decisiones informadas y el desarrollo de modelos predictivos....df.dtypes # identify the datatypes of the featuresdf.isnull().values.any() # checking if dataset has empty cellsdf.isnull().sum() # identify the number of empty cellsNuestro conjunto de datos tiene dos columnas: Años de experiencia, Salario. Y ambos son de tipo de datos flotante. Tenemos 30 registros y no tenemos valores nulos ni valores atípicos en nuestro conjunto de datos.
Análisis gráfico univariado
Para el análisis univariado, tenemos Histograma, gráfico de densidad, diagrama de caja o violín, y Gráfico QQ normal. Nos ayudan a comprender la distribución de los puntos de datos y la presencia de valores atípicos.
Un diagrama de violínEl diagrama de violín es una representación gráfica que combina características de un boxplot y un gráfico de densidad. Se utiliza para visualizar la distribución de un conjunto de datos, mostrando tanto la mediana como la variabilidad a través de su forma, que se asemeja a un violín. Este tipo de gráfico es muy útil en análisis estadísticos, ya que permite comparar múltiples distribuciones de forma clara y efectiva.... es un método para trazar datos numéricos. Es similar a un diagrama de caja, con la adición de un diagrama de densidad de grano rotado en cada lado.
Código Python:
# Histogram
# We can use either plt.hist or sns.histplot
plt.figure(figsize=(20,10))
plt.subplot(2,4,1)
plt.hist(df['YearsExperience'], density=False)
plt.title("Histogram of 'YearsExperience'")
plt.subplot(2,4,5)
plt.hist(df['Salary'], density=False)
plt.title("Histogram of 'Salary'")
# Density plot
plt.subplot(2,4,2)
sns.distplot(df['YearsExperience'], kde=True)
plt.title("Density distribution of 'YearsExperience'")
plt.subplot(2,4,6)
sns.distplot(df['Salary'], kde=True)
plt.title("Density distribution of 'Salary'")
# boxplot or violin plot
# A violin plot is a method of plotting numeric data. It is similar to a box plot,
# with the addition of a rotated kernel density plot on each side
plt.subplot(2,4,3)
# plt.boxplot(df['YearsExperience'])
sns.violinplot(df['YearsExperience'])
# plt.title("Boxlpot of 'YearsExperience'")
plt.title("Violin plot of 'YearsExperience'")
plt.subplot(2,4,7)
# plt.boxplot(df['Salary'])
sns.violinplot(df['Salary'])
# plt.title("Boxlpot of 'Salary'")
plt.title("Violin plot of 'Salary'")
# Normal Q-Q plot
plt.subplot(2,4,4)
probplot(df['YearsExperience'], plot=plt)
plt.title("Q-Q plot of 'YearsExperience'")
plt.subplot(2,4,8)
probplot(df['Salary'], plot=plt)
plt.title("Q-Q plot of 'Salary'")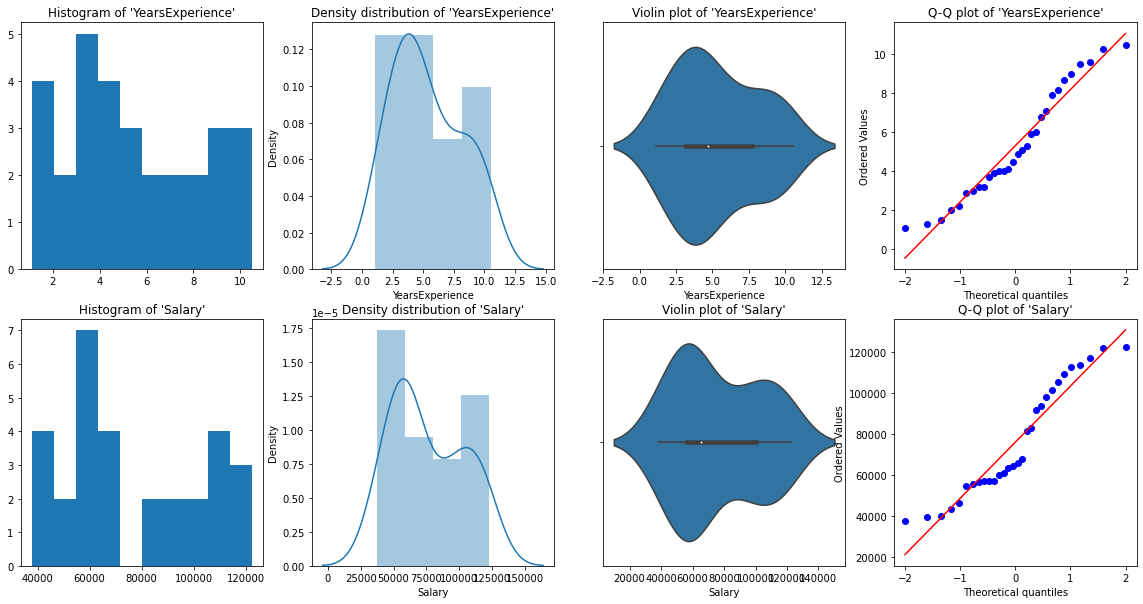
De las representaciones gráficas anteriores, podemos decir que no hay valores atípicos en nuestros datos, y YearsExperience looks like normally distributed, and Salary doesn't look normal. Podemos verificar esto usando Shapiro Test.
Código Python:
# Def a function to run Shapiro test
# Defining our Null, Alternate Hypothesis
Ho = 'Data is Normal'
Ha="Data is not Normal"
# Defining a significance value
alpha = 0.05
def normality_check(df):
for columnName, columnData in df.iteritems():
print("Shapiro test for {columnName}".format(columnName=columnName))
res = stats.shapiro(columnData)
# print(res)
pValue = round(res[1], 2)
# Writing condition
if pValue > alpha:
print("pvalue = {pValue} > {alpha}. We fail to reject Null Hypothesis. {Ho}".format(pValue=pValue, alpha=alpha, Ho=Ho))
else:
print("pvalue = {pValue} <= {alpha}. We reject Null Hypothesis. {Ha}".format(pValue=pValue, alpha=alpha, Ha=Ha))
# Drive code
normality_check(df)Nuestro instinto de los gráficos fue correcto. Años La experiencia se distribuye normalmente y el salario no se distribuye normalmente.
Visualización bivariada
para datos numéricos frente a datos numéricos, podemos trazar los siguientes gráficos
- Gráfico de dispersión
- Gráfico de línea
- Mapa de calor para correlación
- Parcela conjunta
Código Python para varias parcelas:
# Scatterplot & Line plots
plt.figure(figsize=(20,10))
plt.subplot(1,3,1)
sns.scatterplot(data=df, x="YearsExperience", y="Salary", hue="YearsExperience", alpha=0.6)
plt.title("Scatter plot")
plt.subplot(1,3,2)
sns.lineplot(data=df, x="YearsExperience", y="Salary")
plt.title("Line plot of YearsExperience, Salary")
plt.subplot(1,3,3)
sns.lineplot(data=df)
plt.title('Line Plot')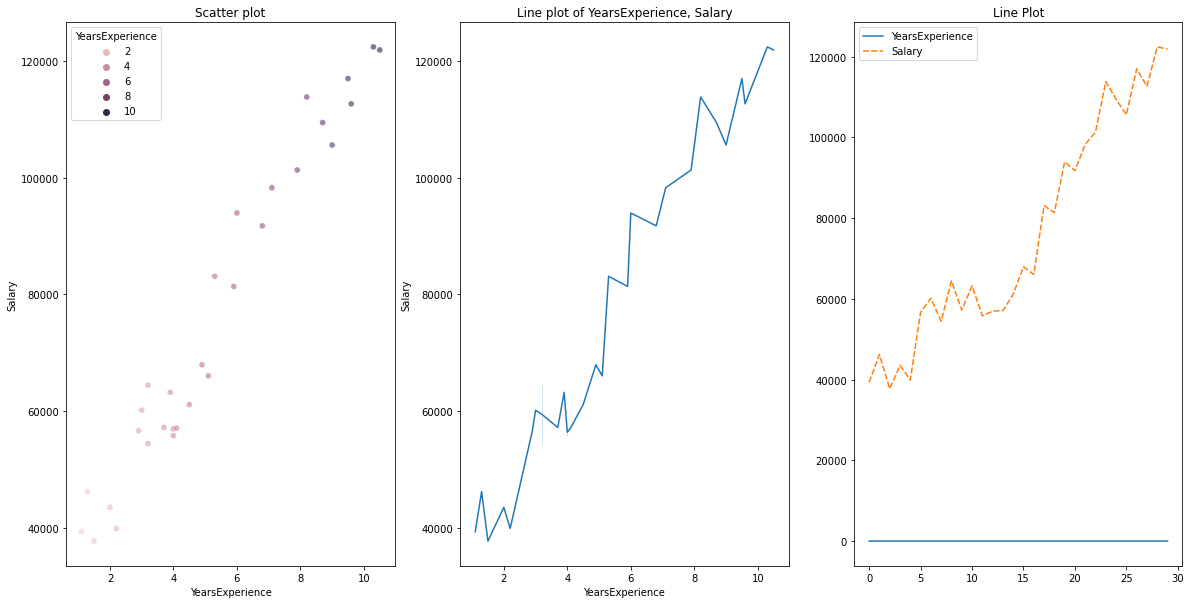
# heatmap
plt.figure(figsize=(10, 10))
plt.subplot(1, 2, 1)
sns.heatmap(data=df, cmap="YlGnBu", annot = True)
plt.title("Heatmap using seaborn")
plt.subplot(1, 2, 2)
plt.imshow(df, cmap ="YlGnBu")
plt.title("Heatmap using matplotlib")
# Joint plot
sns.jointplot(x = "YearsExperience", y = "Salary", kind = "reg", data = df)
plt.title("Joint plot using sns")
# kind can be hex, kde, scatter, reg, hist. When kind='reg' it shows the best fit line.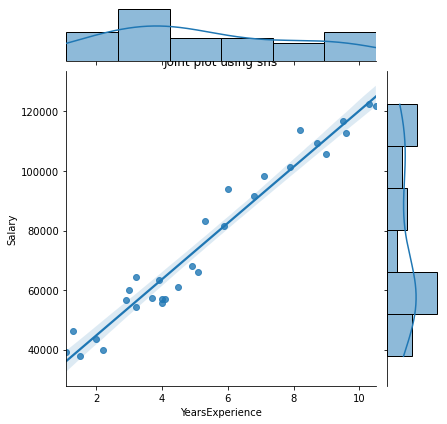
Verifique si existe alguna correlación entre las variables usando df.corr ()
print("Correlation: "+ 'n', df.corr()) # 0.978 which is high positive correlation
# Draw a heatmap for correlation matrix
plt.subplot(1,1,1)
sns.heatmap(df.corr(), annot=True)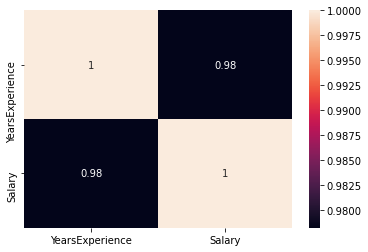
correlación = 0,98, que es una alta correlación positiva. Esto significa que la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente aumenta a medida que aumenta la variable independiente.
Normalización
Como podemos ver, hay una gran diferencia entre los valores de las columnas YearsExperience, Salario. Nosotros podemos usar Normalization para cambiar los valores de las columnas numéricas en el conjunto de datos para usar una escala común, sin distorsionar las diferencias en los rangos de valores ni perder información.
Usamos sklearn.preprocessing.Normalize para normalizar nuestros datos. Devuelve valores entre 0 y 1.
# Create new columns for the normalized values
df['Norm_YearsExp'] = preprocessing.normalize(df[['YearsExperience']], axis=0)
df['Norm_Salary'] = preprocessing.normalize(df[['Salary']], axis=0)
df.head()Regresión lineal usando scikit-learn
LinearRegression(): LinearRegression se ajusta a un modelo lineal con coeficientes β = (β1,…, βp) para minimizar la suma residual de cuadrados entre los objetivos observados en el conjunto de datos y los objetivos predichos por la aproximación lineal.
def regression(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# print(x,y)
# Instantiating the LinearRegression object
regressor = LinearRegression()
# Training the model
regressor.fit(x,y)
# Checking the coefficients for the prediction of each of the predictor
print('n'+"Coeff of the predictor: ",regressor.coef_)
# Checking the intercept
print("Intercept: ",regressor.intercept_)
# Predicting the output
y_pred = regressor.predict(x)
# print(y_pred)
# Checking the MSE
print("Mean squared error(MSE): %.2f" % mean_squared_error(y, y_pred))
# Checking the R2 value
print("Coefficient of determination: %.3f" % r2_score(y, y_pred)) # Evaluates the performance of the model # says much percentage of data points are falling on the best fit line
# visualizing the results.
plt.figure(figsize=(18, 10))
# Scatter plot of input and output values
plt.scatter(x, y, color="teal")
# plot of the input and predicted output values
plt.plot(x, regressor.predict(x), color="Red", linewidth=2 )
plt.title('Simple Linear Regression')
plt.xlabel('YearExperience')
plt.ylabel('Salary')
# Driver code
regression(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
regression(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracyLogramos una precisión del 95,7% con scikit-learn, pero no hay mucho margenEl margen es un término utilizado en diversos contextos, como la contabilidad, la economía y la impresión. En contabilidad, se refiere a la diferencia entre los ingresos y los costos, lo que permite evaluar la rentabilidad de un negocio. En el ámbito editorial, el margen es el espacio en blanco alrededor del texto en una página, que facilita la lectura y proporciona una presentación estética. Su correcta gestión es esencial... para comprender la información detallada sobre la relevancia de las características de este modelo. Así que construyamos un modelo usando statsmodels.api, statsmodels.formula.api
Regresión lineal usando statsmodel.formula.api (smf)
Los predictores en statsmodels.formula.api deben enumerarse individualmente. Y en este método, se agrega automáticamente una constante a los datos.
def smf_ols(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# print(x)
# train the model
model = smf.ols('y~x', data=df).fit()
# print model summary
print(model.summary())
# Predict y
y_pred = model.predict(x)
# print(type(y), type(y_pred))
# print(y, y_pred)
y_lst = y.Salary.values.tolist()
# y_lst = y.iloc[:, -1:].values.tolist()
y_pred_lst = y_pred.tolist()
# print(y_lst)
data = [y_lst, y_pred_lst]
# print(data)
res = pd.DataFrame({'Actuals':data[0], 'Predicted':data[1]})
# print(res)
plt.scatter(x=res['Actuals'], y=res['Predicted'])
plt.ylabel('Predicted')
plt.xlabel('Actuals')
res.plot(kind='bar',figsize=(10,6))
# Driver code
smf_ols(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
# smf_ols(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracy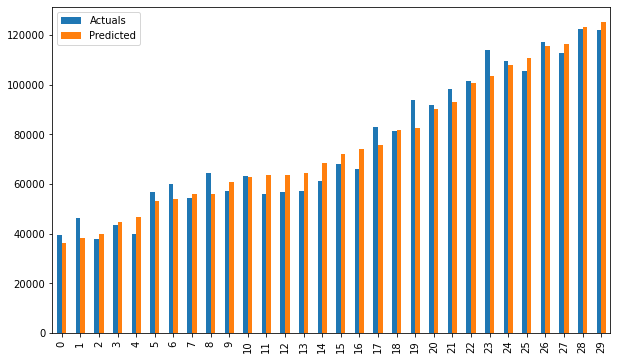
Regresión usando statsmodels.api
Ya no es necesario enumerar los predictores individualmente.
statsmodels.regression.linear_model.OLS (endog, exog)
endoges la variable dependienteexoges la variable independiente. Una intercepción no está incluida de forma predeterminada y debe ser agregada por el usuario (usando add_constant).
# Create a helper function
def OLS_model(df):
# defining the independent and dependent features
x = df.iloc[:, 1:2]
y = df.iloc[:, 0:1]
# Add a constant term to the predictor
x = sm.add_constant(x)
# print(x)
model = sm.OLS(y, x)
# Train the model
results = model.fit()
# print('n'+"Confidence interval:"+'n', results.conf_int(alpha=0.05, cols=None)) #Returns the confidence interval of the fitted parameters. The default alpha=0.05 returns a 95% confidence interval.
print('n'"Model parameters:"+'n',results.params)
# print the overall summary of the model result
print(results.summary())
# Driver code
OLS_model(df[['Salary', 'YearsExperience']]) # 0.957 accuracy
OLS_model(df[['Norm_Salary', 'Norm_YearsExp']]) # 0.957 accuracyLogramos una precisión del 95,7%, lo cual es bastante bueno 🙂
¿Qué dice la tabla de resumenLa "tabla de resumen" es una herramienta eficaz que condensa información clave de un tema específico en un formato visual y accesible. Utilizada en diversos campos, como la educación y la investigación, facilita la comprensión y el análisis de datos. Su estructura permite a los usuarios identificar rápidamente los puntos esenciales, promoviendo una mejor retención del conocimiento y una comparación más sencilla entre diferentes conceptos o variables.... del modelo? 😕
Siempre es importante comprender ciertos términos de la tabla de resumen del modelo de regresión para que podamos conocer el rendimiento de nuestro modelo y la relevancia de las variables de entrada.
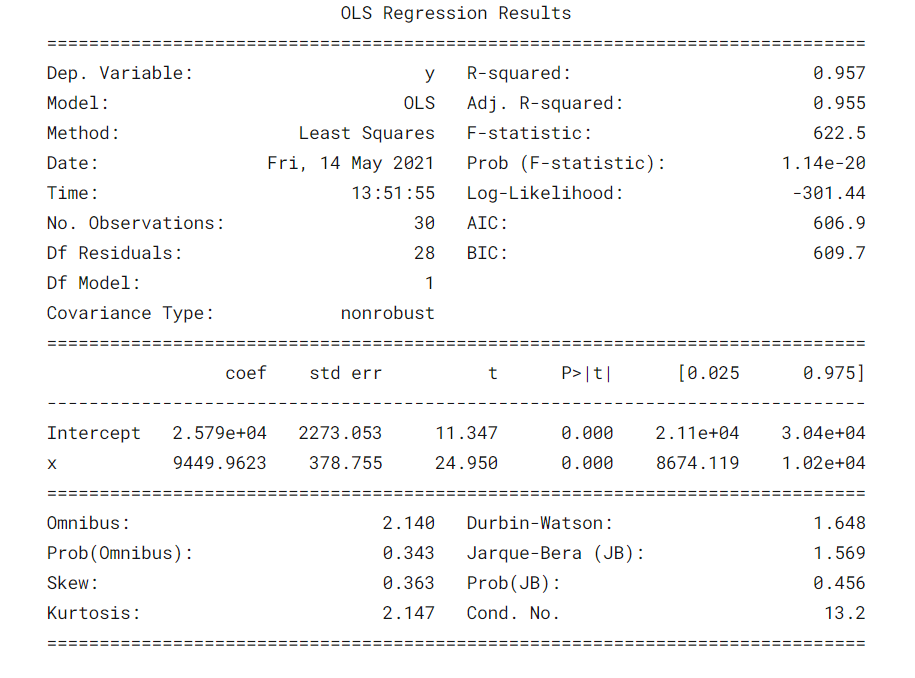
Algunos parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.... importantes que deben tenerse en cuenta son el valor de R cuadrado, Adj. Valor R cuadrado, estadístico F, prob (estadístico F), coeficiente de intercepto y variables de entrada, p> | t |.
- R-Cuadrado es el coeficiente de determinación. Una medida estadística que dice que gran parte de los puntos de datos se encuentran en la línea de mejor ajuste. Se espera un valor de R cuadrado más cercano a 1 para que un modelo se ajuste bien.
- Adj. R-cuadrado penaliza el valor de R-cuadrado si seguimos agregando las nuevas características que no contribuyen a la predicción del modelo. Si Adj. Valor de R cuadrado <valor de R cuadrado, es una señal de que tenemos predictores irrelevantes en el modelo.
- La estadística F o prueba F nos ayuda a aceptar o rechazar la hipótesis nulaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos..... Compara el modelo de solo intercepción con nuestro modelo con características. La hipótesis nula es «todos los coeficientes de regresión son iguales a cero y eso significa que ambos modelos son iguales». La hipótesis alternativa es ‘interceptar el único modelo es peor que nuestro modelo, lo que significa que nuestros coeficientes añadidos mejoraron el rendimiento del modelo. Si prob (estadístico F) <0.05 y el estadístico F es un valor alto, rechazamos la hipótesis nula. Significa que existe una buena relación entre las variables de entrada y salida.
- coef muestra los coeficientes estimados de las características de entrada correspondientes
- T-test habla de la relación entre la salida y cada una de las variables de entrada individualmente. La hipótesis nula es ‘el coeficiente de una característica de entrada es 0’. La hipótesis alternativa es ‘el coeficiente de una característica de entrada no es 0’. Si pvalue 0.05.
Bueno, ahora sabemos cómo sacar inferencias importantes de la tabla de resumen del modelo, así que ahora veamos los parámetros de nuestro modelo y evaluemos nuestro modelo.
En nuestro caso, el valor de R cuadrado (0,957) está cerca de Adj. El valor de R cuadrado (0,955) es una buena señal de que las características de entrada están contribuyendo al modelo predictor.
El estadístico F es un número alto y p (estadístico F) es casi 0, lo que significa que nuestro modelo es mejor que el único modelo de intersección.
El valor p de la prueba t para la variable de entrada es menor que 0.05, por lo que existe una buena relación entre la variable de entrada y la de salida.
Por lo tanto, concluimos diciendo que nuestro modelo está funcionando bien ✔😊
En este blog, aprendimos los conceptos básicos de Regresión lineal simple (SLR), la construcción de un modelo lineal utilizando diferentes bibliotecas de Python y la elaboración de inferencias de la tabla de resumen de modelos de estadísticas OLS.
Referencias:
Interpretación de la tabla de resumen del modelo de estadísticas OLS
Visualizaciones: Histograma, Gráfico de densidad, trama de violín, diagrama de caja, Gráfico QQ normal, Gráfico de dispersión, gráfico de línea, mapa de calor, trama conjunta
Consulte el cuaderno completo de mi GitHub repositorio.
Espero que este sea un blog informativo para principiantes. Por favor, vote a favor si encuentra esto útil 🙌 Sus comentarios son muy apreciados. Feliz aprendizaje !! 😎
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






