Este artículo fue publicado como parte del Blogatón de ciencia de datos

En este artículo, responderemos estas preguntas básicas y construiremos una red neuronalLas redes neuronales son modelos computacionales inspirados en el funcionamiento del cerebro humano. Utilizan estructuras conocidas como neuronas artificiales para procesar y aprender de los datos. Estas redes son fundamentales en el campo de la inteligencia artificial, permitiendo avances significativos en tareas como el reconocimiento de imágenes, el procesamiento del lenguaje natural y la predicción de series temporales, entre otros. Su capacidad para aprender patrones complejos las hace herramientas poderosas... básica para realizar la regresión lineal.
¿Qué es una red neuronal?
La unidad básica del cerebro se conoce como neurona, hay aproximadamente 86 mil millones de neuronas en nuestro sistema nervioso que están conectadas a 10 ^ 14-10 ^ 15 sinapsis. miCada neurona recibe una señal de las sinapsis y da salida después de procesar la señal. Esta idea se extrae del cerebro para construir una red neuronal.
Cada neurona realiza un producto escalar entre las entradas y los pesos, agrega sesgos, aplica una función de activaciónLa función de activación es un componente clave en las redes neuronales, ya que determina la salida de una neurona en función de su entrada. Su propósito principal es introducir no linealidades en el modelo, permitiendo que aprenda patrones complejos en los datos. Existen diversas funciones de activación, como la sigmoide, ReLU y tanh, cada una con características particulares que afectan el rendimiento del modelo en diferentes aplicaciones.... y emite las salidas. Cuando una gran cantidad de neuronas están presentes juntas para dar una gran cantidad de salidas, se forma una capa neuronal. Finalmente, múltiples capas se combinan para formar una red neuronal.
Arquitectura de red neuronal
Las redes neuronales se forman cuando múltiples capas neuronales se combinan entre sí para dar una red, o podemos decir que hay algunas capas cuyas salidas son entradas para otras capas.
El tipo de capa más común para construir una red neuronal básica es el capa completamente conectada, en el que las capas adyacentes están completamente conectadas por pares y las neuronas de una sola capa no están conectadas entre sí.

En la figura"Figura" es un término que se utiliza en diversos contextos, desde el arte hasta la anatomía. En el ámbito artístico, se refiere a la representación de formas humanas o animales en esculturas y pinturas. En la anatomía, designa la forma y estructura del cuerpo. Además, en matemáticas, "figura" se relaciona con las formas geométricas. Su versatilidad hace que sea un concepto fundamental en múltiples disciplinas.... anterior, las redes neuronales se utilizan para clasificar los puntos de datos en tres categorías.
Convenciones de nombres. Cuando la red neuronal de N capas, no contamos la capa de entradaLa "capa de entrada" se refiere al nivel inicial en un proceso de análisis de datos o en arquitecturas de redes neuronales. Su función principal es recibir y procesar la información bruta antes de que esta sea transformada por capas posteriores. En el contexto de machine learning, una adecuada configuración de la capa de entrada es crucial para garantizar la efectividad del modelo y optimizar su rendimiento en tareas específicas..... Por lo tanto, una red neuronal de una sola capa describe una red sin capas ocultas (la entrada se asigna directamente a la salida). En el caso de nuestro código, vamos a utilizar una red neuronal de una sola capa, es decir, no tenemos una capa oculta.
Capa de salidaLa "capa de salida" es un concepto utilizado en el ámbito de la tecnología de la información y el diseño de sistemas. Se refiere a la última capa de un modelo de software o arquitectura que se encarga de presentar los resultados al usuario final. Esta capa es crucial para la experiencia del usuario, ya que permite la interacción directa con el sistema y la visualización de datos procesados..... A diferencia de todas las capas en una red neuronal, las neuronas de la capa de salida comúnmente no tienen una función de activación (o puede pensar que tienen una función de activación de identidad lineal). Esto se debe a que la última capa de salida generalmente se toma para representar las puntuaciones de la clase (por ejemplo, en la clasificación), que son números arbitrarios de valor real o algún tipo de objetivo de valor real (por ejemplo, en regresión). Dado que estamos realizando la regresión usando una sola capa, no tenemos ninguna función de activación.
Dimensionamiento de redes neuronales. Las dos métricas que la gente usa comúnmente para medir el tamaño de las redes neuronales son el número de neuronas o, más comúnmente, el número de parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto.....
Bibliotecas
Usaremos tres bibliotecas básicas para este modelo, numpy, matplotlib y TensorFlow.
- Numpy: esto agrega soporte para arreglos y matrices grandes y multidimensionales, junto con una gran colección de funciones matemáticas de alto nivel. En nuestro caso, vamos a generar datos con la ayuda de Numpy.
- Matplotlib: esta es una biblioteca de trazado para Python, visualizaremos los resultados finales usando gráficos en Matplotlib.
- Tensorflow: esta biblioteca tiene un enfoque particular en el entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina.... y la inferencia de redes neuronales profundas. Podemos importar directamente las capas y entrenar, probar funciones sin tener que escribir todo el programa.
import numpy as np import matplotlib.pyplot as plt import tensorflow as tf
Generando datos
Podemos generar nuestros propios datos numéricos para este proceso usando la función np.unifrom () que genera datos uniformes. Aquí, estamos usando dos variables de entrada xs y zs, agregando algo de ruido para distribuir aleatoriamente los puntos de datos y, finalmente, la variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... objetivo se define como y = 2 * xs-3 * zs + 5 + ruido. El tamaño del conjunto de datos es 1000.
observations=1000 xs=np.random.uniform(-10,10,(observations,1)) zs=np.random.uniform(-10,10,(observations,1)) generated_inputs=np.column_stack((xs,zs)) noise=np.random.uniform(-10,10,(observations,1)) generated_target=2*xs-3*zs+5+noise
Después de generar los datos, guárdelos en un archivo .npz, para que puedan usarse para entrenamiento.
np.savez('TF_intro',input=generated_inputs,targets=generated_target)
training_data=np.load('TF_intro.npz')Nuestro objetivo es conseguir los pesos finales lo más cerca posible de los pesos reales, es decir [2,-3].
Definiendo el modelo
Aquí, usaremos la capa densaLa capa densa es una formación geológica que se caracteriza por su alta compacidad y resistencia. Comúnmente se encuentra en el subsuelo, donde actúa como una barrera al flujo de agua y otros fluidos. Su composición varía, pero suele incluir minerales pesados, lo que le confiere propiedades únicas. Esta capa es crucial en estudios de ingeniería geológica y recursos hídricos, ya que influye en la disponibilidad y calidad del agua... de TensorFlow para hacer el modelo e importar el descenso del gradienteGradiente es un término utilizado en diversos campos, como la matemática y la informática, para describir una variación continua de valores. En matemáticas, se refiere a la tasa de cambio de una función, mientras que en diseño gráfico, se aplica a la transición de colores. Este concepto es esencial para entender fenómenos como la optimización en algoritmos y la representación visual de datos, permitiendo una mejor interpretación y análisis en... estocástico del optimizador de Keras.
Un gradiente es la pendiente de una función. Mide el grado en que una variable cambia con los cambios de otra variable. Matemáticamente, el descenso de gradiente es una función convexa cuya salida es la derivación parcial de un conjunto de parámetros de sus entradas. Cuanto mayor sea la pendiente, más pronunciada será la pendiente.
A partir de un valor inicial, Gradient Descent se ejecuta iterativamente para encontrar los valores óptimos de los parámetros para encontrar el valor mínimo posible para la función de costo dada. La palabra «estocástico» se refiere a un sistema o proceso de probabilidad aleatorio. Por lo tanto, en Stochastic Gradient Descent, algunas muestras se seleccionan al azar, en lugar del conjunto de datos para cada iteración.
Dado que, la entrada tiene 2 variables, tamaño de entrada = 2 y tamaño de salida = 1.
Establecimos la tasa de aprendizaje en 0.02, que no es ni demasiado alta ni demasiado baja, y el valor de época = 100.
input_size=2
output_size=1
models = tf.keras.Sequential([
tf.keras.layers.Dense(output_size)
])
custom_optimizer=tf.keras.optimizers.SGD(learning_rate=0.02)
models.compile(optimizer=custom_optimizer,loss="mean_squared_error")
models.fit(training_data['input'],training_data['targets'],epochs=100,verbose=1)Obtener pesos y sesgos
Podemos imprimir los valores predichos de pesos y sesgos y también almacenarlos.
models.layers[0].get_weights()
[array([[ 1.3665189],
[-3.1609795]], dtype=float32), array([4.9344487], dtype=float32)]Aquí, la primera matriz representa los pesos y la segunda matriz representa los sesgos. Podemos observar claramente que los valores predichos de los pesos están muy cerca del valor real de los pesos.
weights=models.layers[0].get_weights()[0] bias=models.layers[0].get_weights()[1]
Predicción y precisión
Después de la predicción usando los pesos y sesgos dados, se obtiene una puntuación RMSE final de 0.02866, que es bastante baja.
RMSE se define como el error cuadrático medio de la raíz. El error cuadrático medio toma la diferencia para cada valor observado y predicho. La fórmula para el error RMSE se da como:
https://www.google.com/search?q=rmse+formula&oq=RMSE+form&aqs=chrome.0.0i433j0j69i57j0l7.4779j0j7&sourceid=chrome&ie=UTF-8
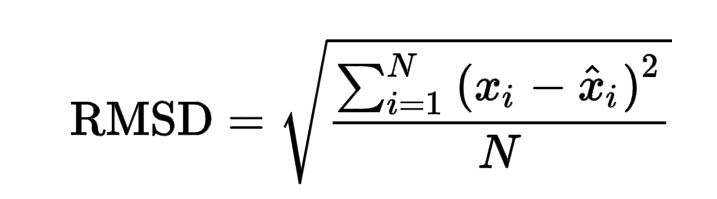
|
| ||
|
| ||
|
| ||
|
|
out=training_data['targets'].round(1) from sklearn.metrics import mean_squared_error mean_squared_error(generated_target, out, squared=False)
Si trazamos los datos predichos en un diagrama de dispersiónEl diagrama de dispersión es una herramienta gráfica utilizada en estadística para visualizar la relación entre dos variables. Consiste en un conjunto de puntos en un plano cartesiano, donde cada punto representa un par de valores correspondientes a las variables analizadas. Este tipo de gráfico permite identificar patrones, tendencias y posibles correlaciones, facilitando la interpretación de datos y la toma de decisiones basadas en la información visual presentada...., obtenemos un gráfico como este:
plt.scatter(np.squeeze(models.predict_on_batch(training_data['input'])),np.squeeze(training_data['targets']),c="#88c999")
plt.xlabel('Input')
plt.ylabel('Predicted Output')
plt.show()
¡Hurra! Nuestro modelo se entrena correctamente con muy pocos errores. Este es el final de su primera red neuronal. Tenga en cuenta que cada vez que entrenamos el modelo podemos obtener un valor diferente de precisión, pero no diferirán mucho.
¡Gracias por leer! Puedes contactar conmigo en [email protected]
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






