Regresión logística R | Introducción a la regresión logística

Visión general

• Obtenga una introducción a la regresión logística usando R y Python
• La regresión logística es un algoritmo de clasificación popular que se utiliza para predecir un resultado binario
• Hay varias métricas para evaluar un modelo de regresión logística, como matriz de confusión, curva AUC-ROC, etc.

Introducción

Cada algoritmo de aprendizaje automático funciona mejor bajo un conjunto de condiciones dado. Asegurarse de que su algoritmo se ajuste a las suposiciones / requisitos garantiza un rendimiento superior. No se puede utilizar ningún algoritmo en ninguna condición. Por ejemplo: ¿Alguna vez ha intentado usar regresión lineal en una variableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... dependiente categórica? ¡Ni lo intentes! Porque no se le apreciará por obtener valores extremadamente bajos de la estadística R² y F ajustada.

En cambio, en tales situaciones, debería intentar usar algoritmos como Regresión logística, Árboles de decisión, SVM, Bosque aleatorio, etc. Para obtener una descripción general rápida de estos algoritmos, recomendaré leer: Conceptos básicos de algoritmos de aprendizaje automático.

Con esta publicación, le proporciono conocimientos útiles sobre la regresión logística en R. Una vez que haya dominado la regresión lineal, este es el siguiente paso natural en su viaje. También es fácil de aprender e implementar, pero debes conocer la ciencia detrás de este algoritmo.

Intenté explicar estos conceptos de la manera más simple posible. Empecemos.

¿Qué es la regresión logística?

La regresión logística es una algoritmo de clasificación. Se utiliza para predecir un resultado binario (1/0, Sí / No, Verdadero / Falso) dado un conjunto de variables independientes. Para representar un resultado binario / categórico, utilizamos variables ficticias. También puede pensar en la regresión logística como un caso especial de regresión lineal cuando la variable de resultado es categórica, donde usamos el logaritmo de probabilidades como variable dependiente. En palabras simples, predice la probabilidad de ocurrencia de un evento ajustando los datos a una función logit.

Derivación de la ecuación de regresión logística

La regresión logística es parte de una clase más amplia de algoritmos conocidos como modelo lineal generalizado (glm). En 1972, Nelder y Wedderburn propusieron este modelo con un esfuerzo por proporcionar un medio de utilizar la regresión lineal para los problemas que no eran directamente adecuados para la aplicación de la regresión lineal. De hecho, propusieron una clase de modelos diferentes (regresión lineal, ANOVA, regresión de Poisson, etc.) que incluían la regresión logística como un caso especial.

La ecuación fundamental del modelo lineal generalizado es:

g(E(y)) = α + βx1 + γx2

Aquí, g () es la función de enlace, E (y) es la expectativa de la variable objetivo y α + βx1 + γx2 es el predictor lineal (α, β, γ por predecir). El papel de la función de enlace es «vincular» la expectativa de y al predictor lineal.

Puntos importantes

1. GLM no asume una relación lineal entre variables dependientes e independientes. Sin embargo, asume una relación lineal entre la función de enlace y las variables independientes en el modelo logit.
2. No es necesario que la variable dependiente se distribuya normalmente.
3. No utiliza OLS (Mínimo cuadrado ordinario) para la estimación de parámetrosLos "parámetros" son variables o criterios que se utilizan para definir, medir o evaluar un fenómeno o sistema. En diversos campos como la estadística, la informática y la investigación científica, los parámetros son fundamentales para establecer normas y estándares que guían el análisis y la interpretación de datos. Su adecuada selección y manejo son cruciales para obtener resultados precisos y relevantes en cualquier estudio o proyecto..... En cambio, utiliza la estimación de máxima verosimilitud (MLE).
4. Los errores deben ser independientes pero no estar distribuidos normalmente.

Entendamos más con un ejemplo:

Se nos proporciona una muestra de 1000 clientes. Necesitamos predecir la probabilidad de que un cliente compre (y) una revista en particular o no. Como puede ver, tenemos una variable de resultado categórica, usaremos regresión logística.

Para comenzar con la regresión logística, primero escribiré la ecuación de regresión lineal simple con la variable dependiente encerrada en una función de enlace:

                           g(y) = βo + β(Age)         ---- (a)

Nota: Para facilitar la comprensión, he considerado ‘Edad’ como variable independiente.

En la regresión logística, solo nos preocupa la probabilidad de la variable dependiente del resultado (éxito o fracaso). Como se describió anteriormente, g () es la función de enlace. Esta función se establece mediante dos cosas: probabilidad de éxito (p) y probabilidad de fracaso (1-p). p debe cumplir con los siguientes criterios:

1. Siempre debe ser positivo (ya que p> = 0)
2. Siempre debe ser menor que igual a 1 (ya que p <= 1)

Ahora, simplemente satisfaceremos estas 2 condiciones y llegaremos al núcleo de la regresión logística. Para establecer la función de enlace, denotaremos g () con ‘p’ inicialmente y eventualmente terminaremos derivando esta función.

Dado que la probabilidad siempre debe ser positiva, pondremos la ecuación lineal en forma exponencial. Para cualquier valor de pendiente y variable dependiente, el exponente de esta ecuación nunca será negativo.

p = exp(βo + β(Age)) = e^(βo + β(Age))    ------- (b)

Para que la probabilidad sea menor que 1, debemos dividir p por un número mayor que p. Esto se puede hacer simplemente mediante:

p  =  exp(βo + β(Age)) / exp(βo + β(Age)) + 1   =   e^(βo + β(Age)) / e^(βo + β(Age)) + 1    ----- (c)

Usando (a), (b) y (c), podemos redefinir la probabilidad como:

              p = e^y/ 1 + e^y           --- (d)

dónde p es la probabilidad de éxito. Esta (d) es la función Logit

Si p es la probabilidad de éxito, 1-p será la probabilidad de fracaso que se puede escribir como:

q = 1 - p = 1 - (e^y/ 1 + e^y)    --- (e)

dónde q es la probabilidad de falla

Al dividir, (d) / (e), obtenemos,

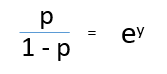
Después de tomar el registro en ambos lados, obtenemos,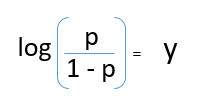

log (p / 1-p) es la función de enlace. La transformación logarítmica de la variable de resultado nos permite modelar una asociación no lineal de forma lineal.

Después de sustituir el valor de y, obtendremos:

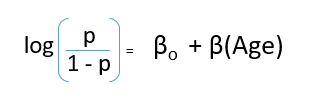
Ésta es la ecuación utilizada en Regresión logística. Aquí (p / 1-p) es la razón impar. Cuando se determina que el logaritmo de la razón impar es positivo, la probabilidad de éxito es siempre superior al 50%. A continuación se muestra un gráfico de modelo logístico típico. Puede ver que la probabilidad nunca desciende por debajo de 0 y por encima de 1.

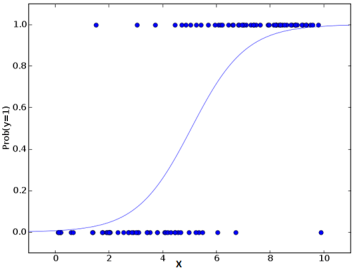
Rendimiento del modelo de regresión logística

Para evaluar el desempeño de un modelo de regresión logística, debemos considerar algunas métricas. Independientemente de la herramienta (SAS, R, Python) en la que trabajaría, busque siempre:

1. AIC (Criterios de información de Akaike) – La métrica análoga de R2 ajustado en regresión logística es AIC. AIC es la medida de ajuste que penaliza al modelo por el número de coeficientes del modelo. Por lo tanto, siempre preferimos el modelo con un valor mínimo de AIC.

2. Desviación nula y desviación residual – La desviación nula indica la respuesta predicha por un modelo con nada más que una intersección. Baje el valor, mejor el modelo. La desviación residual indica la respuesta predicha por un modelo al agregar variables independientes. Baje el valor, mejor el modelo.

3. Matriz de confusión: No es más que una representación tabular de los valores reales frente a los previstos. Esto nos ayuda a encontrar la precisión del modelo y evitar el sobreajuste. Así es como esto luce:

Fuente: (plug – n – score)

Puede calcular el precisión de su modelo con:

De la matriz de confusión, la especificidad y la sensibilidad se pueden derivar como se ilustra a continuación:

La especificidad y la sensibilidad juegan un papel crucial en la derivación de la curva ROC.

4. Curva ROC: La característica operativa del receptor (ROC) resume el rendimiento del modelo mediante la evaluación de las compensaciones entre la tasa de verdaderos positivos (sensibilidad) y la tasa de falsos positivos (1 especificidad). Para graficar ROC, es aconsejable suponer p> 0.5 ya que estamos más preocupados por la tasa de éxito. ROC resume el poder predictivo para todos los valores posibles de p> 0.5. El área bajo la curva (AUC), denominada índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... de precisión (A) o índice de concordancia, es una métrica de rendimiento perfecta para la curva ROC. Cuanto mayor sea el área bajo la curva, mejor será el poder de predicción del modelo. A continuación se muestra una muestra de la curva ROC. La ROC de un modelo predictivo perfecto tiene TP igual a 1 y FP igual a 0. Esta curva tocará la esquina superior izquierda del gráfico.

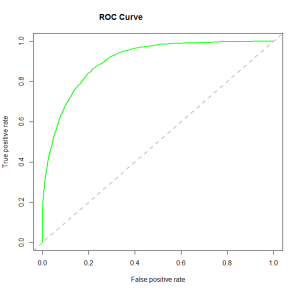
Nota: Para el rendimiento del modelo, también puede considerar la función de probabilidad. Se llama así porque selecciona los valores de los coeficientes que maximizan la probabilidad de explicar los datos observados. Indica bondad de ajuste cuando su valor se acerca a uno y un ajuste deficiente de los datos cuando su valor se acerca a cero.

Modelo de regresión logística en R y Python

El código R se proporciona a continuación, pero si es un usuario de Python, aquí hay una ventana de código increíble para construir su modelo de regresión logística. No es necesario abrir Jupyter, puede hacerlo todo aquí:

Teniendo en cuenta la disponibilidad, construí este modelo en nuestro problema de práctica: el conjunto de datos de Dressify. Puedes descargarlo aquí.

Sin profundizar en la ingeniería de características, aquí está el script del modelo de regresión logística simple:

setwd('C:/Users/manish/Desktop/dressdata')

#load data
train <- read.csv('Train_Old.csv')

#create training and validation data from given data
install.packages('caTools')
library(caTools)

set.seed(88)
split <- sample.split(train$Recommended, SplitRatio = 0.75)

#get training and test data
dresstrain <- subset(train, split == TRUE)
dresstest <- subset(train, split == FALSE)

#logistic regression model
model <- glm (Recommended ~ .-ID, data = dresstrain, family = binomial)
summary(model)

predict <- predict(model, type="response")

#confusion matrix
table(dresstrain$Recommended, predict > 0.5)

#ROCR Curve
library(ROCR)
ROCRpred <- prediction(predict, dresstrain$Recommended)
ROCRperf <- performance(ROCRpred, 'tpr','fpr')
plot(ROCRperf, colorize = TRUE, text.adj = c(-0.2,1.7))

#plot glm
library(ggplot2)
ggplot(dresstrain, aes(x=Rating, y=Recommended)) + geom_point() + 
stat_smooth(method="glm", family="binomial", se=FALSE)

Estos datos requieren mucha limpieza e ingeniería de características. El alcance de este artículo me restringió a mantener el ejemplo enfocado en la construcción del modelo de regresión logística. Estos datos son disponible para practicar. Te recomiendo que trabajes en este problema. Hay mucho que aprender.

Notas finales

A estas alturas, ya conocerá la ciencia detrás de la regresión logística. He visto muchas veces que la gente conoce el uso de este algoritmo sin tener conocimiento sobre sus conceptos centrales. He hecho todo lo posible para explicar esta parte de la manera más simple posible. El ejemplo anterior solo muestra el esqueleto del uso de la regresión logística en R. Antes de acercarse realmente a esta etapa, debe invertir su tiempo crucial en la ingeniería de características.

Además, te recomiendo que trabajes en este conjunto de problemas. Explorarías cosas que quizás no hayas enfrentado antes.

¿Me perdí de algo importante? ¿Le ha resultado útil este artículo? Comparta sus opiniones / pensamientos en la sección de comentarios a continuación.

Si le gusta lo que acaba de leer y desea continuar con su aprendizaje sobre análisis, suscríbete a nuestros correos electrónicos, Síguenos en Twitter o como nuestro pagina de Facebook.

Relacionado