Similitud de imagen | Implementar la similitud de imágenes en Python

Si cree que nuestra imagen de prueba es semejante a nuestra primera imagen de referencia, tiene razón. Si cree lo contrario, averigüémoslo junto con el poder de las matemáticas y la programación.

«El futuro de la búsqueda se centrará en imágenes en lugar de palabras clave». – Ben Silbermann, director ejecutivo de Pinterest.

Vector de imagen

Cada imagen se almacena en nuestra computadora en forma de números y un vector de tales números que puede describir totalmente nuestra imagen se conoce como Vector de Imagen.

Distancia euclidiana:

La distancia euclidiana representa la distancia entre dos puntos cualesquiera en un espacio de n dimensiones. Dado que representamos nuestras imágenes como vectores de imágenes, no son más que un punto en un espacio de n dimensiones y vamos a utilizar la distancia euclidiana para hallar la distancia entre ellos.

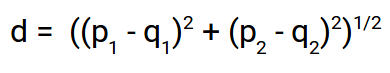
Histograma:

Un histograma es una visualización gráfica de valores numéricos. Usaremos el vector de imagen para las tres imágenes y después hallaremos la distancia euclidiana entre ellas. Según los valores devueltos, la imagen con una distancia menor es más semejante que la otra.

Para hallar la similitud entre las dos imágenes, usaremos el siguiente enfoque:

1. Lea los archivos de imagen como una matriz.
2. Dado que los archivos de imagen están coloreados, hay 3 canales para los valores RGB. Los vamos a aplanar de modo que cada imagen sea una única matriz 1-D.
3. Una vez que tengamos nuestros archivos de imagen como una matriz, vamos a generar un histograma para cada imagen donde para cada índice 0-255 vamos a contar la ocurrencia de ese valor de píxel en la imagen.
4. Una vez que tengamos nuestros histogramas, usaremos la regla L2 o la distancia euclidiana para hallar la diferencia entre los dos histogramas.
5. Basándonos en la distancia entre el histograma de nuestra imagen de prueba y las imágenes de referencia, podemos hallar la imagen a la que nuestra imagen de prueba es más semejante.

Codificación para la similitud de imágenes en Python

Importar las dependencias que vamos a usar

from PIL import Image
from collections import Counter
import numpy as np

Usaremos NumPy para guardar la imagen como una matriz NumPy, Image para leer la imagen en términos de valores numéricos y Counter para contar el número de veces que ocurre cada valor de píxel (0-255) en las imágenes.

Leer la imagen

reference_image_1 = Image.open('Reference_image1.jpg')
reference_image_arr = np.asarray(reference_image_1)
print(np.shape(reference_image_arr))
>>> (250, 320, 3)

Podemos ver que nuestra imagen se ha leído correctamente como una matriz 3-D. En el siguiente paso, debemos aplanar esta matriz 3-D en una matriz unidimensional.

flat_array_1 = array1.flatten()
print(np.shape(flat_array_1))
>>> (245760, )

Vamos a hacer los mismos pasos para las otras dos imágenes. Lo omitiré aquí para que puedas probarlo además.

Generación del vector de histograma de conteo:

RH1 = Counter(flat_array_1)

La próxima línea de código devuelve un diccionario donde la clave corresponde al valor del píxel y el valor de la clave es el número de veces que ese píxel está presente en la imagen.

Una limitación de la distancia euclidiana es que necesita que todos los vectores estén normalizados, dicho de otra forma, ambos vectores deben tener las mismas dimensiones. Para asegurarnos de que nuestro vector de histograma esté normalizado, usaremos un bucle for de 0-255 y generaremos nuestro histograma con el valor de la clave si la clave está presente en la imagen; caso contrario, agregamos un 0.

H1 = []
for i in range(256):
    if i in RH1.keys():
        H1.append(RH1[i])
    else:
        H1.append(0)

El fragmento de código anterior genera un vector de tamaño (256,) donde cada índiceEl "Índice" es una herramienta fundamental en libros y documentos, que permite ubicar rápidamente la información deseada. Generalmente, se presenta al inicio de una obra y organiza los contenidos de manera jerárquica, incluyendo capítulos y secciones. Su correcta elaboración facilita la navegación y mejora la comprensión del material, convirtiéndolo en un recurso esencial tanto para estudiantes como para profesionales en diversas áreas.... corresponde al valor del píxel y el valor corresponde al recuento del píxel en esa imagen.

Seguimos los mismos pasos para las otras dos imágenes y obtenemos sus correspondientes Conteo-Histograma-Vectores. En este punto, tenemos nuestros vectores finales tanto para las imágenes de referencia como para la imagen de prueba y todo lo que haremos es calcular las distancias y predecir.

Función de distancia euclidiana:

def L2Norm(H1,H2):
    distance =0
    for i in range(len(H1)):
        distance += np.square(H1[i]-H2[i])
    return np.sqrt(distance)

La función anterior toma dos histogramasLos histogramas son representaciones gráficas que muestran la distribución de un conjunto de datos. Se construyen dividiendo el rango de valores en intervalos, o "bins", y contando cuántos datos caen en cada intervalo. Esta visualización permite identificar patrones, tendencias y la variabilidad de los datos de manera efectiva, facilitando el análisis estadístico y la toma de decisiones informadas en diversas disciplinas.... y devuelve la distancia euclidiana entre ellos.

Evaluación:

Como tenemos todo lo que necesitamos para hallar las semejanzas de la imagen, averigüemos la distancia entre la imagen de prueba y nuestra primera imagen de referencia.

dist_test_ref_1 = L2Norm(H1,test_H)
print("The distance between Reference_Image_1 and Test Image is : {}".format(dist_test_ref_1))
>>> The distance between Reference_Image_1 and Test Image is : 9882.175468994668

Averigüemos ahora la distancia entre la imagen de prueba y nuestra segunda imagen de referencia.

dist_test_ref_2 = L2Norm(H2,test_H)
print("The distance between Reference_Image_2 and Test Image is : {}".format(dist_test_ref_2))
>>> The distance between Reference_Image_2 and Test Image is : 137929.0223122023

Conclusión

Según los resultados anteriores, podemos ver que la distancia entre nuestra imagen de prueba y nuestra primera imagen de referencia es mucho menor que la distancia entre nuestra prueba y nuestra segunda imagen de referencia, lo cual tiene sentido debido a que tanto la imagen de prueba como nuestra primera imagen de referencia son imágenes de Piegon mientras que nuestra segunda imagen de referencia es de un pavo real.

En el siguiente tutorial, aprendimos cómo utilizar matemáticas básicas y poca programación para construir nuestro propio predictor de similitud de imágenes con resultados bastante decentes.

Se puede hallar el código completo junto con las imágenes. aquí.

Sobre el Autor

Mi nombre es Prateek Agrawal y soy un estudiante de tercer año en el Instituto Indio de Diseño y Fabricación de Tecnología de la Información Kancheepuram, cursando mi B.Tech y M.Tech Dual Degree en Ciencias de la Computación. Siempre he tenido un don para el aprendizaje automático y la ciencia de datos y lo he estado practicando a lo largo del último año y además tengo algunas victorias en mi haber.

Yo personalmente creo que La pasión es todo lo que necesitas. Recuerdo que me asusté al escuchar a la gente hablar sobre CNNS, RNN y Deep Learning debido a que no podía comprender ni una sola parte, pero no me rendí. Tenía la pasión y comencé a dar pequeños pasos hacia el aprendizaje y aquí estoy publicando mi primer blog. Espero que hayas disfrutado leyendo esto y te sientas un poco seguro de ti mismo. Confía en mí en esto, si puedo, tú puedes.

Por favor, escríbame en caso de cualquier consulta o simplemente para saludar.

LinkedIn: https://www.linkedin.com/in/prateekagrawal1405/
Github: https://github.com/prateekagrawaliiit

Créditos

• Wikipedia
• AnalíticaLa analítica se refiere al proceso de recopilar, medir y analizar datos para obtener información valiosa que facilite la toma de decisiones. En diversos campos, como los negocios, la salud y el deporte, la analítica permite identificar patrones y tendencias, optimizar procesos y mejorar resultados. El uso de herramientas avanzadas y técnicas estadísticas es fundamental para transformar datos en conocimiento aplicable y estratégico.... Vidhya
• Medio
• Imágenes de Google