Introducción
Todos los modelos son incorrectos, pero algunos son útiles – George Box
El análisis de regresión marca el primer paso en el modelado predictivo. Sin duda, es bastante fácil de implementar. Ni su sintaxis ni sus parámetros crean ningún tipo de confusión. Pero, simplemente ejecutar solo una línea de código, no resuelve el propósito. Ni solo mirando los valores R² o MSE. ¡La regresión dice mucho más que eso!
En R, el análisis de regresión devuelve 4 gráficos usando plot(model_name) función. Cada una de las tramas proporciona información significativa o más bien una historia interesante sobre los datos. Lamentablemente, muchos de los principiantes no logran descifrar la información o no les importa lo que dicen estas tramas. Una vez que comprenda estos gráficos, podrá aportar una mejora significativa en su modelo de regresión.
Para mejorar el modelo, también debe comprender los supuestos de regresión y las formas de corregirlos cuando se infringen.
En este artículo, he explicado las suposiciones y gráficos importantes de regresión (con correcciones y soluciones) para ayudarlo a comprender el concepto de regresión con más detalle. Como se dijo anteriormente, con este conocimiento puede traer mejoras drásticas en sus modelos.
Nota: Para comprender estos gráficos, debe conocer los conceptos básicos del análisis de regresión. Si es completamente nuevo en él, puede comenzar aquí. Luego, continúe con este artículo.
Supuestos en regresión
La regresión es un enfoque paramétrico. ‘Paramétrico’ significa que hace suposiciones sobre los datos con fines de análisis. Debido a su lado paramétrico, la regresión es de naturaleza restrictiva. No ofrece buenos resultados con conjuntos de datos que no cumplen sus suposiciones. Por lo tanto, para un análisis de regresión exitoso, es esencial validar estos supuestos.
Entonces, ¿cómo comprobaría (validaría) si un conjunto de datos sigue todos los supuestos de regresión? Lo verifica utilizando los gráficos de regresión (explicados a continuación) junto con alguna prueba estadística.
Veamos los supuestos importantes en el análisis de regresión:
- Debe haber una relación lineal y aditiva entre la variable dependiente (respuesta) y la variable independiente (predictora). Una relación lineal sugiere que un cambio en la respuesta Y debido al cambio de una unidad en X¹ es constante, independientemente del valor de X¹. Una relación aditiva sugiere que el efecto de X¹ en Y es independiente de otras variables.
- No debe haber correlación entre los términos residuales (error). La ausencia de este fenómeno se conoce como autocorrelación.
- Las variables independientes no deben estar correlacionadas. La ausencia de este fenómeno se conoce como multicolinealidad.
- Los términos de error deben tener una varianza constante. Este fenómeno se conoce como homocedasticidad. La presencia de varianza no constante se refiere a heterocedasticidad.
- Los términos de error deben distribuirse normalmente.
¿Qué pasa si se violan estas suposiciones?
Analicemos suposiciones específicas y aprendamos sobre sus resultados (si se violan):
1. Lineal y aditivo: Si ajusta un modelo lineal a un conjunto de datos no lineales y no aditivos, el algoritmo de regresión no capturaría la tendencia matemáticamente, lo que resultaría en un modelo ineficiente. Además, esto resultará en predicciones erróneas en un conjunto de datos invisible.
Como revisar: Busque gráficas de valor residual vs ajustado (explicado a continuación). Además, puede incluir términos polinomiales (X, X², X³) en su modelo para capturar el efecto no lineal.
2. Autocorrelación: La presencia de correlación en términos de error reduce drásticamente la precisión del modelo. Esto suele ocurrir en modelos de series de tiempo donde el siguiente instante depende del instante anterior. Si los términos de error están correlacionados, los errores estándar estimados tienden a subestimar el verdadero error estándar.
Si esto sucede, hace que los intervalos de confianza y los intervalos de predicción sean más estrechos. Un intervalo de confianza más estrecho significa que un intervalo de confianza del 95% tendría una probabilidad menor que 0,95 de contener el valor real de los coeficientes. Comprendamos los intervalos de predicción estrechos con un ejemplo:
Por ejemplo, el coeficiente de mínimos cuadrados de X¹ es 15.02 y su error estándar es 2.08 (sin autocorrelación). Pero en presencia de autocorrelación, el error estándar se reduce a 1,20. Como resultado, el intervalo de predicción se reduce a (13.82, 16.22) desde (12.94, 17.10).
Además, los errores estándar más bajos harían que los valores p asociados fueran más bajos que los reales. Esto nos hará concluir incorrectamente que un parámetro es estadísticamente significativo.
Como revisar: Busque la estadística de Durbin-Watson (DW). Debe estar entre 0 y 4. Si DW = 2, no implica autocorrelación, 0 <DW <2 implica autocorrelación positiva mientras que 2 <DW <4 indica autocorrelación negativa. Además, puede ver el gráfico residual frente al tiempo y buscar el patrón estacional o correlacionado en los valores residuales.
3. Multicolinealidad: Este fenómeno existe cuando se encuentra que las variables independientes tienen una correlación moderada o alta. En un modelo con variables correlacionadas, se vuelve una tarea difícil averiguar la verdadera relación de un predictor con una variable de respuesta. En otras palabras, resulta difícil averiguar qué variable contribuye realmente a predecir la variable de respuesta.
Otro punto, con presencia de predictores correlacionados, los errores estándar tienden a aumentar. Y, con grandes errores estándar, el intervalo de confianza se vuelve más amplio, lo que conduce a estimaciones menos precisas de los parámetros de pendiente.
Además, cuando los predictores están correlacionados, el coeficiente de regresión estimado de una variable correlacionada depende de qué otros predictores estén disponibles en el modelo. Si esto sucede, terminará con una conclusión incorrecta de que una variable afecta fuerte / débilmente a la variable objetivo. Dado que, incluso si elimina una variable correlacionada del modelo, sus coeficientes de regresión estimados cambiarían. ¡Eso no es bueno!
Como revisar: Puede utilizar el diagrama de dispersión para visualizar el efecto de correlación entre las variables. Además, también puede utilizar el factor VIF. El valor de VIF = 10 implica una multicolinealidad seria. Sobre todo, una tabla de correlaciones también debería resolver el propósito.
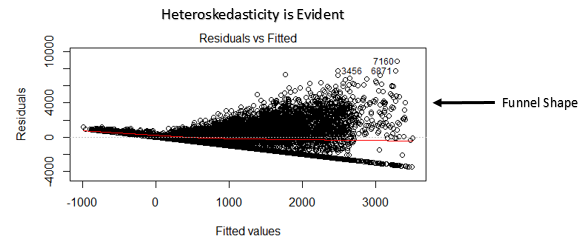
4. Heteroscedasticidad: La presencia de varianza no constante en los términos de error da como resultado heterocedasticidad. Generalmente, la varianza no constante surge en presencia de valores atípicos o valores de apalancamiento extremos. Parece que estos valores tienen demasiado peso, por lo que influyen de manera desproporcionada en el rendimiento del modelo. Cuando ocurre este fenómeno, el intervalo de confianza para la predicción fuera de muestra tiende a ser irrealmente amplio o estrecho.
Como revisar: Puede ver la gráfica de valores residuales frente a ajustados. Si existe heterocedasticidad, la gráfica exhibirá un patrón en forma de embudo (que se muestra en la siguiente sección). Además, puede utilizar la prueba de Breusch-Pagan / Cook – Weisberg o la prueba general de White para detectar este fenómeno.
5. Distribución normal de términos de error: Si los términos de error no se distribuyen normalmente, los intervalos de confianza pueden volverse demasiado amplios o estrechos. Una vez que el intervalo de confianza se vuelve inestable, se dificulta la estimación de coeficientes basados en la minimización de mínimos cuadrados. La presencia de una distribución anormal sugiere que hay algunos puntos de datos inusuales que deben estudiarse de cerca para hacer un mejor modelo.
Como revisar: Puede ver el gráfico QQ (que se muestra a continuación). También puede realizar pruebas estadísticas de normalidad como la prueba de Kolmogorov-Smirnov, la prueba de Shapiro-Wilk.
Interpretación de gráficos de regresión
Hasta aquí, hemos aprendido acerca de los supuestos de regresión importantes y los métodos a emprender, si esos supuestos se violan.
Pero ese no es el final. Ahora, debe conocer las soluciones también para abordar la violación de estos supuestos. En esta sección, he explicado las 4 gráficas de regresión junto con los métodos para superar las limitaciones de los supuestos.
1. Valores residuales frente a valores ajustados
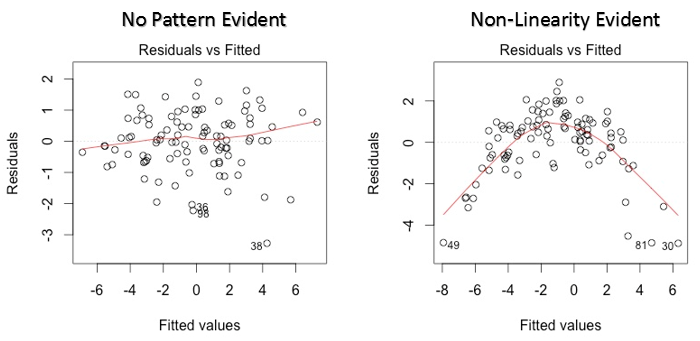
Este gráfico de dispersión muestra la distribución de los residuos (errores) frente a los valores ajustados (valores predichos). Es una de las tramas más importantes que todo el mundo debe aprender. Revela varios conocimientos útiles, incluidos los valores atípicos. Los valores atípicos en este gráfico están etiquetados por su número de observación, lo que los hace fáciles de detectar.
Hay dos cosas importantes que debes aprender:
- Si existe algún patrón (puede ser, una forma parabólica) en este gráfico, considérelo como signos de no linealidad en los datos. Significa que el modelo no captura efectos no lineales.
- Si la forma de un embudo es evidente en el gráfico, considérelo como un signo de varianza no constante, es decir, heterocedasticidad.
Solución: Para superar el problema de la no linealidad, puede hacer una transformación no lineal de predictores como log (X), √X o X² transforman la variable dependiente. Para superar la heterocedasticidad, una posible forma es transformar la variable de respuesta como log (Y) o √Y. Además, puede utilizar el método de mínimos cuadrados ponderados para abordar la heterocedasticidad.
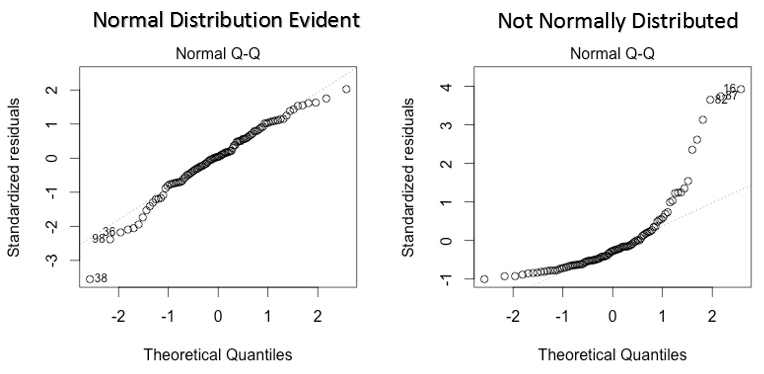
2. Gráfico QQ normal
Este qq o cuantil-cuantil es un diagrama de dispersión que nos ayuda a validar el supuesto de distribución normal en un conjunto de datos. Usando esta gráfica podemos inferir si los datos provienen de una distribución normal. En caso afirmativo, la gráfica mostraría una línea bastante recta. Se aprecia ausencia de normalidad en los errores con desviación en línea recta.
Si se pregunta qué es un ‘cuantil’, aquí tiene una definición simple: piense en los cuantiles como puntos en sus datos por debajo de los cuales cae una cierta proporción de datos. El cuantil se denomina a menudo percentiles. Por ejemplo: cuando decimos que el valor del percentil 50 es 120, significa que la mitad de los datos está por debajo de 120.
Solución: Si los errores no se distribuyen normalmente, la transformación no lineal de las variables (respuesta o predictores) puede traer una mejora en el modelo.
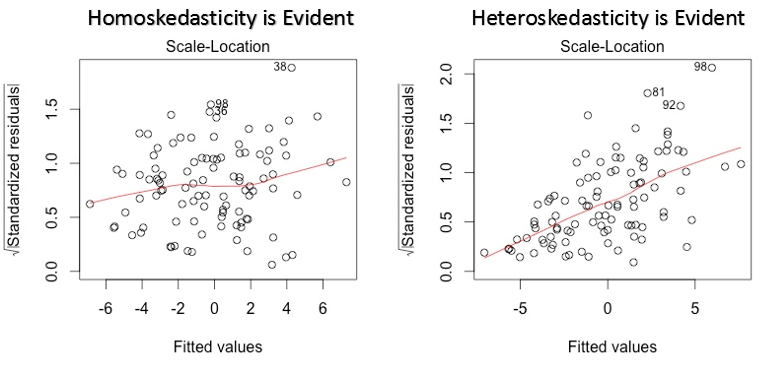
3. Gráfico de ubicación de escala
Esta gráfica también se usa para detectar homocedasticidad (supuesto de varianza igual). Muestra cómo se distribuyen los residuales a lo largo del rango de predictores. Es similar a la gráfica de valor residual vs ajustado excepto que usa valores residuales estandarizados. Idealmente, no debería haber un patrón discernible en la trama. Esto implicaría que los errores se distribuyen normalmente. Pero, en caso de que la gráfica muestre algún patrón discernible (probablemente una forma de embudo), implicaría una distribución de errores no normal.
Solución: Siga la solución para heterocedasticidad dada en la gráfica 1.
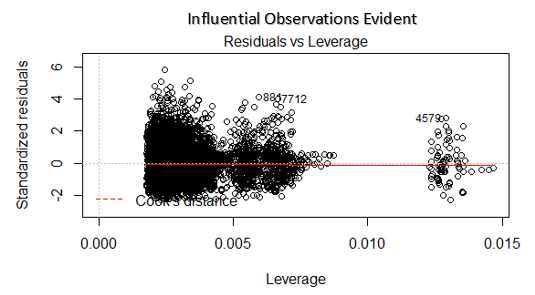
4. Gráfico de residuos vs apalancamiento
También se conoce como diagrama de distancia de Cook. La distancia de Cook intenta identificar los puntos que tienen más influencia que otros puntos. Tales puntos influyentes tienden a tener un impacto considerable en la línea de regresión. En otras palabras, agregar o eliminar dichos puntos del modelo puede cambiar completamente las estadísticas del modelo.
Pero, ¿se pueden tratar estas influyentes observaciones como valores atípicos? Esta pregunta solo se puede responder después de mirar los datos. Por lo tanto, en este gráfico, los valores grandes marcados por la distancia de cocción pueden requerir una mayor investigación.
Solución: Para observaciones influyentes que no son más que valores atípicos, si no muchos, puede eliminar esas filas. Alternativamente, puede reducir la observación de valores atípicos con el valor máximo en los datos o tratar esos valores como valores perdidos.
Caso de estudio: Cómo mejoré mi modelo de regresión usando la transformación logarítmica
Notas finales
Puede aprovechar el verdadero poder del análisis de regresión aplicando las soluciones descritas anteriormente. Implementar estas correcciones en R es bastante fácil. Si desea conocer alguna solución específica en R, puede dejar un comentario, estaré encantado de ayudarlo con las respuestas.
El motivo de este artículo fue ayudarlo a obtener el conocimiento y la perspectiva subyacentes de los supuestos y diagramas de regresión. De esta manera, tendrá más control sobre su análisis y podrá modificar el análisis según sus necesidades.
¿Le resultó útil este artículo? ¿Ha utilizado estas correcciones para mejorar el rendimiento del modelo? Comparta su experiencia / sugerencias en los comentarios.