Teoría de la decisión bayesiana | Introducción a la teoría de la decisión bayesiana

Este post fue difundido como parte del Blogatón de ciencia de datos

Introducción

Teoría de la decisión bayesiana se refiere al enfoque estadístico basado en la cuantificación de compensaciones entre varias decisiones de clasificación sustentadas en el concepto de probabilidad (Teorema de Bayes) y los costos asociados con la decisión.

Simplemente es una técnica de clasificación que implica el uso del Teorema de Bayes que se utiliza para hallar las probabilidades condicionales.

En Acreditación de patrones estadísticos, nos centraremos en las propiedades estadísticas de los patrones que de forma general se expresan en densidades de probabilidad (pdf y pmf), y esto atraerá la mayor parte de nuestra atención en este post y tratará de desarrollar los argumentos de la teoría de la decisión bayesiana.

Prerrequisitos

VariableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria

Una variable aleatoria es una función que asigna un factible conjunto de resultados a algunos valores, como al lanzar una moneda y obtener la cara H como 1 y la cola T como 0, donde 0 y 1 son variables aleatorias.

Teorema de Bayes

La probabilidad condicional de A dado B, representada por P (A | B) es la probabilidad de que ocurra A dado que B ha ocurrido.

P (A | B) = P (A, B) / P (B) o

Al utilizar la regla de la cadena, esto además se puede escribir como:

P (A, B) = P (A | B) P (B) = P (B | A) P (A)

P (A | B) = P (B | A) P (A) / P (B) ——- (1)

Dónde, P (B) = P (B, A) + P (B, A ‘) = P (B | A) P (A) + P (B | A’) P (A ‘)

Aquí, la ecuación (1) se conoce como Teorema de probabilidad de Bayes

Nuestro objetivo es explorar cada uno de los componentes incluidos en este teorema. Exploremos paso a paso:

(a) Previo o Estado de Naturaleza:

• Las probabilidades previas representan la probabilidad de que ocurra cada clase.
• Los anteriores se conocen antes del procedimiento de capacitación.
• El estado de la naturaleza es una variable aleatoria P (w_I).
• Si solo hay dos clases, entonces la suma de los anteriores es P (w₁) + P (w₂) = 1, si las clases son exhaustivas.

(b) Probabilidades condicionales de clase:

• Representa la probabilidad de la probabilidad de que ocurra una característica x dado que pertenece a la clase particular. Se denota por, P (X | A) donde x es una característica particular
• Es la probabilidad de la probabilidad de que ocurra la característica x dado que pertenece a la clase w_I.
• A veces, además se conoce como Probabilidad.
• Es la cantidad que tenemos que examinar mientras entrenamos los datos. A lo largo del procedimiento de entrenamientoEl entrenamiento es un proceso sistemático diseñado para mejorar habilidades, conocimientos o capacidades físicas. Se aplica en diversas áreas, como el deporte, la educación y el desarrollo profesional. Un programa de entrenamiento efectivo incluye la planificación de objetivos, la práctica regular y la evaluación del progreso. La adaptación a las necesidades individuales y la motivación son factores clave para lograr resultados exitosos y sostenibles en cualquier disciplina...., tenemos la entrada (características) X etiquetada a la clase respectivo w y calculamos la probabilidad de ocurrencia de ese conjunto de características dada la etiqueta de la clase.

(c) Evidencia:

• Es la probabilidad de que ocurra una característica en particular, dicho de otra forma P (X).
• Se puede calcular usando la regla de la cadena como, P (X) = Σ_en P (X | w_I) P (w_I)
• Como necesitamos la probabilidad de probabilidad condicional de clase, además se calculan los valores de evidencia a lo largo del entrenamiento.

(d) Probabilidades posteriores:

• Es la probabilidad de que ocurra la clase A cuando se dan ciertas características.
• Es lo que pretendemos calcular en la etapa de prueba en la que tenemos entrada de prueba o características (la entidad dada) y tenemos que hallar qué tan probable es que el modelo entrenado pueda predecir características que pertenecen a la clase particular w_I.

Para una mejor comprensión de la teoría anterior, consideramos un ejemplo

Descripción del problema

Supongamos que tenemos un enunciado de un obstáculo de clasificación en el que tenemos que categorizar entre el objeto 1 y el objeto 2 con el conjunto de características dado. X = [x₁, x₂, …, x_n]^T.

Objetivo

El objetivo principal de diseñar un clasificador de este tipo es sugerir acciones cuando se presentan con características invisibles, dicho de otra forma, un objeto aún no visto, dicho de otra forma, no en los datos de entrenamiento.

En este ejemplo, w denota el estado de naturaleza con w = w₁ para objeto-1 y w = w₂ para objeto-2. Aquí, necesitamos saber que en realidad, el estado de naturaleza es tan impredecible que de forma general consideramos que fue variable la que se describe probabilísticamente.

Priors

• De forma general, asumimos que existe algún valor previo P (w₁) que el siguiente objeto es object-1 y P (w₂) que el siguiente objeto es object-2. Si no tenemos otro objeto como en este problema, entonces la suma de sus anteriores es 1, dicho de otra forma, los anteriores son exhaustivos.
• Las probabilidades previas reflejan el conocimiento previo de la probabilidad de que obtengamos el objeto 1 y el objeto 2. Depende del dominio, puesto que el anterior puede cambiar según la época del año en que se detecta.

Suena un poco extraño y al juzgar múltiples objetos (como en un escenario más realista) hace que esta regla de decisión sea estúpida puesto que siempre tomamos la misma decisión basándonos en el mayor anterior aún cuando sabemos que cualquier otro tipo de objetivo además podría aparecer regido por el probabilidades previas sobrantes (puesto que las anteriores son de naturaleza exhaustiva).

Considere los siguientes escenarios diferentes:

• Si P (ω₁) >>> P (ω₂), nuestra decisión a favor de ω₁ será correcto la mayor parte del tiempo que predecimos.
• Pero si P (ω₁) = P (ω₂), medio probable de nuestra predicción de estar en lo cierto. En general, la probabilidad de error es el mínimo de P (ω₁) y P (ω₂), y más adelante en este post, veremos que bajo estas condiciones ninguna otra regla de decisión puede producir una mayor probabilidad de ser correcta.

Procedimiento de extracción de características (Extraer característica de las imágenes)

Un conjunto de características sugeridas Largo, ancho, alternativas para un objetoetc.

En nuestro ejemplo, usamos el ancho x, Cual es más discriminatorio para impulsar la regla de decisión de nuestro clasificador. Los diferentes objetos producirán diferentes lecturas de ancho variable y de forma general vemos esta variabilidad en términos probabilísticos y además consideramos que x es una variable aleatoria continua cuya distribución depende del tipo de objeto w_j, y se expresa como p (x | ω_j) (función de distribución de probabilidad pdf como una variable continua) y conocida como función de densidad de probabilidad condicional de clase. Por eso,

El pdf p (x | ω₁) es la función de densidad de probabilidad para la característica x dado que el estado de la naturaleza es ω₁ y la misma interpretación para p (x | w₂).

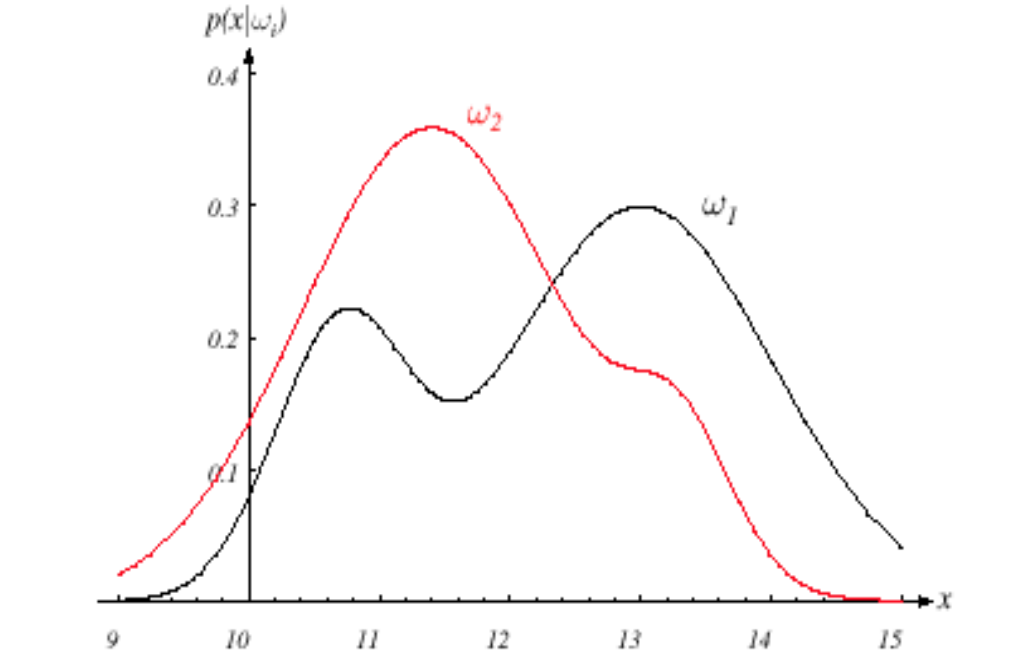
Fig. Imagen que muestra pdf para ambas clases

Fuente de la imagen: imágenes de Google

Suponga que conocemos bien las probabilidades previas P (ω_j) y las densidades condicionales p (x | ω_j). Ahora, podemos llegar a la fórmula de Bayes para hallar probabilidades posteriores:

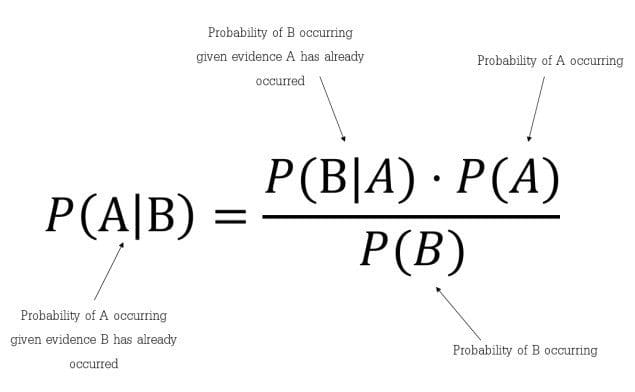
Fig. Fórmula del teorema de Bayes

Fuente de la imagen: imágenes de Google

La fórmula de Bayes nos da la intuición de que al observar la medidaLa "medida" es un concepto fundamental en diversas disciplinas, que se refiere al proceso de cuantificar características o magnitudes de objetos, fenómenos o situaciones. En matemáticas, se utiliza para determinar longitudes, áreas y volúmenes, mientras que en ciencias sociales puede referirse a la evaluación de variables cualitativas y cuantitativas. La precisión en la medición es crucial para obtener resultados confiables y válidos en cualquier investigación o aplicación práctica.... de x podemos convertir la P (ω_j) a los posteriores, denotado por P (ω_j| x) que es la probabilidad de ω_j dado que se ha medido el valor de característica x.

p (x | ω_j) se conoce como probabilidad de ω_j con respecto ax.

El factor de evidencia, p (x), funciona simplemente como un factor de escala que garantiza que las probabilidades posteriores sumen uno para todas las clases.

Regla de decisión de Bayes

La regla de decisión dadas las probabilidades posteriores es la próxima

Si P (w₁| x)> P (w₂| x) decidiríamos que el objeto pertenece a la clase w₁, o caso contrario clase w₂.

Probabilidad de error

Para justificar nuestra decisión, miramos la probabilidad de error, siempre que observemos x, tenemos,

P (error | x) = P (w₁| x) si decidimos w₂, y P (w₂| x) si decidimos w₁

Como son exhaustivos y si elegimos la naturaleza correcta de un objeto por probabilidad P, entonces la probabilidad sobrante (1-P) mostrará qué tan probable es la decisión de que no es el objeto decidido.

Podemos minimizar la probabilidad de error decidiendo cuál tiene un posterior mayor y el resto puesto que la probabilidad de error será la mínima factible. Por lo tanto para terminar obtenemos

P (error | x) = min [P(ω₁|x),P(ω₂|x)]

Y nuestra regla de decisión de Bayes como,

Elegir ω₁ si P (ω₁| x)> P (ω₂| x); caso contrario decide ω₂

Este tipo de regla de decisión destaca el papel de las probabilidades posteriores. Con la ayuda del teorema de Bayes, podemos expresar la regla en términos de probabilidades condicionales y previas.

Las pruebas carecen de relevancia en lo que respecta a la decisión. Como comentamos previamente, funciona simplemente como un factor de escala que indica la frecuencia con la que mediremos la característica con el valor x; asegura P (ω₁| x) + P (ω₂| x) = 1.

Entonces, al borrar el factor de escala no requerido en nuestra regla de decisión, tenemos la regla de decisión semejante del teorema de Bayes como,

Elegir ω₁ si p (x | ω₁) P (ω₁)> p (x | ω₂) P (ω₂); caso contrario decide ω₂

Ahora, consideremos 2 casos:

• Caso 1: Si los condicionales de clase son iguales, dicho de otra forma, p (x | ω₁) = p (x | ω₂), llegamos entonces a nuestra regla de decisión prematura regida por justos a priori.
• Caso 2: Por otra parte, si los anteriores son iguales, dicho de otra forma, P (ω₁) = P (ω₂) entonces la decisión se basa enteramente en condicionales de clase p (x | ω_j).

¡Esto completa nuestra formulación de ejemplo!

Generalización de las ideas anteriores para clases y características múltiples

Clasificación de Bayes: posterior, verosimilitud, previa y evidencia

P (w_I | X) = P (X | w_I) P (w_I) / P (X)

Posterior = Probabilidad * Previo / Evidencia

Ahora discutimos aquellos casos que disponen múltiples características, así como múltiples clases,

Deje que las características múltiples sean X₁, X₂, … X_norte y múltiples clases sean w₁, w₂,… W_norte, después:

P (w_I | X₁,…. X_norte) = P (X₁,…. , X_norte| w_I) * P (w_I) / P (X₁,… X_norte)

Dónde,

Posterior = P (w_I | X₁,…. X_norte)

Probabilidad = P (X₁,…. , X_norte| w_I)

Previo = P (w_I)

Evidencia = P (X₁,… ,X_norte)

En casos de los mismos patrones entrantes, es factible que necesitemos utilizar una función de costo drásticamente distinto, lo que conducirá a acciones absolutamente diferentes. De forma general, diferentes tareas de decisión pueden requerir características y límites de rendimiento bastante diferentes de los útiles para nuestro problema de categorización original.

Entonces, en los posts posteriores, discutiremos el Función de costo, Análisis de riesgo, y acción decisiva lo que ayudará a comprender mejor la teoría de la decisión de Bayes.

Notas finales

¡Gracias por leer!

Si le gustó esto y quiere saber más, visite mis otros posts sobre ciencia de datos y aprendizaje automático haciendo clic en el Link

No dude en ponerse en contacto conmigo en Linkedin, Email.

¿Algo no mencionado o deseas compartir tus pensamientos? No dude en comentar a continuación y me pondré en contacto con usted.

Sobre el Autor

Chirag Goyal

Hoy en día, estoy cursando mi Licenciatura en Tecnología (B.Tech) en Ciencias de la Computación e Ingeniería de la Instituto Indio de Tecnología de Jodhpur (IITJ). Estoy muy entusiasmado con el aprendizaje automático, el aprendizaje profundoEl aprendizaje profundo, una subdisciplina de la inteligencia artificial, se basa en redes neuronales artificiales para analizar y procesar grandes volúmenes de datos. Esta técnica permite a las máquinas aprender patrones y realizar tareas complejas, como el reconocimiento de voz y la visión por computadora. Su capacidad para mejorar continuamente a medida que se le proporcionan más datos la convierte en una herramienta clave en diversas industrias, desde la salud... y la inteligencia artificial.

Los medios que se muestran en este post no son propiedad de DataPeaker y se usan a discreción del autor.

Relacionado