
Introducción a los conceptos básicos de la teoría de la probabilidad
Averigüe la probabilidad de que obtenga una bola negra o roja. Tenga en cuenta que denotaremos probabilidad como P a partir de ahora. P (X) significa la probabilidad de que ocurra un evento X.
P (bola roja) = P (bolsa A). P (Bola roja | Bolsa A) + P (Bolsa B). P (Bola roja | Bolsa B), esta ecuación calcula la probabilidad de la bola roja. Aquí he introducido el concepto de la probabilidad condicional (que encuentra la probabilidad cuando se nos proporciona la condición). P (Bolsa A) = 1/2 porque tenemos 2 bolsas que tenemos que seleccionar Bolsa A. P (Bola roja | Bolsa A) debe leer como «probabilidad de sacar una bola roja dado la bolsa A«Aquí» la palabra «dada» especifica la condición que es la Bolsa A en este caso, por lo que son 10 bolas rojas de 20 bolas, es decir, 10/20. Así que resolvamos:
P (bola roja) = 1/2. 10/20 + 1/2. 10/20 = 1/2
De manera similar, ¿puedes intentar encontrar la probabilidad de sacar una bola negra? Además, calcule la probabilidad de sacar dos bolas rojas consecutivas de la bolsa después de transferir una bola negra de la bolsa A a la bolsa B.

Ahora, si miras la imagen de arriba, debes estar pensando ¿qué es? No he introducido la «intersección» en la teoría de conjuntos. Ya he discutido el concepto anterior, no hay nada nuevo en la imagen dada arriba. Aquí estamos encontrando la probabilidad de que ocurra un evento A dado que el evento B ya ocurrió. El numerador del lado derecho de la ecuación es la probabilidad de que ocurran ambos eventos, dividida por la probabilidad de que ocurra un evento B. El numerador tiene un símbolo de forma invertida entre A y B que llamamos «Intersección» en la teoría de conjuntos.
Introducción al teorema de Bayes
Hasta ahora, acabamos de discutir los conceptos básicos de la teoría de la probabilidad. Antes de continuar, déjame discutir ‘VariableEn estadística y matemáticas, una "variable" es un símbolo que representa un valor que puede cambiar o variar. Existen diferentes tipos de variables, como las cualitativas, que describen características no numéricas, y las cuantitativas, que representan cantidades numéricas. Las variables son fundamentales en experimentos y estudios, ya que permiten analizar relaciones y patrones entre diferentes elementos, facilitando la comprensión de fenómenos complejos.... aleatoria‘que es una variable cuyos posibles valores son resultados numéricos de un fenómeno aleatorio. En el caso anterior, Bag es una variable aleatoria que puede tomar valores posibles como Bag A y Bag B. Ball también es una variable aleatoria que puede tomar valores rojo y negro.
Ahora imagina la situación anterior cuando digo hallar la probabilidad de que la bola se saque de una bolsa A dado que la bola es de color rojo. Observe que en esta pregunta ya se nos ha dado el color de la bola y tenemos que encontrar la probabilidad de que la bola roja sea sacada de la bolsa A. En cambio, en otras preguntas usamos para encontrar la probabilidad de sacar una bola roja de bolsa A. En el caso de que tengamos que encontrar la probabilidad del evento y se da el objeto, este tipo de probabilidad se llama probabilidad posterior. En el caso de que tengamos que encontrar la probabilidad de un objeto dado para ese evento, este tipo de probabilidad se conoce como probabilidad previa. Entonces, la respuesta a mi pregunta al principio del párrafo es:
P (Bolsa A | bola roja) = [P(red ball | Bag A). P(Bag A) ] / [P(red ball | Bag A). P(Bag A) + P(red ball | Bag B). P(Bag B) ]
La ecuación anterior es lo que llamamos “Teorema de Bayes”, uno de los teoremas más significativos e importantes dados por el Reverendo Thomas Bayes.
Ahora, quiero que eche un vistazo a lo que estudiamos hasta ahora sobre eventos discretos. En el aprendizaje automático, generalmente necesitamos eventos ‘continuos’ en lugar de una variable discreta. ¿Qué hacemos ahora? ¡Mire la imagen que se muestra a continuación e intente comprender entre los dos tipos de eventos de los que acabo de hablar!
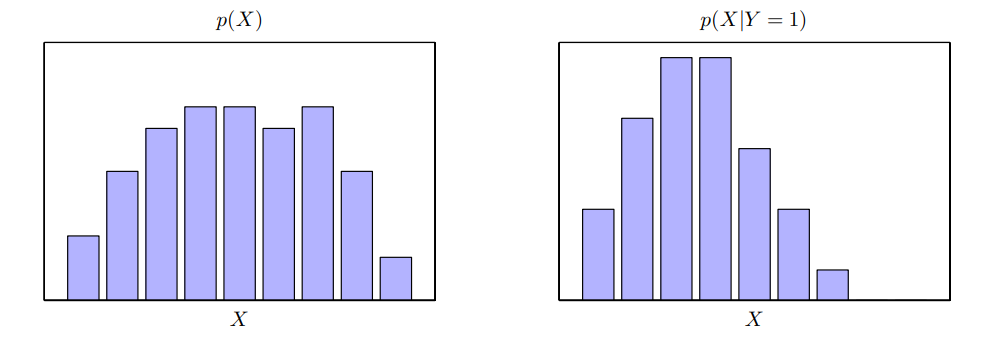
¿Qué es la densidad de probabilidad?
Como les dije, estábamos considerando las probabilidades de eventos discretos, pero nuestro requisito es para eventos continuos. Para lograr esto, me gustaría introducir el concepto de «densidad de probabilidad» aquí en este punto. Sea la probabilidad de x con valor real dentro del intervalo (x, x + dx) dada por la integral de p (x) .dx donde dx–> 0, entonces p (x) es la densidad de probabilidad sobre x. La probabilidad de x se encuentra en el intervalo [a,b] viene dada por la integral de aab de p (x) .dx. Esto se muestra en la imagen que se muestra a continuación.
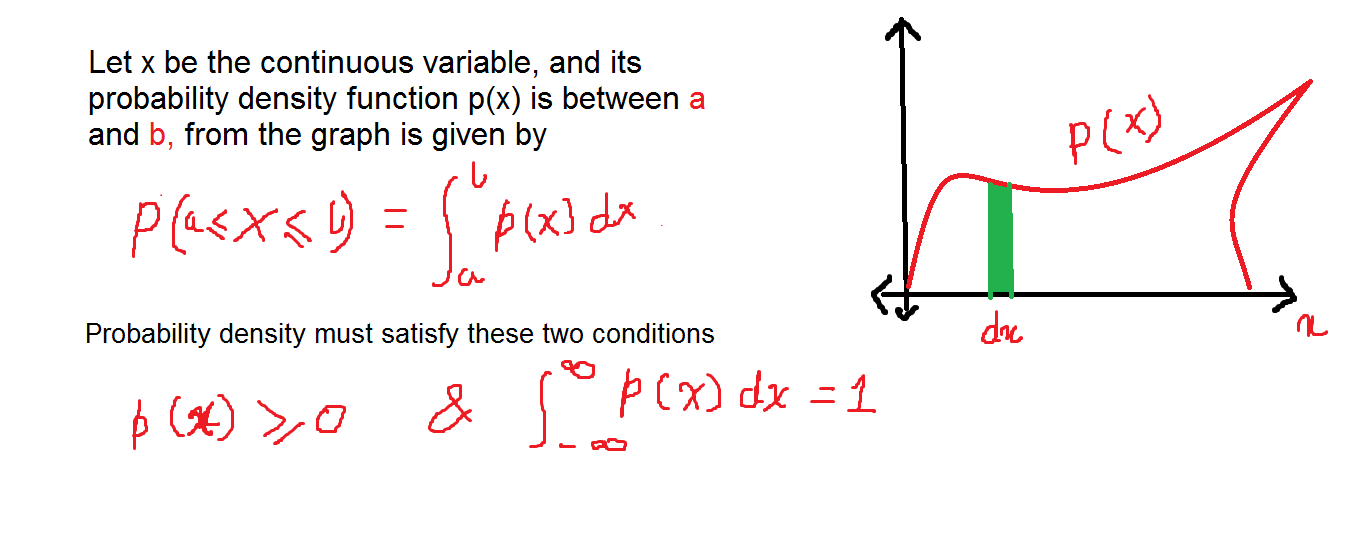
Si miras la imagen, también he especificado las dos condiciones que debe satisfacer la densidad de probabilidad.
¡Excelente! Aprendiste algo que es muy difícil de una manera mucho más fácil. ¿No es así?
¿Cómo se relaciona con el aprendizaje automático?
Entonces, aprendimos los conceptos básicos de la teoría de la probabilidad, pero aún así, ¿estamos confundidos acerca de cómo relacionamos esto con el aprendizaje automático? ¿No es así? Usamos la probabilidad cuando tenemos que hacer predicciones. Cuando tenemos el modelo en ML y los datos, podemos usarlo para hacer predicciones basadas en el modelo entrenado. Considere un caso en el que tenemos un conjunto de datos para diferentes temperaturas en una región para diferentes fechas. Aquí podemos hacer predicciones sobre cuántas botellas de agua se deben almacenar en esa región con la ayuda de un modelo.
He tratado de cubrir todo lo que puedo en este artículo, pero hay mucho que aprender en la teoría de la probabilidad. Es solo lo básico. Hasta ahora, acabamos de discutir la definición de probabilidad, la probabilidad condicional, el teorema de Bayes y la densidad de probabilidad. ¡¡Buena suerte!!
Los medios que se muestran en este artículo no son propiedad de DataPeaker y se utilizan a discreción del autor.






