Dieser Artikel wurde im Rahmen der Data Science Blogathon

Einführung
Lernen. Die logistische Regression wird im Allgemeinen verwendet, wenn wir die Daten in zwei oder mehr Klassen einteilen müssen. Eine ist binär und die andere ist eine logistische Regression mit mehreren Klassen. Wie der Name schon sagt, die binäre klasse hat 2 Klassen, die ja sind / Nein, Wahr / Gefälscht, 0/1, etc. Bei der Klassifizierung mehrerer Klassen, es gibt mehr von 2 Klassen zum Klassifizieren von Daten. Aber, bevor wir gehen, definieren wir zuerst die logistische Regression:
„Die logistische Regression ist ein Klassifizierungsalgorithmus für kategoriale Variablen wie Ja / Nein, Wahr / Gefälscht, 0/1, etc.“
Wie unterscheidet sie sich von der linearen Regression??
Vielleicht haben Sie auch schon von linearer Regression gehört. Lassen Sie mich Ihnen sagen, dass es einen großen Unterschied zwischen linearer Regression und logistischer Regression gibt. Lineare Regression wird verwendet, um kontinuierliche Werte wie den Preis des Hauses zu generieren, Einkommen, die Bevölkerung, etc. In der logistischen Regression, berechnen wir im Allgemeinen die Wahrscheinlichkeit, die zwischen dem Intervall . liegt 0 Ja 1 (beide inklusive). Dann kann die Wahrscheinlichkeit verwendet werden, um die Daten zu klassifizieren. Zum Beispiel, wenn die berechnete Wahrscheinlichkeit größer als ist 0,5, dann gehörten die Daten zur Klasse A und, andererseits, für weniger als 0,5, die Daten gehörten zur Klasse B.
Aber meine Frage ist, ob wir die lineare Regression noch zur Klassifizierung verwenden können. Meine Antwort wird sein: „Ja!! Warum nicht? Aber es ist sicher eine absurde Idee". Mein Grund wird sein, dass Sie einen Schwellenwert für die lineare Regression zuweisen können, nämlich, wenn der vorhergesagte Wert größer als der Schwellenwert ist, gehörte zur Klasse A; andererseits, zur Klasse B. Aber es wird ein großer Fehler und ein schlechtes Modell mit geringer Präzision geben, das wollen wir wirklich nicht. Rechts? Ich schlage vor, Sie verwenden nur Sortieralgorithmen.
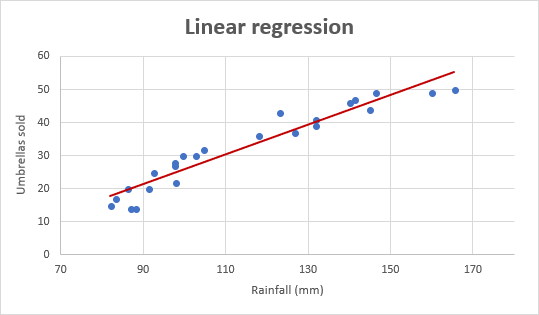
Schauen wir uns nun das unten gezeigte lineare Regressionsdiagramm an.
(Höflichkeit: https://www.ablebits.com/)
Der Graph ist eine gerade Linie, die durch einige Punkte geht, da wir immer Überanpassungen und Fehlanpassungen von Kurven vermeiden.
Werfen wir nun einen Blick auf den logistischen Regressionsgraphen:
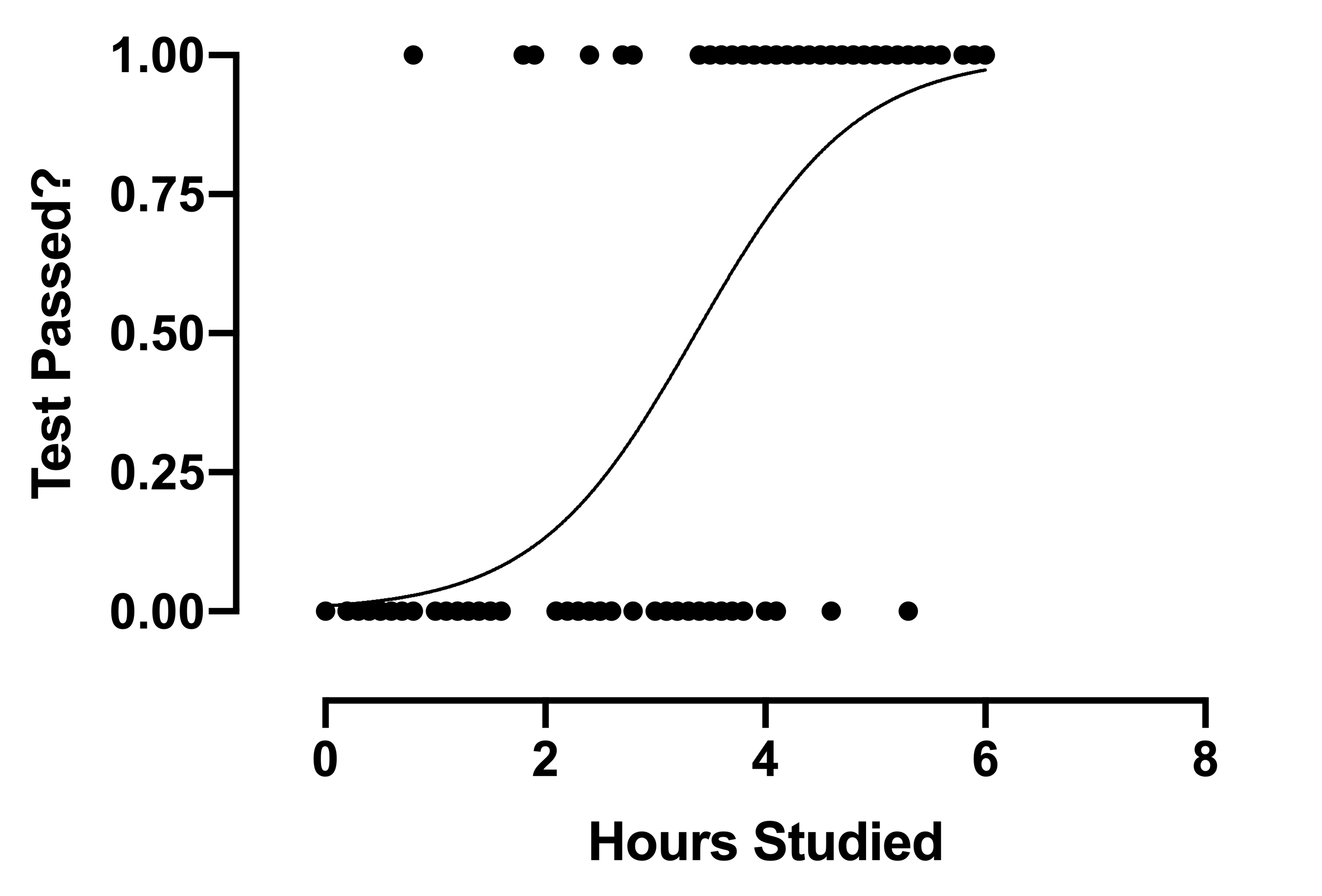
Der Graph ist eine gekrümmte Linie statt einer geraden Linie, im Gegensatz zur linearen Regression.
Dies ist ein großer Unterschied zwischen den beiden Regressionsarten, über die wir gerade gesprochen haben.. Also meine nächste Frage ist.
Warum haben wir eine gekrümmte Linie für die logistische Regression anstelle einer geraden??
Um diese Frage zu beantworten, Wir werden ein wenig durch die lineare Regression gehen und von dort aus zur logistischen Regressionskurve kommen. Das ist in Ordnung? Lasst uns beginnen.
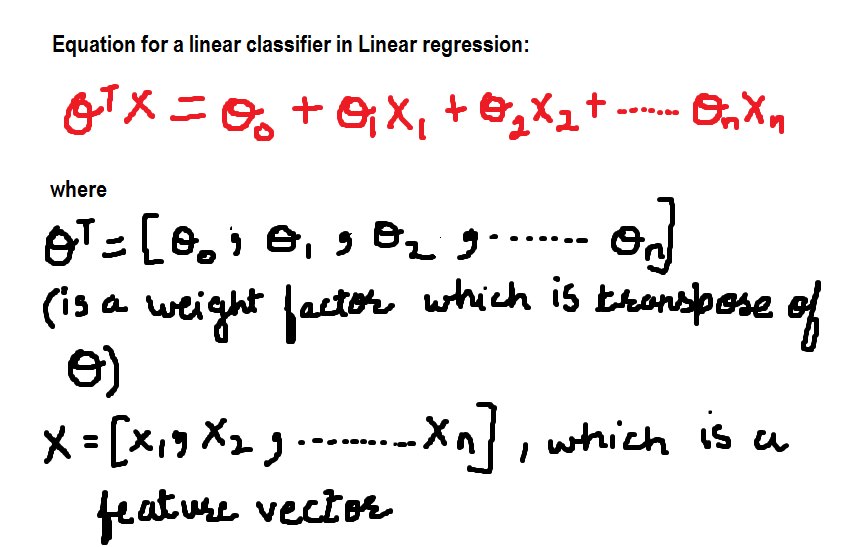
Zur Zeit, die Gleichung für den linearen Klassifikator ist:
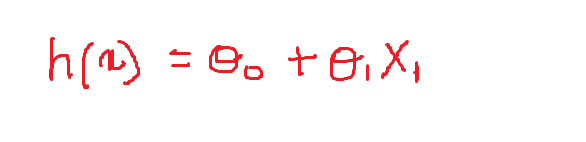
Jetzt definieren wir die Werte der variablen Gewichte:
theta_0 = -1 und theta = 0.1
Dann, Unsere Gleichung sieht so aus und das folgende ist der Graph, der die Gleichung in der 2D-Ebene darstellt:
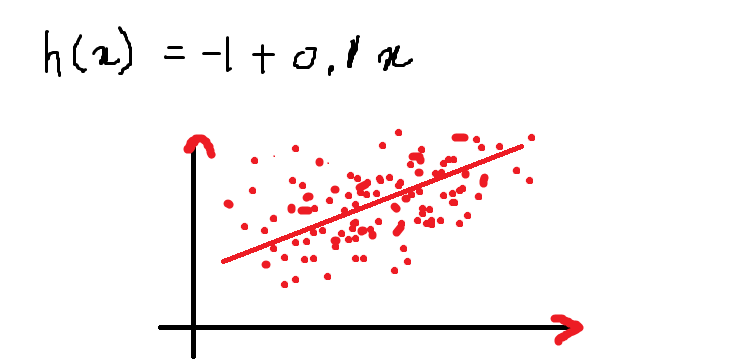
Oben ist eine Geradengleichung für die gegebene Gleichung:
h (x) = – 1 + 0.1x
Der Wert der Funktion h (x) wenn x = 13 es ist:
h (13) = – 1+ (0,1) * (13) = 0,3
Wie bereits in diesem Artikel beschrieben, Ich definiere die Schwelle in 0.5, das ist ein beliebiger Wert von h größer als (gleicht) 0.5 wird beschriftet als 1 Ja, andererseits, 0. Wir können es wie folgt in Form einer Stufenfunktion definieren:

Jetzt, stimme dem zu, h hat einen Wert von 0.3, daher der Wert von y_hat = 0 nach der oben definierten Funktion.
Jetzt, Hier ist zu beachten, dass jeder Wert größer als 0.5, suponga que digo que el valor de ‚h‘ es ist 1000 für einen Wert von x, dann wird es beschriftet als 1 nur, es gibt keinen Unterschied zwischen dem Wert 1 Ja 1000 da beide klassifiziert sind als 1 nur. Es ist richtig? Können wir diese Lösung akzeptieren?? Nun, nein! würde ich nicht akzeptieren !!!
Eine Sache noch, Wie groß ist die Wahrscheinlichkeit, dass h den Wert hat 0.3? All diese Fragen bleiben unbeantwortet. Aus diesen Gründen, Datenwissenschaftler ziehen es nicht vor, lineare Regression für Klassifizierungszwecke zu verwenden.
vor dem Fortfahren, Ich möchte Ihnen zeigen, wie sich die Funktion y_hat grafisch verhält:
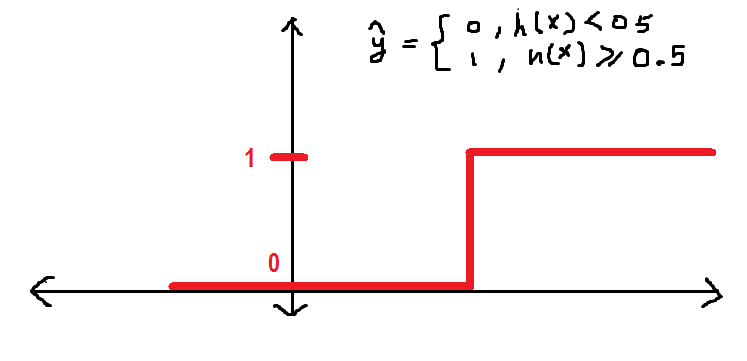
Es ist besser, wenn wir eine glattere Kurve anstelle der oben genannten haben. Wir werden sehen:
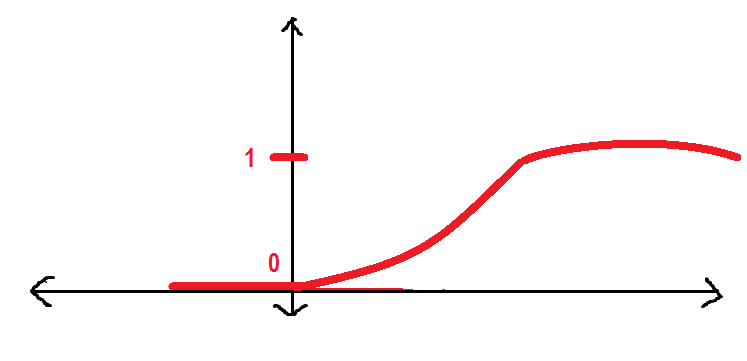
Die obige Kurve ist bekannt als Sigmoid-Funktion die wir in diesem Artikel verwenden werden. Hier stelle ich die Sigmoidfunktion vor.
Was ist die Sigmoidfunktion??
Die Sigmoidfunktion wird durch das Symbol sigma . dargestellt. Su comportamiento gráfico se ha descrito en la Abbildung"Abbildung" ist ein Begriff, der in verschiedenen Zusammenhängen verwendet wird, Von der Kunst zur Anatomie. Im künstlerischen Bereich, bezieht sich auf die Darstellung menschlicher oder tierischer Formen in Skulpturen und Gemälden. In der Anatomie, bezeichnet die Form und Struktur des Körpers. Was ist mehr, in der Mathematik, "Abbildung" Es hängt mit geometrischen Formen zusammen. Seine Vielseitigkeit macht es zu einem grundlegenden Konzept in mehreren Disziplinen.... anterior. Die mathematische Gleichung für die Sigmoidfunktion wird unten beschrieben:
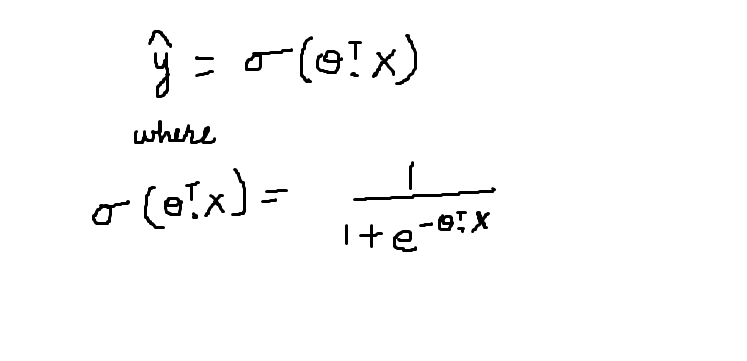
Die Sigmoidfunktion gibt die Wahrscheinlichkeit an, dass die Daten zu einer bestimmten Klasse gehören, die im Intervall liegt [0,1]. Akzeptiert das Skalarprodukt der Transposition von Theta und dem Merkmalsvektor X als Parameter. Der resultierende Wert ist die Wahrscheinlichkeit.
Deswegen, Wenn P (Y = 1 | x) = Sigmoide (theta * x)
P (Y = 0 | x) = 1- sigmoide (theta * x)
Was ist mehr, Ich möchte, dass Sie das Verhalten der Sigmoidfunktion beobachten:
- Wenn theta (Umsetzung) * X wird so viel größer, der Sigmoidwert wird gleich 1
- Wann theta (Umsetzung) * X wird sehr klein, der Sigmoidwert wird gleich 0
Anwendungen der logistischen Regression
In diesem Abschnitt, Ich möchte einige der Anwendungen der logistischen Regression diskutieren.
1. Vorhersage der Wahrscheinlichkeit, dass eine Person einen Herzinfarkt erleidet
2. Vorhersage der Neigung eines Kunden, ein Produkt zu kaufen oder ein Abonnement auszusetzen.
3. Vorhersage der Ausfallwahrscheinlichkeit eines bestimmten Prozesses oder Produkts.
Bevor Sie diesen Artikel beenden, Ich möchte nur zusammenfassen, wann Sie logistische Regression verwenden sollten:
- Wenn Ihre Daten binär sind: 0/1, Wahr / Gefälscht, Jawohl / Nein
- Wenn Sie probabilistische Ergebnisse benötigen
- Wenn Ihre Daten linear getrennt werden können
- Wenn Sie die Auswirkungen der Funktion verstehen müssen.
Neben der logistischen Regression werden viele andere Klassifikationsalgorithmen wie kNN . verwendet, Entscheidungsbäume, Random Forest und Clustering-Algorithmen als Clustering von k-Means. Aber die logistische Regression ist ein weit verbreiteter Algorithmus und auch einfach zu implementieren..
Es ging also um den logistischen Regressionsalgorithmus für Anfänger. Wir haben über alles gesprochen, was Sie über die logistische Regressionstheorie wissen müssen. Ich hoffe, Ihnen hat mein Artikel gefallen!!
Die in diesem Artikel gezeigten Medien sind nicht Eigentum von DataPeaker und werden nach Ermessen des Autors verwendet.
Verwandt
zusammenhängende Posts:
- Logistische Regression R | Einführung in die logistische Regression
- Logistische Regression | Ein Anfängerleitfaden zur logistischen Regression mit Python
- Lineare vs. logistische Regression | Lineare und logistische Regression
- Lineare Regression | Einführung in die lineare Regression für Data Science