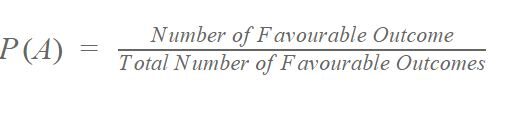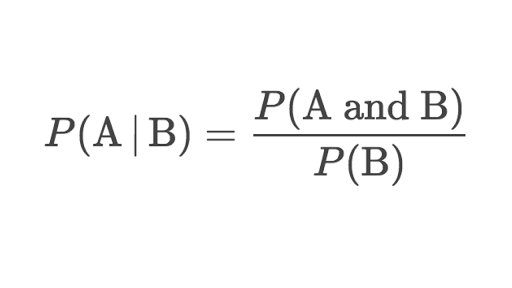Statistik ist die Grammatik der Wissenschaft.
– Karl Pearson
Was sind Daten??
Daten sind Informationen, die aus verschiedenen Quellen gesammelt werden, die qualitativer oder quantitativer Natur sein können.. Meist, die gesammelten Daten werden verwendet, um Informationen zu einem bestimmten Thema zu analysieren und zu erhalten.
Zum Beispiel:
1. Zylindergröße, Kilometerstand, Farbe, etc. für den Verkauf eines Autos
2.Ob Zellen im Körper bösartig oder gutartig sind, um Krebs zu erkennen
Art der Daten
Numerische Daten
Numerische Daten sind Informationen in Zahlen, nämlich, numerisch, das als quantitatives Maß der Dinge dargestellt wird.
Zum Beispiel:
- Körpergrößen und Gewichte von Personen
- Aktienkurse
ein) Diskrete Daten
Diskrete Daten sind die Informationen, die oft von einem Ereignis erzählen, nämlich, kann nur bestimmte Werte annehmen. Sie basieren oft auf ganzen Zahlen, aber nicht unbedingt.
Zum Beispiel:
- Wie oft eine Münze geworfen wurde
- Menschen Schuhgrößen
B) Kontinuierliche Daten
Kontinuierliche Daten sind Informationen, die die Möglichkeit haben, unendliche Werte zu haben, nämlich, kann jeden Wert innerhalb eines Bereichs annehmen.
Zum Beispiel:
Wie viele Zentimeter Regen fielen an einem bestimmten Tag?
Kategoriale Daten
Diese Art von Daten ist qualitativer Natur und hat keine inhärente mathematische Bedeutung.. Es ist eine Art fester Wert, unter dem es zugewiesen wird oder “kategorisieren” eine Beobachtungseinheit.
Zum Beispiel:
- Geschlecht
- Binärdaten (Jawohl / Nein)
- Attribute eines Fahrzeugs als Farbe, Kilometerstand, Anzahl der Türen, etc.
Ordnungsdaten
Dieser Datentyp ist die Kombination aus numerischen und kategorialen Daten, nämlich, kategoriale Daten, die eine mathematische Bedeutung haben.
Zum Beispiel:
Restaurantbewertungen von 1 ein 5, Sein 1 die niedrigste und 5 das höchste
STATISTIKEN:
Medien, mittel und modus
Meinen
In Mathematik und Statistik, der Mittelwert ist der Durchschnitt der numerischen Beobachtungen, der gleich der Summe der Beobachtungen dividiert durch die Anzahl der Beobachtungen ist.
wo,
 |
= | Bedeutung arithmetisch |
 |
= | Anzahl der Werte |
 |
= | Datensatzwerte |
Median
Der Median der Daten, bei aufsteigender oder absteigender Sortierung, ist die zentrale Beobachtung der Daten, nämlich, der Punkt, der die obere Hälfte von der unteren Hälfte der Daten trennt.
Um den Median zu berechnen:
- Organisieren Sie Ihre Daten in aufsteigender oder absteigender Reihenfolge.
- eine ungerade Anzahl von Datenpunkten: der Mittelwert ist der Median.
- gerade Anzahl Datenpunkte: der Durchschnitt der beiden Mittelwerte ist der Median.
 |
= | eine geordnete Liste von Werten im Datensatz |
 |
= | Anzahl der Werte im Datensatz |
Weg
das Weg einer Menge von Datenpunkten ist der häufigste Wert.
Zum Beispiel:
5, 2,6,5, 1,1,2,5, 3,8,5, 9,5 sind die Datenpunkte. Hier 5 ist die Art weil es häufiger vorkommt.
Varianz und Standardabweichung
Unterschied
Mathematisch und statistisch, Unterschied ist definiert als der Durchschnitt der quadrierten Differenzen vom Mittelwert. Aber um es zu verstehen, das beschreibt wie erweitert die Daten sind in einem Datensatz.
Die Schritte zur Berechnung der Varianz anhand eines Beispiels:
Finden wir die Varianz von (1,4,5,4,8)
- Ermitteln Sie den Mittelwert der Datenpunkte nämlich (1 + 4 + 5 + 4 + 8) / 5 = 4.4
- Finde die Unterschiede mit dem Mittelwert nämlich (-3,4, -0,4, 0,6, -0,4, 3,6)
- Finde die Differenzen im Quadrat nämlich (11,56, 0,16, 0,36, 0,16, 12,96)
- Ermitteln Sie den Durchschnitt der quadrierten Differenzen nämlich, 11,56 + 0,16 + 0,36 + 0,16 + 12,96 / 5 = 5,04
Die Formel für dasselbe ist:
Standardabweichung
Die Standardabweichung misst die Variation oder Streuung von Datenpunkten in einem Datensatz. Stellt die Nähe des Datenpunkts zum Mittelwert dar und wird als Quadratwurzel der Varianz berechnet.
In der Datenwissenschaft, Standardabweichung wird im Allgemeinen verwendet, um Ausreißer in einem Datensatz zu identifizieren. Datenpunkte, die innerhalb einer Standardabweichung vom Mittelwert liegen, gelten als ungewöhnlich.
Die Formel für die Standardabweichung lautet:
 |
= | Bevölkerungsstandardabweichung |
 |
= | die Größe der Bevölkerung |
 |
= | jeder Bevölkerungswert |
 |
= | die Bevölkerung meint |
Bevölkerungsdaten V / s Beispieldaten
Bevölkerungsdaten bezieht sich auf den kompletten Datensatz, während Beispieldaten bezieht sich auf einen Teil der Bevölkerungsdaten, der für die Analyse verwendet wird. Die Probenahme erfolgt, um die Analyse zu erleichtern.
Bei Verwendung von Beispieldaten zur Analyse, die Abweichungsformel ist etwas anders. Bei insgesamt n Stichproben, wir teilen durch n-1 statt n:
 |
= | Stichprobenabweichung |
 |
= | der Wert einer Beobachtung |
 |
= | der Mittelwert der Beobachtungen |
 |
= | die Anzahl der Beobachtungen |
WAHRSCHEINLICHKEIT:
Was ist Wahrscheinlichkeit?
Das Konzept der Wahrscheinlichkeit ist extrem einfach. Es bedeutet die Wahrscheinlichkeit des Eintretens eines Ereignisses oder die Wahrscheinlichkeit des Eintretens eines Ereignisses.
Die Wahrscheinlichkeitsformel lautet:
Zum Beispiel:
Die Wahrscheinlichkeit, dass die Münze beim Werfen Kopf zeigt, beträgt 0,5.
Die bedingte Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, solange ein anderes Ereignis bereits eingetreten ist.
Die bedingte Wahrscheinlichkeitsformel:
Zum Beispiel:
Die Schüler einer Klasse haben zwei Prüfungen im Fach Mathematik abgelegt. Im ersten Test, das 60% der Schüler passieren, während nur die 40% der Schüler bestehen beide Prüfungen. Wie viel Prozent der Schüler haben den ersten Test bestanden?, sie haben den zweiten test bestanden?
Teorema de Bayes
Der Satz von Bayes ist ein sehr wichtiges statistisches Konzept, das in vielen Branchen verwendet wird., wie Gesundheit und Finanzen. Die bedingte Wahrscheinlichkeitsformel, die wir zuvor erstellt haben, wurde ebenfalls aus diesem Satz abgeleitet.
Wird verwendet, um die Wahrscheinlichkeit einer Hypothese basierend auf den Wahrscheinlichkeiten verschiedener Daten zu berechnen, die in der Hypothese bereitgestellt werden.
Die Formel des Satzes von Bayes lautet:
 |
= | Veranstaltungen |
 |
= | Wahrscheinlichkeit von A gegeben B ist wahr |
 |
= | Wahrscheinlichkeit von B bei gegebenem A ist wahr |
 |
= | die unabhängigen Wahrscheinlichkeiten von A und B |
Zum Beispiel:
Angenommen, es gibt einen HIV-Test, der HIV-Patienten identifizieren kann + positiv genau die 99% der Zeiten, und das hat auch ein negatives Ergebnis mit Genauigkeit für die 99% von HIV-negativen Menschen. Hier, nur der 0,3% der Gesamtbevölkerung ist seropositiv.
FAZIT
Die im Artikel behandelten Themen zu Statistik und Wahrscheinlichkeit sind wirklich wichtig, aber es gibt noch viele andere Themen wie Wahrscheinlichkeitsverteilungsfunktionen und ihre Typen, Kovarianz und Korrelation, etc., die hier nicht behandelt wurden, da sie aufgrund ihrer Grafik gesondert behandelt werden müssen. Natur.
Mathematik und Statistik sind das Herzstück der Data Science. Die in diesem Artikel behandelten Themen sind die Grundlage vieler Algorithmen, Formeln zur Fehlerberechnung und zum grafischen Verständnis der Dinge, sie sind also sehr wichtig und können nicht ignoriert werden.
