Dieser Artikel wurde im Rahmen der Data Science Blogathon
Agenda
Wir alle haben irgendwann in unserem Leben eine logistische Regression aufgebaut. Auch wenn wir noch nie ein Modell gebaut haben, wir haben diese prädiktive Modellierungstechnik definitiv theoretisch gelernt. Zwei einfache und unterbewertete Konzepte, die im Vorverarbeitungsschritt zum Aufbau eines logistischen Regressionsmodells verwendet werden, sind Beweiskraft und Informationswert.. Ich möchte sie mit diesem Artikel wieder ins Rampenlicht rücken..
Dieser Artikel ist wie folgt aufgebaut:
- Einführung in die logistische Regression
- Bedeutung der Funktionsauswahl
- Bedarf an einem guten Imputer für kategoriale Merkmale
- GEBRECHEN
- NS
Lasst uns beginnen!
1. Einführung in die logistische Regression
Das Erste ist das Erste, Wir alle wissen, dass die logistische Regression ein Klassifizierungsproblem ist. Speziell, wir betrachten hier die binären Klassifikationsprobleme.
Die logistischen Regressionsmodelle verwenden sowohl kategoriale als auch numerische Daten als Eingabe und geben die Eintrittswahrscheinlichkeit des Ereignisses aus.
Beispiele für Problemstellungen, die mit dieser Methode gelöst werden können, sind:
- Angesichts der Kundendaten, Wie groß ist die Wahrscheinlichkeit, dass der Kunde ein neues Produkt kauft, das von einem Unternehmen präsentiert wird??
- Angesichts der erforderlichen Daten, Wie groß ist die Wahrscheinlichkeit, dass ein Bankkunde mit einem Kredit ausfällt??
- Angesichts der meteorologischen Daten des letzten Monats, Wie hoch ist die Wahrscheinlichkeit, dass es morgen regnet?
Alle obigen Aussagen hatten zwei Ergebnisse. (kaufen und nicht kaufen, Standard und Nicht-Standard, Regen und nicht Regen). Deswegen, ein binäres logistisches Regressionsmodell kann konstruiert werden. Die logistische Regression ist eine parametrische Methode. Was bedeutet das? Eine parametrische Methode hat zwei Schritte.
1. Zuerst, wir nehmen eine funktionale Form oder Form an. Im Falle einer logistischen Regression, Wir nehmen an, dass

2. Wir müssen die Gewichte vorhersagen / Koeffizienten bi so dass, die Wahrscheinlichkeit eines Ereignisses für eine Beobachtung x liegt nahe bei 1 wenn der tatsächliche Wert des Ziels 1 und die Wahrscheinlichkeit liegt nahe bei 0 wenn der tatsächliche Wert des Ziels 0.
Mit diesem Grundverständnis, Lassen Sie uns verstehen, warum wir eine Funktionsauswahl benötigen.
2. Bedeutung der Funktionsauswahl
In diesem digitalen Zeitalter, wir sind mit einer riesigen menge an daten ausgestattet. Aber trotzdem, nicht alle uns zur Verfügung stehenden Funktionen sind bei allen Modellvorhersagen sinnvoll. Wir alle kennen das Sprichwort „Trash in!, Müll kommt raus!”. Deswegen, Die Auswahl der richtigen Funktionen für unser Modell ist von größter Bedeutung. Features werden basierend auf der Vorhersagekraft des Features ausgewählt.
Zum Beispiel, Nehmen wir an, wir möchten die Wahrscheinlichkeit vorhersagen, mit der eine Person ein neues Hühnchenrezept in unserem Restaurant kauft. Wenn wir eine Funktion haben: „Essensvorliebe“ mit Werten {Vegetarier, Nicht vegetarisch, Eggetarian}, Wir sind uns ziemlich sicher, dass diese Funktion die Leute, die diese neue Platte eher kaufen, von denen, die sie nie kaufen werden, klar trennen wird. . Deswegen, diese Eigenschaft hat eine hohe Vorhersagekraft.
Wir können die Vorhersagekraft eines Merkmals mit dem hier beschriebenen Konzept des Informationswerts quantifizieren.
3. Benötigt einen guten Imputer für kategoriale Funktionen
Die logistische Regression ist eine parametrische Methode, bei der wir eine lineare Gleichung berechnen müssen. Dies erfordert, dass alle Merkmale numerisch sind. Aber trotzdem, Wir haben möglicherweise kategoriale Merkmale in unseren Datensätzen, die nominal oder ordinal sind. Es gibt viele Imputationsmethoden wie die One-Hot-Codierung oder die einfache Zuweisung einer Zahl zu jeder Klasse von kategorialen Merkmalen. jede dieser Methoden hat ihre eigenen Vor- und Nachteile. Aber trotzdem, Ich werde hier nicht dasselbe diskutieren.
Im Falle einer logistischen Regression, wir können das WoE-Konzept verwenden (Beweiskraft) kategoriale Merkmale unterstellen.
4. Beweiskraft
Nach all dem Hintergrund zur Verfügung gestellt, Endlich sind wir beim Thema des Tages angekommen!
Die Formel zur Berechnung der Beweiskraft für jedes Merkmal ist gegeben durch
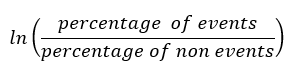
Bevor Sie die Intuition hinter dieser Formel erklären, nehmen wir ein fiktives beispiel:
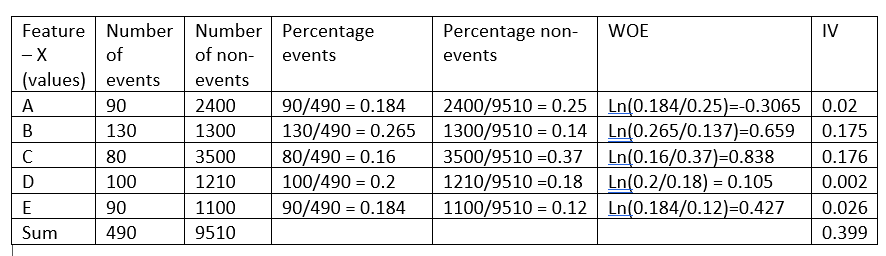
Die Beweiskraft gibt die Vorhersagekraft eines einzelnen Merkmals in Bezug auf sein unabhängiges Merkmal an.. Wenn eine der Kategorien / Bins eines Features haben einen großen Anteil an Ereignissen im Vergleich zu dem Anteil an keinen Ereignissen, Wir erhalten einen hohen WoE-Wert, der wiederum sagt, dass diese Art von Charakteristik die Ereignisse von den Nicht-Ereignissen trennt. .
Zum Beispiel, Betrachten Sie Kategorie C des Merkmals X im obigen Beispiel, der Anteil der Veranstaltungen (0,16) ist sehr klein im Vergleich zum Anteil der Nicht-Ereignisse (0,37). Dies impliziert, dass wenn der Wert des Merkmals X C . ist, der Zielwert ist eher 0 (kein Event). Der WoE-Wert sagt uns nur, wie sicher wir sind, dass die Funktion uns hilft, die Wahrscheinlichkeit eines Ereignisses richtig vorherzusagen.
Jetzt, da wir wissen, dass WoE die Vorhersagekraft jedes Bins misst / Kategorie einer Funktion, Was sind die anderen Vorteile von WoE?
1. Los valores de WoE para las diversas categorías de una VariableIn Statistik und Mathematik, ein "Variable" ist ein Symbol, das einen Wert darstellt, der sich ändern oder variieren kann. Es gibt verschiedene Arten von Variablen, und qualitativ, die nicht-numerische Eigenschaften beschreiben, und quantitative, numerische Größen darstellen. Variablen sind grundlegend in Experimenten und Studien, da sie die Analyse von Beziehungen und Mustern zwischen verschiedenen Elementen ermöglichen, das Verständnis komplexer Phänomene zu erleichtern.... categórica se pueden utilizar para imputar una característica categórica y convertirla en una característica numérica, da ein logistisches Regressionsmodell erfordert, dass alle seine Merkmale numerisch sind.
Durch sorgfältiges Untersuchen der WoE-Formel und der zu lösenden logistischen Regressionsgleichung, wir sehen, dass WoE eines Merkmals eine lineare Beziehung zu den logarithmischen Wahrscheinlichkeiten hat. Damit wird sichergestellt, dass die Forderung, dass die Kennlinien in einem linearen Zusammenhang mit den logarithmischen Wahrscheinlichkeiten stehen, erfüllt ist..
2. Aus dem gleichen Grund wie oben, wenn ein stetiges Feature keine lineare Beziehung zu den Log-Wahrscheinlichkeiten hat, Das Feature kann in Gruppen gruppiert und ein neues Feature erstellt werden, indem jeder Container durch seinen WoE-Wert anstelle des ursprünglichen Features ersetzt wird. Deswegen, WoE ist eine gute Methode zur Variablentransformation für die logistische Regression.
3. Durch Anordnen eines numerischen Merkmals in aufsteigender Reihenfolge, wenn die WoE-Werte alle linear sind, wir wissen, dass das Feature die korrekte lineare Beziehung zum Ziel hat. Aber trotzdem, wenn der WoE der Kennlinie nicht linear ist, wir müssen es verwerfen oder eine andere variable Transformation in Betracht ziehen, um die Linearität zu gewährleisten. Deswegen, WoE stellt uns ein Werkzeug zur Verfügung, um den linearen Zusammenhang mit der abhängigen Kennlinie zu verifizieren.
4. WoE ist besser als One-Hot-Encoding, da Sie beim One-Hot-Encoding neue h-1-Features erstellen müssen, um ein kategoriales Feature mit h-Kategorien unterzubringen. Dies impliziert, dass das Modell die Koeffizienten h-1 . nicht vorhersagen muss (mit einem) anstatt 1. Aber trotzdem, bei der Transformation der WoE-Variablen, wir müssen einen eindeutigen Koeffizienten für das betrachtete Merkmal berechnen.
5. Informationswert
Nachdem ich den WoE-Wert besprochen habe, der WoE-Wert sagt uns die Vorhersagekraft jedes Bins eines Merkmals. Aber trotzdem, ein einzelner Wert, der die Vorhersagekraft des gesamten Merkmals darstellt, ist bei der Merkmalsauswahl nützlich.
Die Gleichung für IV ist
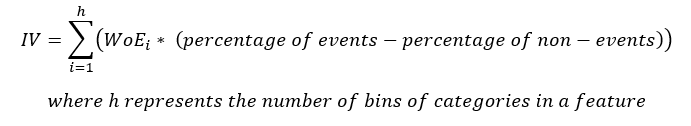
Beachten Sie, dass der Begriff (Prozentsatz der Ereignisse – der Prozentsatz ohne Ereignisse) folge dem gleichen Schild wie WoE, Daher, stellt sicher, dass die IV immer eine positive Zahl ist.
Wie interpretieren wir den Wert von IV?
Die folgende Tabelle enthält eine festgelegte Regel, die Ihnen bei der Auswahl der besten Funktionen für Ihr Modell hilft.
| Informationswert | Vorhersagekraft |
| <0.02 | Nutzlos |
| 0,02 bis um 0,1 | Schwache Prädiktoren |
| 0,1 bis um 0,3 | Mittlere Prädiktoren |
| 0,3 bis um 0,5 | Starke Prädiktoren |
| > 0,5 | Verdächtig |
Wie im obigen Beispiel zu sehen, Merkmal X hat einen Informationswert von 0.399, was es zu einem starken Prädiktor macht und, Daher, wird im Modell verwendet.
6. Fazit
Wie im obigen Beispiel zu sehen, Die Berechnung von WoE und IV ist von Vorteil und hilft uns, mehrere Punkte wie unten aufgeführt zu analysieren.
1. WoE hilft, die lineare Beziehung eines Features mit seinem im Modell zu verwendenden abhängigen Feature zu überprüfen.
2. WoE ist eine gute Methode zur Transformation von Variablen für kontinuierliche und kategoriale Merkmale.
3. WoE ist besser als Hot Encoding, da diese Methode der Variablentransformation die Komplexität des Modells nicht erhöht.
4. IV es una buena messenDas "messen" Es ist ein grundlegendes Konzept in verschiedenen Disziplinen, , die sich auf den Prozess der Quantifizierung von Eigenschaften oder Größen von Objekten bezieht, Phänomene oder Situationen. In Mathematik, Wird verwendet, um Längen zu bestimmen, Flächen und Volumina, In den Sozialwissenschaften kann es sich auf die Bewertung qualitativer und quantitativer Variablen beziehen. Die Messgenauigkeit ist entscheidend, um zuverlässige und valide Ergebnisse in der Forschung oder praktischen Anwendung zu erhalten.... del poder predictivo de una característica y también ayuda a señalar la característica sospechosa.
WoE und IV sind zwar sehr nützlich, Stellen Sie immer sicher, dass es nur mit logistischer Regression verwendet wird. Im Gegensatz zu anderen verfügbaren Methoden zur Funktionsauswahl, Die von IV ausgewählten Features sind möglicherweise nicht der beste Feature-Satz für eine nichtlineare Modellkonstruktion.
Ich hoffe, dieser Artikel hat Ihnen geholfen, die Bedienung von WoE und IV zu verstehen.
Die in diesem Artikel gezeigten Medien sind nicht Eigentum von DataPeaker und werden nach Ermessen des Autors verwendet.






