Dieser Artikel wurde im Rahmen der Data Science Blogathon.
Einführung
Eine beliebte und weit verbreitete statistische Methode zur Zeitreihenprognose ist das ARIMA-Modell.. Exponentielle Glättung und ARIMA-Modelle sind die beiden am häufigsten verwendeten Ansätze zur Vorhersage von Zeitreihen und bieten komplementäre Ansätze für das Problem.. Während exponentielle Glättungsmodelle auf einer Beschreibung des Trends und der Saisonalität der Daten basieren, ARIMA-Modelle zielen darauf ab, Autokorrelationen in den Daten zu beschreiben.
Um die Saisonalität zu kennen, Überprüfen Sie diesen Blog.
Bevor wir über das ARIMA-Modell sprechen, Sprechen wir über das Konzept der Stationarität und die Technik der Differenzierung von Zeitreihen.
Stationarität
Stationäre Zeitreihendaten sind Daten, deren Eigenschaften nicht von der Zeit abhängen, daher die Zeitreihen mit Trends, oder mit Saisonalität, sie sind nicht stationär. Trend und Saisonalität wirken sich zu unterschiedlichen Zeiten auf den Zeitreihenwert aus. Zweitens, für stationarität ist es egal, wenn man es betrachtet, sollte jederzeit sehr ähnlich aussehen. Allgemein, eine stationäre Zeitreihe wird keine vorhersagbaren langfristigen Muster aufweisen.
ARIMA ist ein Akronym für Auto-Regressive Integrated Moving Average. Es handelt sich um eine Modellklasse, die eine Reihe unterschiedlicher zeitlicher Standardstrukturen in Zeitreihendaten erfasst.
In diesem Tutorial, Wir werden darüber sprechen, wie man ein ARIMA-Modell für die Zeitreihenprognose in Python entwickelt.
Ein ARIMA-Modell ist eine Klasse statistischer Modelle zur Analyse und Vorhersage von Zeitreihendaten. Es ist wirklich vereinfacht in seiner Verwendung. Aber trotzdem, dieses modell ist wirklich mächtig.
ARIMA steht für Auto-Regressive Integrated Moving Average.
Die Parameter des ARIMA-Modells sind wie folgt definiert:
P: Die Anzahl der im Modell enthaltenen Lag-Beobachtungen, auch Verzögerungsreihenfolge genannt.
D: Wie oft sich Rohbeobachtungen unterscheiden, auch Differenzgrad genannt.
Q: Die Größe des gleitenden Durchschnittsfensters, auch gleitende Durchschnittsordnung genannt.
Es wird ein lineares Regressionsmodell erstellt, das die angegebene Anzahl und Art von Termen enthält, und die Daten werden durch ein gewisses Maß an Differenzierung aufbereitet, um sie stationär zu machen, nämlich, Beseitigung von Trend- und Saisonstrukturen, die sich negativ auf das Regressionsmodell auswirken.
SCHRITTE
1. Anzeigen von Zeitreihendaten
2. Feststellen, ob das Datum stationär ist
3. Zeichnen der Korrelations- und automatischen Korrelationsdiagramme
4. Erstellen Sie das ARIMA- oder saisonale ARIMA-Modell basierend auf den Daten
Lasst uns beginnen
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
In diesem Tutorial, Ich verwende den folgenden Datensatz.
df=pd.read_csv("time_series_data.csv")
df.kopf()
# Updating the header
df.columns=["Monat","Der Umsatz"]
df.kopf()
df.describe()
df.set_index('Monat',inplace=Wahr)
aus pylab importieren rcParams
rcParams['figur.feigengröße'] = 15, 7
df.plot()
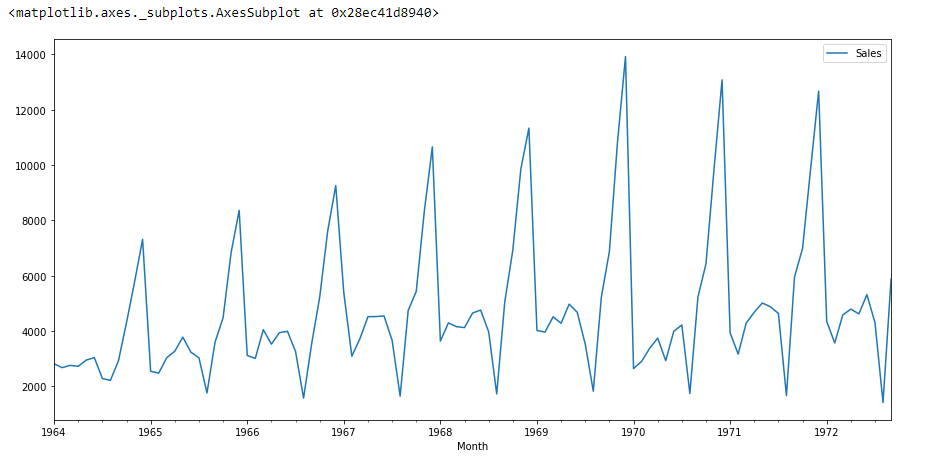
Wenn wir uns die obige Grafik ansehen, können wir einen Trend finden, dass es eine Zeit gibt, in der die Verkäufe hoch sind und umgekehrt. Das bedeutet, dass wir sehen können, dass die Daten der Saisonalität folgen.. Für ARIMA, Als erstes ermitteln wir, ob die Daten stationär oder nicht stationär sind. wenn die Daten nicht stationär sind, Wir werden versuchen, sie stationär zu machen und dann mehr zu verarbeiten.
Lassen Sie uns überprüfen, ob der gegebene Datensatz stationär ist oder nicht, dafür verwenden wir adfuller.
von statsmodels.tsa.stattools import adfuller
Ich habe den Adfuller importiert, indem ich den obigen Code ausgeführt habe.
test_result=adfuller(df['Der Umsatz'])
Um die Art der Daten zu identifizieren, wir verwenden die Nullhypothese.
H0: Die Nullhypothese: Es ist eine Aussage über die Bevölkerung, die für wahr gehalten wird oder zur Argumentation verwendet wird, es sei denn, sie kann zweifelsfrei als falsch nachgewiesen werden.
H1: Die Alternativhypothese: Es ist eine Aussage über die Bevölkerung, die widersprüchlich ist h0 und was wir schließen, wenn wir ablehnen h0.
#Ho: es ist nicht stationär
# H1: ist gestoppt
Wir betrachten die Nullhypothese, dass die Daten nicht stationär sind und die Alternativhypothese, dass die Daten stationär sind.
def adfuller_test(Der Umsatz):
result=adfuller(Der Umsatz)
Etiketten = ['ADF-Teststatistik','p-Wert','#Verzögerungen verwendet','Anzahl der Beobachtungen']
für Wert,Etikett im Reißverschluss(Ergebnis,Etiketten):
drucken(label+' : '+str(Wert) )
wenn ergebnis[1] <= 0.05:
drucken("Starke Beweise gegen die Nullhypothese(Ho), Ablehnen der Nullhypothese. Daten sind stationär")
anders:
drucken("schwache Evidenz gegen Nullhypothese,zeigt an, dass es nicht stationär ist ")
adfuller_test(df['Der Umsatz'])
Nachdem wir den obigen Code ausgeführt haben, erhalten wir den Wert P,
ADF-Teststatistik : -1.8335930563276237 p-Wert : 0.3639157716602447 #Verwendete Lags : 11 Anzahl der Beobachtungen : 93
Hier ist der Wert P 0.36, was größer ist als 0.05, was bedeutet, dass die Daten die Nullhypothese akzeptieren., was bedeutet, dass die Daten nicht stationär sind.
Versuchen wir, den ersten Unterschied und den saisonalen Unterschied zu sehen:
df["Umsatz erste Differenz"] = df['Der Umsatz'] - df['Der Umsatz'].Schicht(1) df["Saisonale erste Differenz"]=df['Der Umsatz']-df['Der Umsatz'].Schicht(12) df.kopf()

# Again testing if data is stationary
adfuller_test(df["Saisonale erste Differenz"].Tropfen())
ADF-Teststatistik : -7.626619157213163
p-Wert : 2.060579696813685e-11
#Lags Used : 0
Anzahl der Beobachtungen : 92
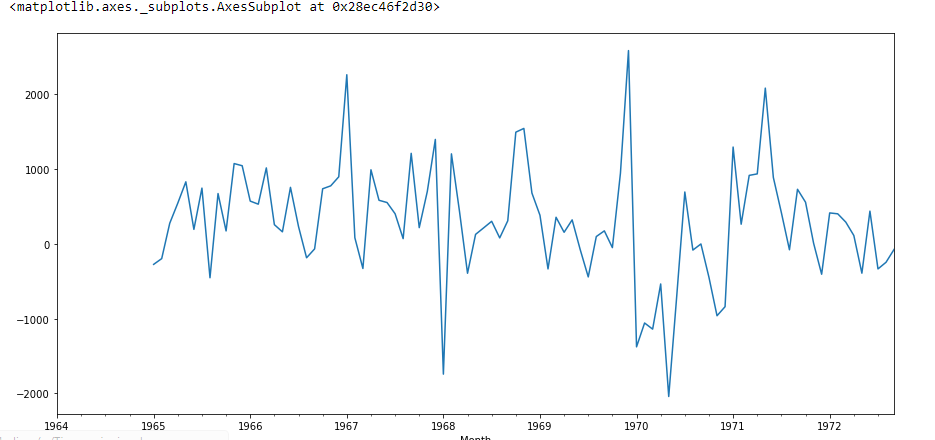
Hier ist der Wert P 2.06, was bedeutet, dass wir die Nullhypothese ablehnen werden. Dann sind die Daten stationär.
df["Saisonale erste Differenz"].Handlung()
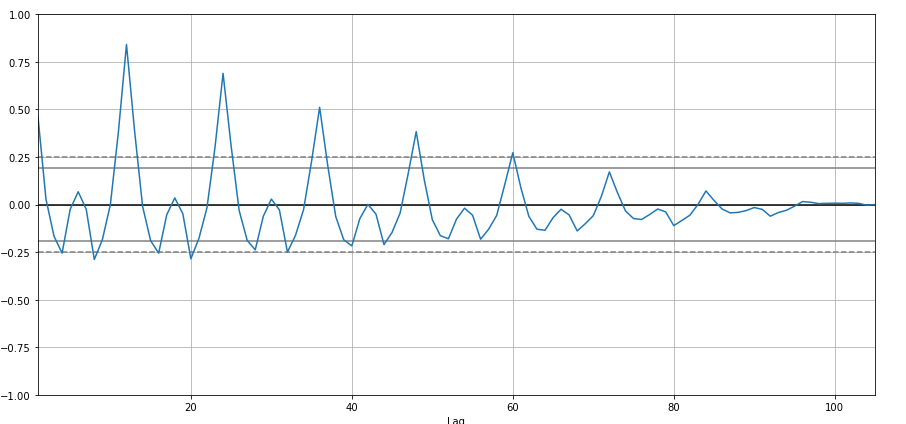
Ich werde Autokorrelation erstellen:
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(df['Der Umsatz'])
plt.zeigen()
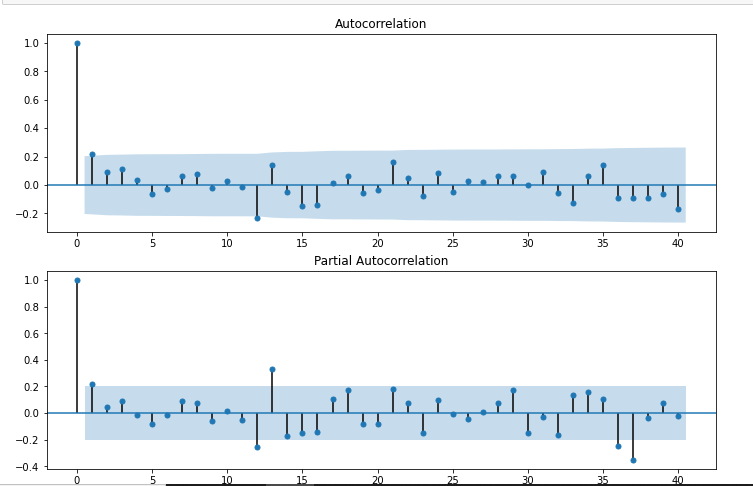
Aus statsmodels.graphics.tsaplots importieren Sie plot_acf,plot_pacf
import statsmodels.api as sm
fig = plt.figure(Feigengröße=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df["Saisonale erste Differenz"].Tropfen(),lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
Feige = sm.graphics.tsa.plot_pacf(df["Saisonale erste Differenz"].Tropfen(),lags=40,ax=ax2)
# For non-seasonal data #p=1, d=1, q=0 oder 1 from statsmodels.tsa.arima_model import ARIMA model=ARIMA(df['Der Umsatz'],bestellen=(1,1,1)) model_fit=Modell_Fit() model_fit.Zusammenfassung()
| Dep. Variable: | D. Der Umsatz | Nein. Beobachtungen: | 104 |
|---|---|---|---|
| Modell: | ARIMA (1, 1, 1) | Logarithmische Wahrscheinlichkeit | -951.126 |
| Methode: | css-mle | SD de innovaciones | 2227.262 |
| Datum: | Mié |, 28 Okt 2020 | AIC | 1910.251 |
| Wetter: | 11:49:08 | BIC | 1920.829 |
| Zeigt an: | 02-01-1964 | HQIC | 1914.536 |
| – 09-01-1972 |
| coef | std err | Mit | P> | Mit | | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Konstante | 22.7845 | 12.405 | 1.837 | 0.066 | -1.529 | 47.098 |
| Ar. L1. D.Vertrieb | 0.4343 | 0,089 | 4.866 | 0.000 | 0,259 | 0,609 |
| Mutti. L1. D.Vertrieb | -1,0000 | 0,026 | -38.503 | 0.000 | -1.051 | -0,949 |
| Wahr | Imaginario | Modul | Frequenz | |
|---|---|---|---|---|
| AR.1 | 2.3023 | + 0,0000J | 2.3023 | 0,0000 |
| MA.1 | 1,0000 | + 0,0000J | 1,0000 | 0,0000 |
df["Prognose"]=model_fit.predict(start=90;end=103,dynamic=True) df[['Der Umsatz',"Prognose"]].Handlung(Feigengröße=(12,8))
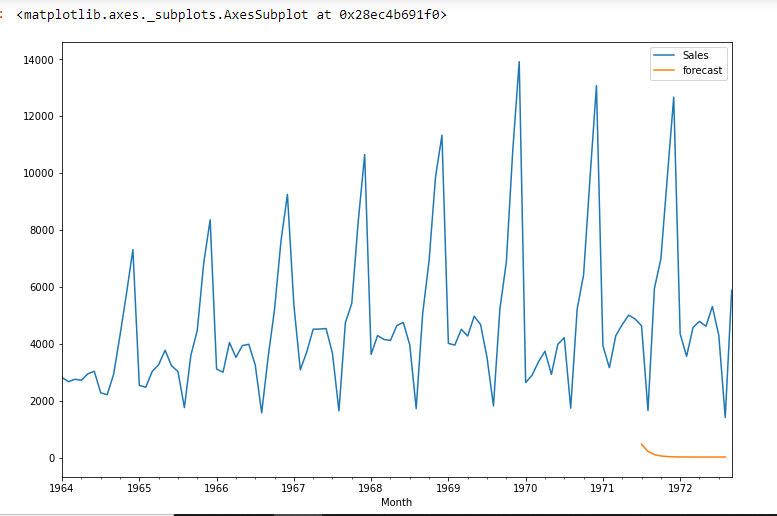
import statsmodels.api as sm
model=sm.tsa.statespace.SARIMAX(df['Der Umsatz'],bestellen=(1, 1, 1),seasonal_order=(1,1,1,12))
Ergebnisse=Modell.Fit()
df["Prognose"]=Ergebnisse.Vorhersage(start=90;end=103,dynamic=True)
df[['Der Umsatz',"Prognose"]].Handlung(Feigengröße=(12,8))
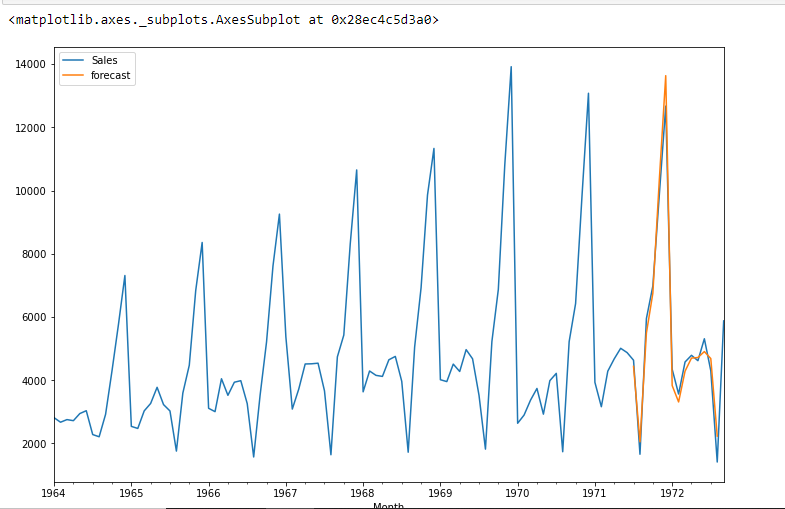
from pandas.tseries.offsets import DateOffset
future_dates=[df.index[-1]+ DateOffset(Monate=x)für x im Bereich(0,24)]
future_datest_df=pd. DataFrame(index=future_dates[1:],Spalten=df.Spalten)
future_datest_df.Schwanz()
future_df=pd.concat([df,future_datest_df])
future_df["Prognose"] = Ergebnisse.vorhersagen(beginnen = 104, Ende = 120, dynamisch = wahr)
future_df[['Der Umsatz', "Prognose"]].Handlung(Feigengröße=(12, 8))
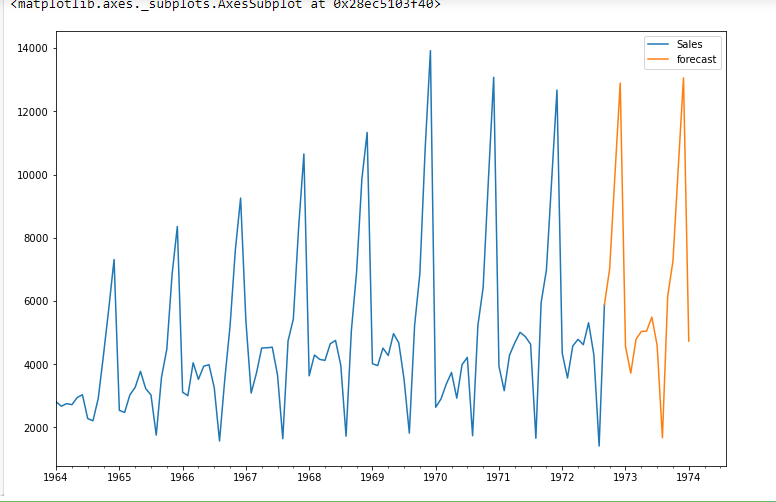
Fazit
Zeitreihenprognosen sind sehr nützlich, wenn wir zukünftige Entscheidungen treffen oder Analysen durchführen müssen, Wir können es schnell mit ARIMA . machen, Es gibt viele andere Modelle, mit denen wir Zeitreihenprognosen durchführen können, aber ARIMA ist wirklich leicht zu verstehen.
Ich hoffe, dieser Artikel hilft Ihnen und spart Ihnen viel Zeit. Lassen Sie es mich wissen, wenn Sie Vorschläge haben..
GLÜCKLICHES CODIEREN.
Prabhat Pathak (LinkedIn Profil) ist ein leitender Analyst.






