Qu'est-ce que l'apprentissage en profondeur? Tutoriel d'apprentissage en profondeur

Cet article a été publié dans le cadre du Blogathon sur la science des données.

Le guide est principalement pour les débutants, et j'essaierai de définir et de souligner les thèmes autant que possible. Dado que el l'apprentissage en profondeurL'apprentissage en profondeur, Une sous-discipline de l’intelligence artificielle, s’appuie sur des réseaux de neurones artificiels pour analyser et traiter de grands volumes de données. Cette technique permet aux machines d’apprendre des motifs et d’effectuer des tâches complexes, comme la reconnaissance vocale et la vision par ordinateur. Sa capacité à s’améliorer continuellement au fur et à mesure que de nouvelles données lui sont fournies en fait un outil clé dans diverses industries, de la santé... es un tema muy grande, Je diviserais tout le tutoriel en quelques parties. Assurez-vous de lire les autres parties si vous trouvez cela utile.

Contenu

1. introduction

• Qu'est-ce que l'apprentissage en profondeur?
• Pourquoi l'apprentissage en profondeur?
• Combien de données sont volumineuses?
• Domaines où le deep learning est utilisé
• Diferencia entre Deep Learning et Machine Learning

2) Importez les bibliothèques requises

3) résumé

4) Régression logistique

• Graphe de calcul
• Inicializando paramètresLes "paramètres" sont des variables ou des critères qui sont utilisés pour définir, mesurer ou évaluer un phénomène ou un système. Dans divers domaines tels que les statistiques, Informatique et recherche scientifique, Les paramètres sont essentiels à l’établissement de normes et de standards qui guident l’analyse et l’interprétation des données. Leur sélection et leur manipulation correctes sont cruciales pour obtenir des résultats précis et pertinents dans toute étude ou projet....
• Propagation vers l'avant
• Optimisation avec Gradient Descent

5) Régression logistique avec Sklearn

6) Remarques finales

introduction

Qu'est-ce que l'apprentissage en profondeur?

• C'est un sous-domaine de l'apprentissage automatique, inspiré par les neurones biologiques du cerveau et le traduisant en réseaux de neurones artificiels avec apprentissage de la représentation.

Pourquoi l'apprentissage en profondeur?

• Lorsque le volume de données augmente, techniques d'apprentissage automatique, peu importe à quel point ils sont optimisés, commencent à devenir inefficaces en termes de performances et de précision, tandis que l'apprentissage en profondeur fonctionne beaucoup mieux dans de tels cas.

Combien de données sont volumineuses?

• Bon, un seuil ne peut pas être quantifié pour que les données soient considérées comme grandes, mais, intuitivement, Disons qu'un échantillon d'un million pourrait suffire à dire “C'est grand” (c'est là que Michael Scott aurait prononcé ses fameuses paroles “C'est ce qu'elle a dit”).

Champs où DL est utilisé

• Classification des images, reconnaissance vocale, PNL (traitement du langage naturel), systèmes de recommandation, etc.

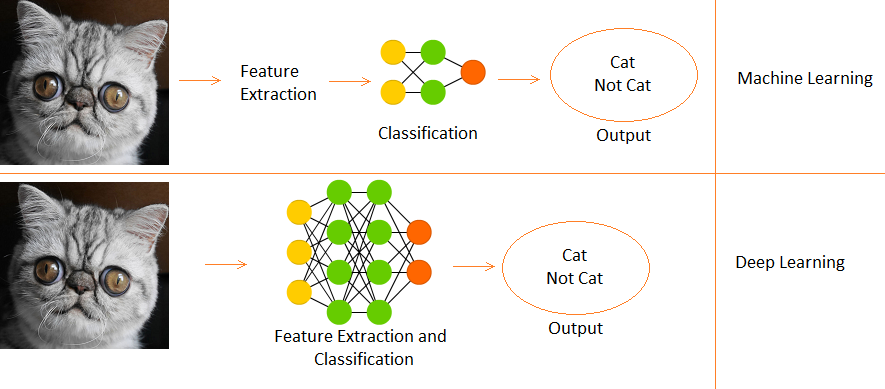
Différence entre l'apprentissage en profondeur et l'apprentissage automatique

• L'apprentissage profond est un sous-ensemble de l'apprentissage automatique.
• Fr Apprentissage automatique, les fonctions sont fournies manuellement.
• Tandis que Deep Learning apprend les fonctions directement à partir des données.

Nous utiliserons le Ensemble de données de chiffres en langue des signes qui est disponible sur Kaggle ici. Commençons maintenant.

Importer les bibliothèques requises

importer numpy en tant que np # algèbre linéaire
importer des pandas au format pd # traitement de l'information, E/S de fichier CSV (par exemple. pd.read_csv)
importer matplotlib.pyplot en tant que plt
# Les fichiers de données d'entrée sont disponibles dans le "../saisir/" annuaire.
# avertissements d'importation
avertissements d'importation
# avertissements de filtre
warnings.filterwarnings('ignorer')
à partir du sous-processus import check_output
imprimer(check_output(["ls", "../saisir"]).décoder("utf8"))
# Tous les résultats que vous écrivez dans le répertoire actuel sont enregistrés en tant que sortie.

Résumé des données

• Il y a 2062 images de chiffres en langue des signes dans cet ensemble de données.
• Puisqu'il y a 10 chiffres de 0 Al 9, il y a 10 images de signaux uniques.
• Au début, nous n'utiliserons que 0 Oui 1 (pour faire simple pour les étudiants)
• Dans les données, le signe de la main pour 0 est entre les index 204 Oui 408. Il y a 205 échantillons pour 0.
• En outre, le signe de la main pour 1 est entre les index 822 Oui 1027. Il y a 206 échantillons.
• Donc, nous utiliserons 205 échantillons de chaque classe (Noter: en réalité, 205 les échantillons sont beaucoup moins pour un modèle d'apprentissage en profondeur approprié, mais comme c'est un tuto, on peut l'ignorer),

Nous allons maintenant préparer nos matrices X et Y, où X est notre matrice image (fonctionnalités) et Y est notre matrice d'étiquettes (0 Oui 1).

# charger l'ensemble de données
x_l = np.charge('../input/Sign-language-digits-dataset/X.npy')
Y_l = np.charge('../input/Sign-language-digits-dataset/Y.npy')
img_size = 64
plt.sous-intrigue(1, 2, 1)
plt.imshow(x_l[260].remodeler(img_size, img_size))
plt.axis('désactivé')
plt.sous-intrigue(1, 2, 2)
plt.imshow(x_l[900].remodeler(img_size, img_size))
plt.axis('désactivé')

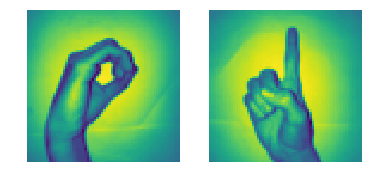
# Joindre une séquence de tableaux le long d'un axe de ligne.
# de 0 à 204 est de signe zéro et de 205 à 410 est un signe
X = np.concaténer((x_l[204:409], x_l[822:1027] ), axe=0)
z = np.zéros(205)
o = np.uns(205)
Y = np.concaténer((Avec, O), axe=0).remodeler(X.forme[0],1)
imprimer("forme X: " , X.forme)
imprimer("forme de Y: " , Y.forme)

Pour créer notre matrice X, Nous avons d'abord divisé et concaténé nos segments d'images de signes de main à partir de 0 Oui 1 de l'ensemble de données à la matrice X. Ensuite, nous faisons quelque chose de similaire avec Y, mais nous utilisons les balises à la place.

1) On voit donc que la forme de notre matrice X est (410, 64, 64)

• Le 410 ça veut dire 205 images de 0, 205 images de 1.
• les 64 signifie que la taille de nos images est 64 X 64 pixels.

2) La forme en Y est (410,1), donc, 410 des uns et des zéros.

3) Maintenant, nous divisons X et Y en trains et ensembles de test.

• train = 75%, train = 15%
• random_state = Utiliser une graine particulière lors de la randomisation, donc, si la cellule s'exécute plusieurs fois, le nombre aléatoire généré ne change pas à chaque fois. La même disposition de test et de train est créée à chaque fois.

# Ensuite, créons x_train, y_train, x_test, y_test tableaux
de sklearn.model_selection importer train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Oui, taille_test=0.15, état_aléatoire=42)
number_of_train = X_train.shape[0]
nombre_de_test = X_test.shape[0]

Nous avons une matrice d'entrée tridimensionnelle, nous devons donc l'aplatir en 2D pour alimenter notre premier modèle d'apprentissage en profondeur. Comme et est déjà 2D, on le laisse tel quel.

X_train_flatten = X_train.reshape(nombre_de_train,X_train.shape[1]*X_train.shape[2])
X_test_flatten = X_test .reshape(nombre_de_tests,X_test.shape[1]*X_test.shape[2])
imprimer("X train aplatir",X_train_flatten.shape)
imprimer("Test X aplatir",X_test_flatten.shape)

Nous avons maintenant un total de 348 images, chacun avec 4096 píxeles en la matriz de entraînementLa formation est un processus systématique conçu pour améliorer les compétences, connaissances ou aptitudes physiques. Il est appliqué dans divers domaines, Comme le sport, Éducation et développement professionnel. Un programme d’entraînement efficace comprend la planification des objectifs, Pratique régulière et évaluation des progrès. L’adaptation aux besoins individuels et la motivation sont des facteurs clés pour obtenir des résultats réussis et durables dans toutes les disciplines.... X. Oui 62 images de même densité de pixels 4096 dans la matrice de test. On transpose maintenant les matrices. Ceci est juste un choix personnel et vous verrez dans les prochains codes pourquoi je le dis.

x_train = X_train_flatten.T
x_test = X_test_flatten.T
y_train = Y_train.T
y_test = Y_test.T
imprimer("x_train: ",x_train.shape)
imprimer("x_test: ",x_test.shape)
imprimer("y_train: ",y_train.shape)
imprimer("y_test: ",y_test.shape)

Alors maintenant, nous avons terminé de préparer nos données requises. Voilà à quoi ça ressemble:

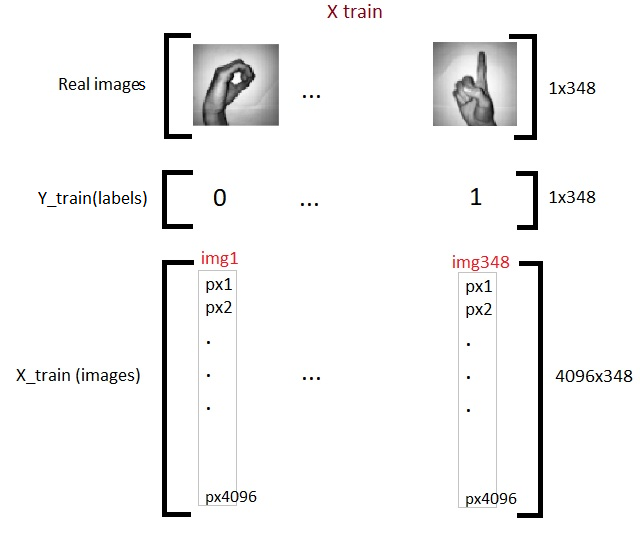
Nous allons maintenant nous familiariser avec l'un des modèles de base de Dl, appelée régression logistique.

Régression logistique

Quand on parle de classification binaire, le premier modèle qui me vient à l'esprit est la régression logistique. Mais on peut se demander à quoi sert la régression logistique dans le deep learning ?? La réponse est simple, ya que la regresión logística es una neuronal rougeLes réseaux de neurones sont des modèles computationnels inspirés du fonctionnement du cerveau humain. Ils utilisent des structures appelées neurones artificiels pour traiter et apprendre des données. Ces réseaux sont fondamentaux dans le domaine de l’intelligence artificielle, permettant des avancées significatives dans des tâches telles que la reconnaissance d’images, Traitement du langage naturel et prédiction de séries temporelles, entre autres. Leur capacité à apprendre des motifs complexes en fait des outils puissants.. Facile. Les termes réseau de neurones et apprentissage en profondeur vont de pair. Comprendre la régression logistique, nous devons d'abord apprendre l'infographie.

Tableau de calcul

L'infographie peut être considérée comme une manière imagée de représenter des expressions mathématiques. Comprenons qu'avec un exemple. Supposons que nous ayons une expression mathématique simple comme:

c = ( une² + b² ) ^1/2

Votre graphique de calcul sera:

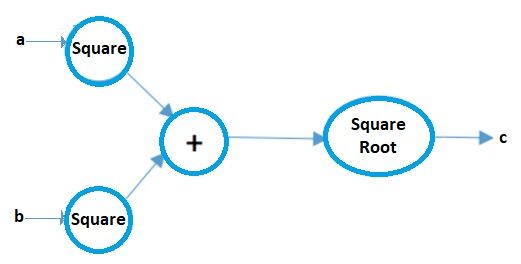
Source de l'image: Auteur

Regardons maintenant un graphique de calcul de régression logistique:

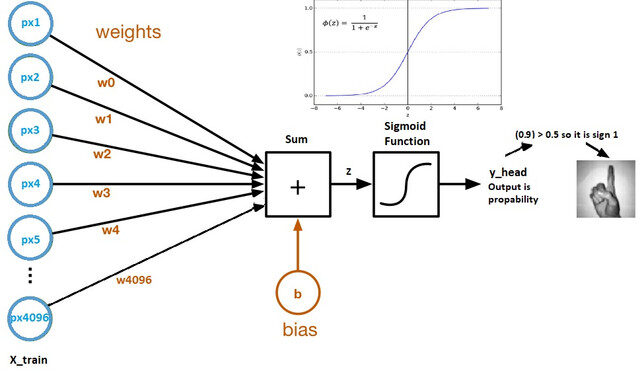
Source de l'image: Ensemble de données Kaggle

• Les poids et les biais sont appelés paramètres du modèle.
• Les poids représentent les coefficients de chaque pixel.
• L'asymétrie est l'intersection de la courbe formée en traçant les paramètres par rapport aux étiquettes.
• Z = (px1 * wx1) + (px2 * wx2) +…. + (px4096 * wx4096)
• y_head = sigmoid_funtion (AVEC)
• Ce que fait la fonction sigmoïde, c'est essentiellement mettre à l'échelle la valeur de Z entre 0 Oui 1, donc ça devient une probabilité.

Pourquoi utiliser la fonction sigmoïde?

• Cela nous donne un résultat probabiliste.
• Comme il s'agit d'un dérivé, podemos usarlo en el algoritmo de descenso de penteLe gradient est un terme utilisé dans divers domaines, comme les mathématiques et l’informatique, pour décrire une variation continue de valeurs. En mathématiques, fait référence au taux de variation d’une fonction, pendant la conception graphique, S’applique à la transition de couleur. Ce concept est essentiel pour comprendre des phénomènes tels que l’optimisation dans les algorithmes et la représentation visuelle des données, permettant une meilleure interprétation et analyse dans....

Nous allons maintenant examiner en détail chacune des composantes du graphe de calcul ci-dessus.

Paramètres d'initialisation

Source de l'image: Documents Microsoft

Chaque pixel a son propre poids. Mais la question est de savoir quels seront vos poids initiaux? Il existe plusieurs techniques pour faire cela que je couvrirai dans la partie 2 de cet article, Mais pour l'instant, nous pouvons les initialiser en utilisant n'importe quelle valeur aléatoire, Disons 0.01.

La forme de la matrice de poids sera (4096, 1), puisqu'il y a un total de 4096 pixels par image, et que le biais initial soit 0.

# permet d'initialiser les paramètres
# Donc ce dont nous avons besoin, c'est de la dimension 4096 c'est le nombre de pixels en tant que paramètre pour notre méthode d'initialisation(déf)
def initialize_weights_and_bias(dimension):
    w = np.plein((dimension,1),0.01)
    b = 0.0
    retour w, b

w,b = initialize_weights_and_bias(4096)

Propagation vers l'avant

Toutes les étapes des pixels à la fonction de coût sont appelées propagation vers l'avant.

Pour calculer Z, nous utilisons la formule: Z = (poids) X + b. où x est la matrice de pixels, w poids et b est le biais. Après avoir calculé Z, nous l'introduisons dans la fonction sigmoïde qui renvoie y_head (probabilité). Après cela, calculamos la Fonction de perteLa fonction de perte est un outil fondamental de l’apprentissage automatique qui quantifie l’écart entre les prédictions du modèle et les valeurs réelles. Son but est de guider le processus de formation en minimisant cette différence, permettant ainsi au modèle d’apprendre plus efficacement. Il existe différents types de fonctions de perte, tels que l’erreur quadratique moyenne et l’entropie croisée, chacun adapté à différentes tâches et... (Erreur).

La fonction de coût est la somme de toutes les pertes et pénalise le modèle pour les prédictions incorrectes. C'est ainsi que notre modèle apprend les paramètres.

# calcul de z
#z = np.dot(avec T,x_train)+b
def sigmoïde(Avec):
    y_head = 1/(1+np.exp(-Avec))
    retourner y_head

y_head = sigmoïde(0)
y_head
> 0.5

L'expression mathématique de la fonction de perte (Journal) il est:

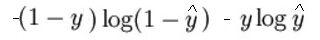
Comme je l'ai dit plus tôt, ce que fait essentiellement la fonction de perte, c'est de pénaliser les prédictions incorrectes. voici le code pour la propagation vers l'avant:

# Étapes de propagation vers l'avant:
# trouver z = w.T*x+b
# y_head = sigmoïde(Avec)
# perte(Erreur) = perte(Oui,y_head)
# coût = somme(perte)
def propagation_avant(w,b,x_train,y_train):
    z = par exemple à(avec T,x_train) + b
    y_head = sigmoïde(Avec) # probabiliste 0-1
    perte = -y_train*np.log(y_head)-(1-y_train)*np.log(1-y_head)
    coût = (np.sum(perte))/x_train.shape[1]      # x_train.shape[1]  est pour la mise à l'échelle
    frais de retour

Optimisation avec Gradient Descent

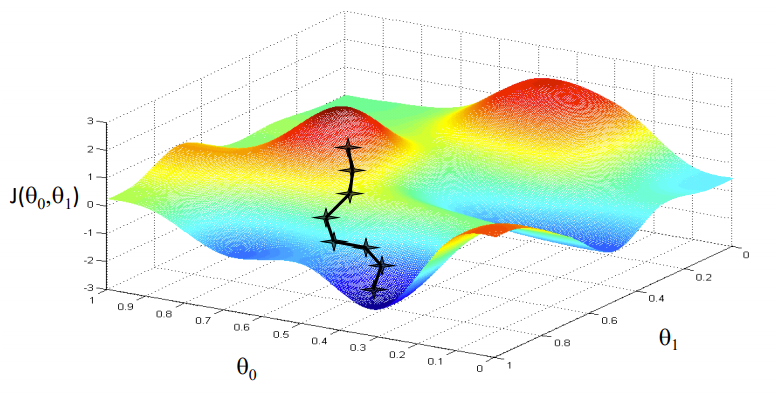
Source de l'image: Coursera

Notre objectif est de trouver les valeurs de nos paramètres pour lesquelles, la fonction de perte est le minimum. L'équation de la descente de pente est:

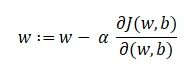
Où w est le poids ou le paramètre. La lettre grecque alpha est ce qu'on appelle la taille du pas. Cela signifie la taille des itérations que nous prendrons au fur et à mesure que nous descendons la pente pour trouver les minima locaux. Et le reste est la dérivée de la fonction de perte, également connu sous le nom de dégradé. L'algorithme de descente de gradient est simple:

1. Premier, nous prenons un point de données aléatoire sur notre graphique et trouvons sa pente.
2. Ensuite, nous trouvons la direction dans laquelle la fonction de perte diminue.
3. Mettre à jour les poids en utilisant la formule ci-dessus. (Cette méthode est également appelée rétropropagation.)
4. Sélectionnez le point suivant en prenant une taille de α.
5. Répéter.

# En propagation vers l'arrière, nous utiliserons y_head que l'on trouve dans la propagation vers l'avant
# Par conséquent, au lieu d'écrire la méthode de propagation en arrière, permet de combiner la propagation vers l'avant et la propagation vers l'arrière
def forward_backward_propagation(w,b,x_train,y_train):
    # propagation vers l'avant
    z = np.dot(avec T,x_train) + b
    y_head = sigmoïde(Avec)
    perte = -y_train*np.log(y_head)-(1-y_train)*np.log(1-y_head)
    coût = (np.sum(perte))/x_train.shape[1]      # x_train.shape[1]  est pour la mise à l'échelle
    # propagation vers l'arrière
    poids_dérivé = (np.dot(x_train,((y_head-y_train).T)))/x_train.shape[1] # x_train.shape[1]  est pour la mise à l'échelle
    dérivé_biais = np.sum(y_head-y_train)/x_train.shape[1]                 # x_train.shape[1]  est pour la mise à l'échelle
    dégradés = {"poids_dérivé": poids_dérivé,"biais_dérivé": biais_dérivé}
    frais de retour,dégradés

Maintenant, nous mettons à jour les paramètres d'apprentissage:

# Mise à jour(apprentissage) paramètres
mise à jour def(w, b, x_train, y_train, taux d'apprentissage,nombre_d'itérations):
    liste_coûts = []
    cost_list2 = []
    indice = []
    # mise à jour(apprentissage) paramètres est nombre_de_itérations fois
    pour moi à portée(nombre_d'itérations):
        # faire une propagation en avant et en arrière et trouver des coûts et des gradients
        Coût,gradients = forward_backward_propagation(w,b,x_train,y_train)
        cost_list.append(Coût)
        # permet de mettre à jour
        w = w - taux d'apprentissage * dégradés["poids_dérivé"]
        b = b - taux d'apprentissage * dégradés["biais_dérivé"]
        si je % 10 == 0:
            cost_list2.append(Coût)
            index.append(je)
            imprimer ("Coût après itération %i: %F" %(je, Coût))
    # nous mettons à jour(apprendre) poids des paramètres et biais
    paramètres = {"poids": w,"biais": b}
    plt.plot(indice,liste_coût2)
    plt.xticks(indice,rotation='vertical')
    plt.xlabel("Nombre d'itérations")
    plt.ylabel("Coût")
    plt.show()
    paramètres de retour, dégradés, liste_coûts

paramètres, dégradés, cost_list = mise à jour(w, b, x_train, y_train, taux d'apprentissage = 0,009, nombre_de_itérations = 200)

Jusque là, nous avons appris nos paramètres. Cela signifie que nous ajustons les données. Dans l'étape de prédiction, nous avons x_test en entrée et l'utilisons, nous faisons des prévisions.

 # prédiction
def prédire(w,b,x_test):
    # x_test est une entrée pour la propagation vers l'avant
    z = sigmoïde(np.dot(avec T,x_test)+b)
    Y_prediction = np.zéros((1,x_test.shape[1]))
    # si z est plus grand que 0.5, notre prédiction est le signe un (y_head=1),
    # si z est plus petit que 0.5, notre prédiction est signe zéro (y_head=0),
    pour moi à portée(z.forme[1]):
        si z[0,je]<= 0.5:
            Y_prédiction[0,je] = 0
        autre:
            Y_prédiction[0,je] = 1

    renvoyer Y_prediction

prédire(paramètres["poids"],paramètres["biais"],x_test)

Maintenant, nous faisons nos prédictions. Mettons le tout ensemble:

def régression_logistique(x_train, y_train, x_test, y_test, taux d'apprentissage ,  nombre_itérations):
    # initialiser
    dimension = x_train.forme[0]  # C'est 4096
    w,b = initialize_weights_and_bias(dimension)
    # ne pas changer le taux d'apprentissage
    paramètres, dégradés, cost_list = mise à jour(w, b, x_train, y_train, taux d'apprentissage,nombre_itérations)
    
    y_prediction_test = prédire(paramètres["poids"],paramètres["biais"],x_test)
    y_prediction_train = prédire(paramètres["poids"],paramètres["biais"],x_train)

    # Erreurs de train/test d'impression
    imprimer("précision des trains: {} %".format(100 - np.moyenne(np.abs(y_prediction_train - y_train)) * 100))
    imprimer("tester la précision: {} %".format(100 - np.moyenne(np.abs(y_prediction_test - y_test)) * 100))
    
régression logistique(x_train, y_train, x_test, y_test,taux_apprentissage = 0.01, nombre_itérations = 150)

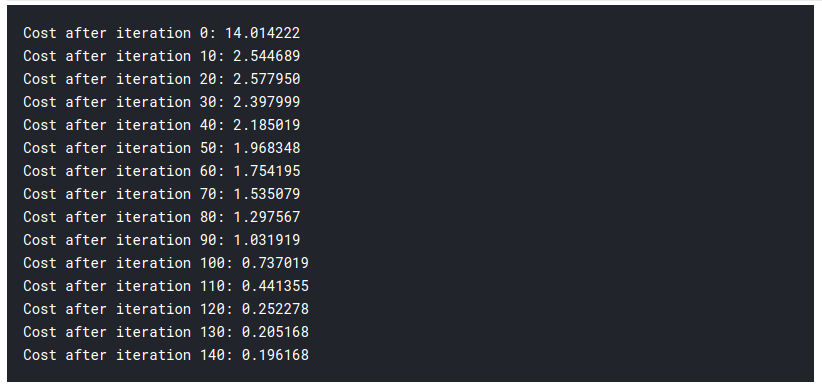
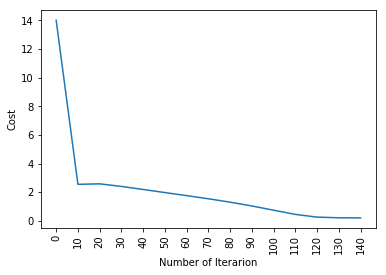
Ensuite, Comme vous pouvez le voir, même le modèle le plus fondamental d'apprentissage en profondeur est assez difficile. Ce n'est pas facile pour toi d'apprendre, et les débutants peuvent parfois se sentir dépassés par l'étude de tout cela à la fois. Mais le fait est que nous n'avons pas encore touché à l'apprentissage en profondeur., c'est comme la surface. Il y a beaucoup plus que je vais ajouter dans la partie 2 de cet article.

Puisque nous avons appris la logique derrière la régression logistique, nous pouvons utiliser une bibliothèque appelée SKlearn qui possède déjà de nombreux modèles et algorithmes intégrés, vous n'avez donc pas besoin de tout recommencer à zéro.

Régression logistique avec Sklearn

Je ne vais pas expliquer grand-chose dans cette section puisque vous connaissez presque toute la logique et l'intuition derrière la régression logistique.. Si vous souhaitez en savoir plus sur la bibliothèque Sklearn, vous pouvez lire la documentation officielle ici. Voici le code, et je suis sûr que tu seras stupéfait de voir à quel point il faut peu d'efforts:

de sklearn importer linear_model
logreg = linear_model.LogisticRegression(état_aléatoire = 42,iter_max= 150)
imprimer("tester la précision: {} ".format(logreg.fit(x_train.T, y_train.T).But(x_test.T, y_test.T)))
imprimer("précision des trains: {} ".format(logreg.fit(x_train.T, y_train.T).But(x_train.T, y_train.T)))

Oui! c'est tout ce qu'il a fallu, solo 1 ligne de code!

Remarques finales

Nous avons beaucoup appris aujourd'hui. Mais c'est seulement le début. Assurez-vous de vérifier la partie 2 de cet article. Vous pouvez le trouver dans le lien suivant. Si vous aimez ce que vous lisez, vous pouvez lire certains des autres articles intéressants que j'ai écrits.

Sion | Auteur chez DataPeaker

J'espère que vous avez passé un bon moment à lire mon article. Santé!!

Les médias présentés dans cet article sur les meilleures bibliothèques d'apprentissage automatique dans Julia ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.

En rapport