El árbol comienza con el nœudNodo est une plateforme digitale qui facilite la mise en relation entre les professionnels et les entreprises à la recherche de talents. Grâce à un système intuitif, Permet aux utilisateurs de créer des profils, Partager des expériences et accéder à des opportunités d’emploi. L’accent mis sur la collaboration et le réseautage fait de Nodo un outil précieux pour ceux qui souhaitent élargir leur réseau professionnel et trouver des projets qui correspondent à leurs compétences et à leurs objectifs.... raíz que consta de los datos completos y, ensuite, utiliser des stratégies intelligentes pour diviser les nœuds en plusieurs branches.
L'ensemble de données d'origine a été divisé en sous-ensembles dans ce processus.
Pour répondre à la question fondamentale, ton cerveau inconscient fait des calculs (à la lumière des exemples de questions enregistrés ci-dessous) et finit par acheter la quantité de lait nécessaire. Est-ce normal ou en semaine?
Les jours ouvrables, nous exigeons 1 litre de lait.
C'est un week-end? Le week-end, nous avons besoin 1,5 litres de lait.
Est-il exact de dire que nous attendons des invités aujourd'hui? Nous avons besoin d'acheter 250 ML de lait supplémentaire pour chaque invité, et ainsi de suite.
Avant de sauter à l'idée hypothétique des arbres de décision, Et si nous expliquions dans un premier temps quels sont les arbres de décision? C'est plus, Pourquoi serait-ce une bonne idée pour nous de les utiliser?
Pourquoi utiliser des arbres de décision?
Entre otros métodos de enseignement superviséL’apprentissage supervisé est une approche d’apprentissage automatique dans laquelle un modèle est formé à l’aide d’un ensemble de données étiquetées. Chaque entrée du jeu de données est associée à une sortie connue, permettre au modèle d’apprendre à prédire les résultats pour de nouvelles entrées. Cette méthode est largement utilisée dans des applications telles que la classification d’images, Reconnaissance vocale et prédiction de tendances, soulignant son importance dans..., les algorithmes arborescents excellent. Ce sont des modèles prédictifs avec une plus grande précision et une compréhension simple.
Comment fonctionne l'arbre de décision?
Il existe différents algorithmes écrits pour assembler un arbre de décision, qui peut être utilisé pour le problème.
Certains des algorithmes les plus couramment utilisés sont répertoriés ci-dessous:
• CHARIOT
• ID3
• C4.5
• CHAID
Nous allons maintenant expliquer l'algorithme CHAID étape par étape. Avant que, on va parler un peu de chi_square.
chi_carré
Chi-Cuadrado es una mesureLa "mesure" C’est un concept fondamental dans diverses disciplines, qui fait référence au processus de quantification des caractéristiques ou des grandeurs d’objets, phénomènes ou situations. En mathématiques, Utilisé pour déterminer les longueurs, Surfaces et volumes, tandis qu’en sciences sociales, il peut faire référence à l’évaluation de variables qualitatives et quantitatives. La précision des mesures est cruciale pour obtenir des résultats fiables et valides dans toute recherche ou application pratique.... estadística para encontrar la diferencia entre los nodos secundarios y principales. Pour calculer cela, encontramos la diferencia entre los conteos observados y esperados de la variableEn statistique et en mathématiques, ongle "variable" est un symbole qui représente une valeur qui peut changer ou varier. Il existe différents types de variables, et qualitatif, qui décrivent des caractéristiques non numériques, et quantitatif, représentation de grandeurs numériques. Les variables sont fondamentales dans les expériences et les études, puisqu’ils permettent l’analyse des relations et des modèles entre différents éléments, faciliter la compréhension de phénomènes complexes.... objetivo para cada nodo y la suma al cuadrado de estas diferencias estandarizadas nos dará el valor de Chi-cuadrado.
Formule
Pour trouver la caractéristique la plus dominante, les tests du chi carré utiliseront ce qui est aussi appelé CHAID, tandis que ID3 utilise le gain d'informations, C4.5 usa la relación de ganancia y CART usa el indiceLe "Indice" C’est un outil fondamental dans les livres et les documents, qui vous permet de localiser rapidement les informations souhaitées. Généralement, Il est présenté au début d’une œuvre et organise les contenus de manière hiérarchique, y compris les chapitres et les sections. Sa préparation correcte facilite la navigation et améliore la compréhension du matériau, ce qui en fait une ressource incontournable tant pour les étudiants que pour les professionnels dans divers domaines.... GINI.
Aujourd'hui, la plupart des bibliothèques de programmation (par exemple, Pandas pour Python) utiliser la métrique de Pearson pour la corrélation par défaut.
La formule du chi carré: –
√ ((Oui – Oui ‘)2 / Oui ‘)
donde y es real y se espera y ‘.
Base de données
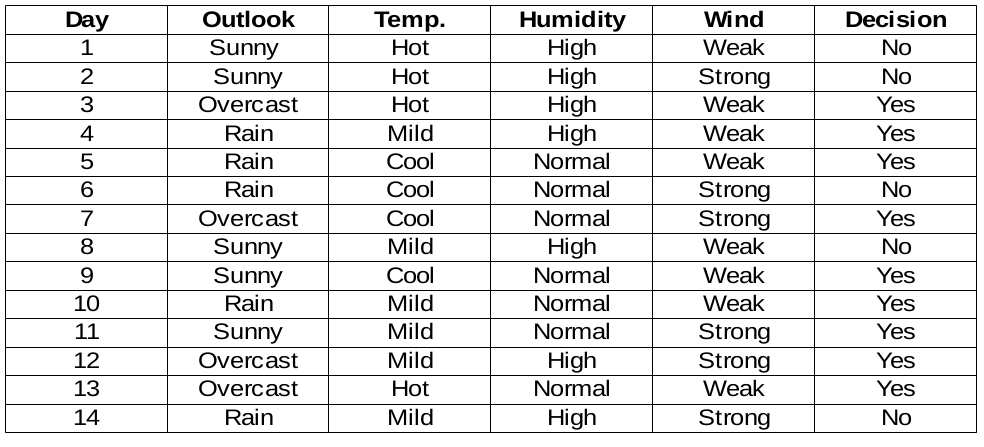
Nous allons construire des règles de décision pour l'ensemble de données suivant. La colonne de décision est la cible que nous aimerions trouver en fonction de certaines caractéristiques.
D'ailleurs, nous allons ignorer la colonne du jour car ce n'est que le numéro de ligne.
pour lire l'ensemble de données d'implémentation Python à partir du fichier CSV ci-dessous: –
importer des pandas au format pd
données = pd.read_csv("jeu de données.csv")
data.head()
Nous devons trouver la caractéristique la plus importante dans les colonnes cibles pour choisir le nœud pour diviser les données dans cet ensemble de données.
Caractéristique d'humidité
Il existe deux types de la classe présente dans les colonnes d'humidité: grand et normal. Nous allons maintenant calculer les valeurs du chi_carré pour eux.
| Oui | Non | Total | Attendu | Chi carré Oui | Khi deux Non | |
| Haute | 3 | 4 | 7 | 3,5 | 0,267 | 0,267 |
| bas | 6 | 1 | 7 | 3,5 | 1.336 | 1.336 |
pour chaque ligne, la colonne total est la somme des décisions oui et non. La moitié de la colonne totale est appelée valeurs attendues parce qu'il y a 2 classes en décision. Il est facile de calculer les valeurs du Khi deux sur la base de ce tableau..
Par exemple,
chi carré oui pour une humidité élevée est √ ((3– 3,5)2 / 3,5) = 0,267
alors que le vrai est 3 et l'attendu est 3,5.
Ensuite, la valeur du khi carré de la caractéristique d'humidité est
= 0,267 + 0,267 + 1,336 + 1,336
= 3.207
À présent, on trouvera aussi des valeurs du chi carré pour d'autres caractéristiques. La caractéristique avec la valeur maximale du chi carré sera le point de décision. Qu'en est-il de la fonction vent?
Caractéristique du vent
Il existe deux types de classe présents dans les colonnes de vent: faible et fort. Le tableau suivant est le tableau suivant.
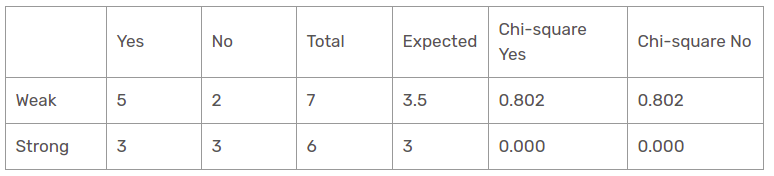
Ici, la valeur d'essai du khi carré de la caractéristique du vent est
= 0,802 + 0,802 + 0 + 0
= 1,604
Il s'agit également d'une valeur inférieure à la valeur du chi carré de l'humidité. Qu'en est-il de la fonction température?
caractéristique de température
Il existe trois types de classe présents dans les colonnes de température: chaud, froid et lisse. Le tableau suivant est le tableau suivant.
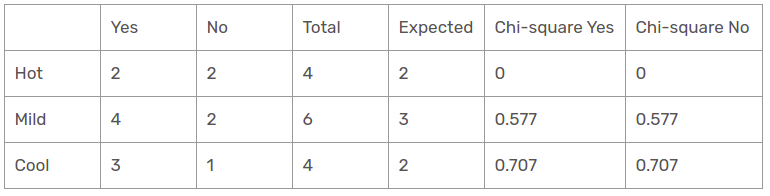
Ici, la valeur d'essai du khi carré de la caractéristique de température est
= 0 + 0 + 0,577 + 0,577 + 0,707 + 0,707
= 2.569
Il s'agit d'une valeur inférieure à la valeur du chi carré de l'humidité et également supérieure à la valeur du chi_carré du vent. Qu'en est-il de la fonction Outlook?
Fonctionnalité Outlook
Il existe trois types de classes présentes dans les colonnes de température: ensoleillé, pluvieux et nuageux. Le tableau suivant est le tableau suivant.
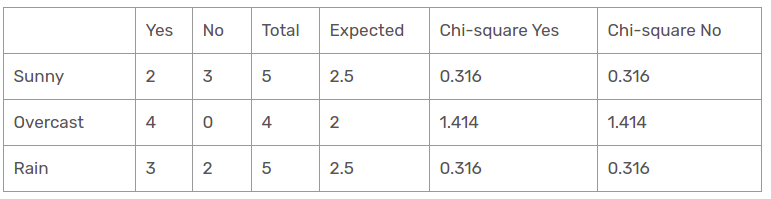
Ici, la valeur du test du chi carré de la fonction de perspective est
= 0,316 + 0,316 + 1,414 + 1,414 + 0,316 + 0,316
= 4.092
Nous avons calculé les valeurs du chi carré de toutes les caractéristiques. Voyons-les tous à une table.
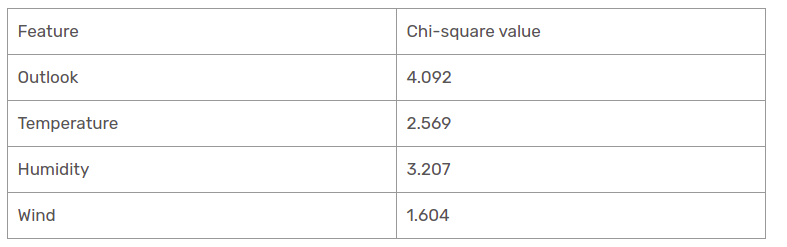
Comme on le voit, la colonne Outlook a la valeur chi-carré la plus élevée et la plus élevée. Cela implique que c'est la caractéristique principale du composant. Parallèlement à ces valeurs, nous allons placer cette fonctionnalité dans le nœud racine.
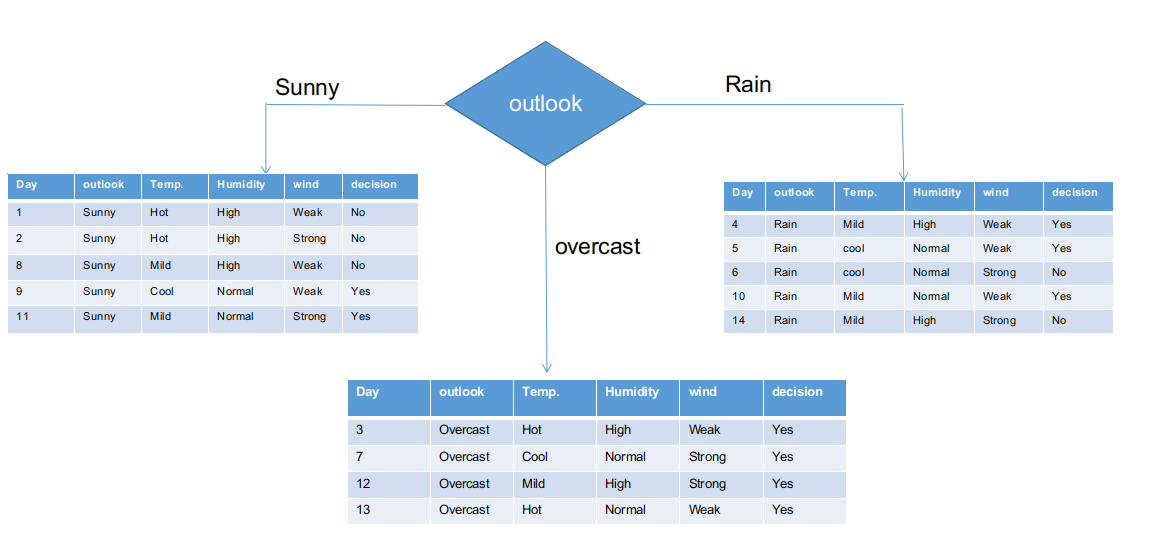
Nous avons séparé les informations brutes en fonction des classes Outlook dans l'illustration ci-dessus. Par exemple, la branche assombrie a simplement une décision affirmative sur l'ensemble de données de sous-information. Cela implique que l'arbre CHAID retourne OUI si le panorama est nuageux.
Les branches ensoleillées et pluvieuses ont des décisions oui et non. Nous appliquerons des tests du chi carré pour ces ensembles de données sous-informatives.
Outlook = branche ensoleillée
Cette branche a 5 exemples. Actuellement, nous recherchons la caractéristique la plus prédominante. D'ailleurs, nous allons ignorer la fonction Outlook maintenant, car ils sont tout à fait les mêmes. A la fin de la journee, nous trouverons les colonnes les plus prédominantes entre la température, humidité et vent.
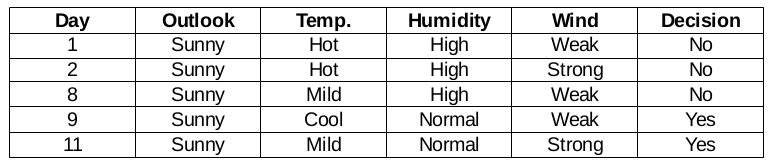
Fonction d'humidité pour quand le panorama est ensoleillé
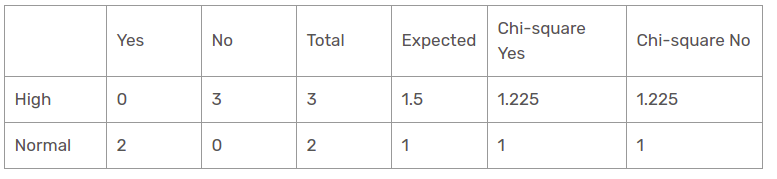
La valeur du khi carré de la caractéristique d'humidité pour une perspective ensoleillée est
= 1,225 + 1,225 + 1 + 1
= 4.449
Fonction vent lorsque le panorama est ensoleillé
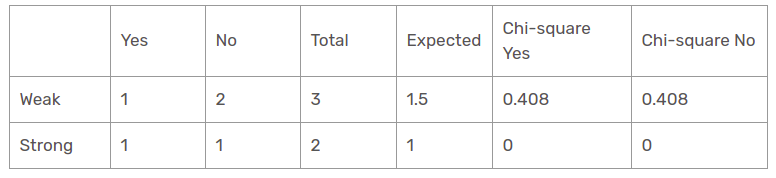
La valeur du khi carré de la caractéristique du vent pour une perspective ensoleillée est
= 0,408 + 0,408 + 0 + 0
= 0,816
Fonction température lorsque le panorama est ensoleillé
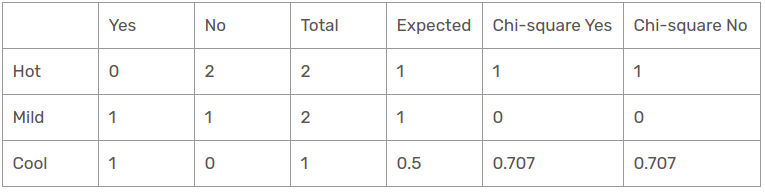
Ensuite, la valeur du khi carré de la caractéristique de température pour la perspective ensoleillée est
= 1 + 1 + 0 + 0 + 0,707 + 0,707
= 3.414
Nous avons trouvé des valeurs de chi carré pour la perspective ensoleillée. Voyons-les tous à une table.
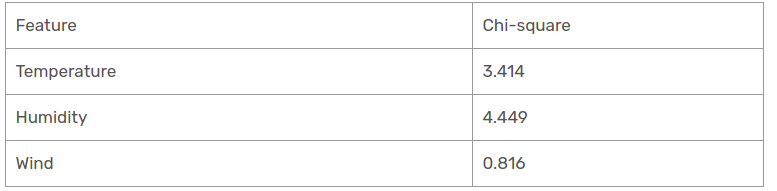
Actuellement, l'humidité est la caractéristique la plus prédominante de la branche ensoleillée du belvédère. Nous mettrons cette caractéristique en règle de décision.
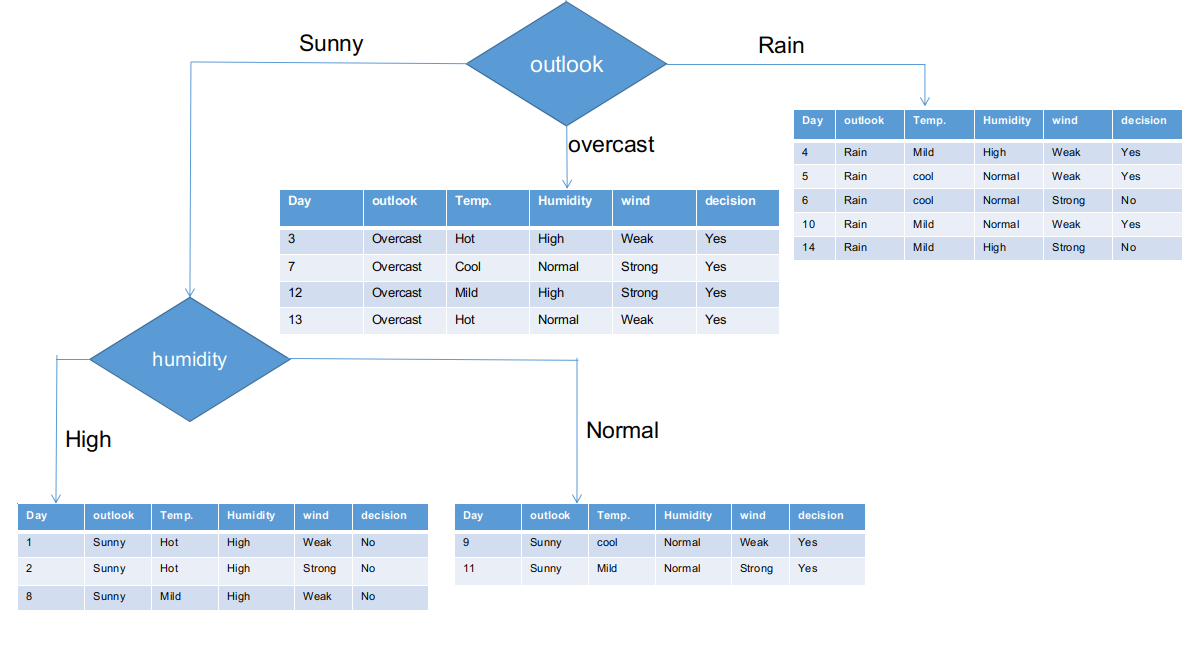
Actuellement, les deux branches d'humidité pour une perspective ensoleillée n'ont qu'une seule décision comme indiqué ci-dessus. L'arbre CHAID retournera NON pour une perspective ensoleillée et une humidité élevée et retournera OUI pour une perspective ensoleillée et une humidité normale.
Branche perspective pluie
En réalité, cette branche a à la fois des décisions positives et négatives. Nous devons appliquer le test du chi carré pour cette branche pour trouver une décision précise. Cette branche a 5 différentes instances, comme démontré dans l'ensemble de données de collecte de sous-informations ci-joint. Que diriez-vous de découvrir la caractéristique la plus prédominante entre la température, humidité et vent?
Fonction vent pour les prévisions de pluie
Il existe deux types d'une classe présente dans la caractéristique du vent pour la perspective de la pluie: faible et fort.
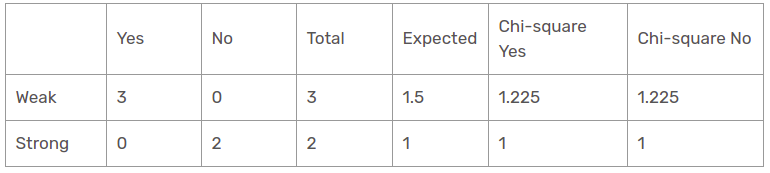
Ensuite, la valeur du khi carré de la caractéristique du vent pour la perspective de la pluie est
= 1,225 + 1,225 + 1 + 1
= 4.449
Fonction d'humidité pour les prévisions de pluie
Il existe deux types de classes présentes dans la caractéristique d'humidité pour la perspective de la pluie: grand et normal.
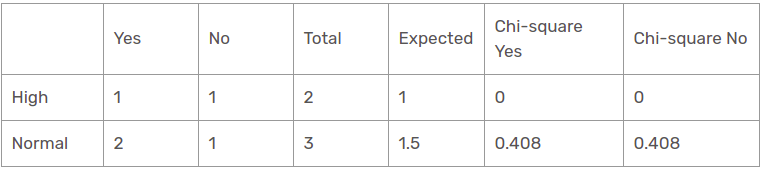
La valeur du chi carré de la caractéristique d'humidité pour la perspective de la pluie est
= 0 + 0 + 0.408 + 0.408
= 0,816
Caractéristique de température pour les prévisions de pluie
Il existe deux types de classes présentes dans les caractéristiques de température pour la perspective de pluie, comme chaud et frais.
La valeur du khi carré de la caractéristique de température pour la perspective de la pluie est
= 0 + 0 + 0.408 + 0.408
= 0,816
Nous avons constaté que toutes les valeurs du chi carré pour la pluie sont la branche perspective. Voyons-les tous à une table.
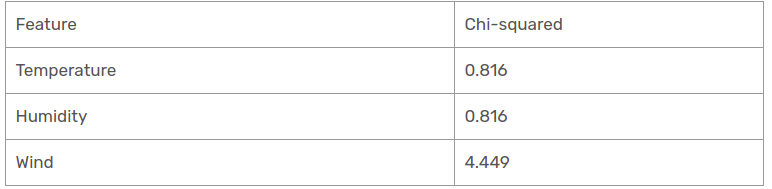
Donc, la fonction vent est la gagnante de la pluie est la branche de la perspective. Placez cette colonne dans la branche connectée et affichez le jeu de données sous-informatif correspondant.
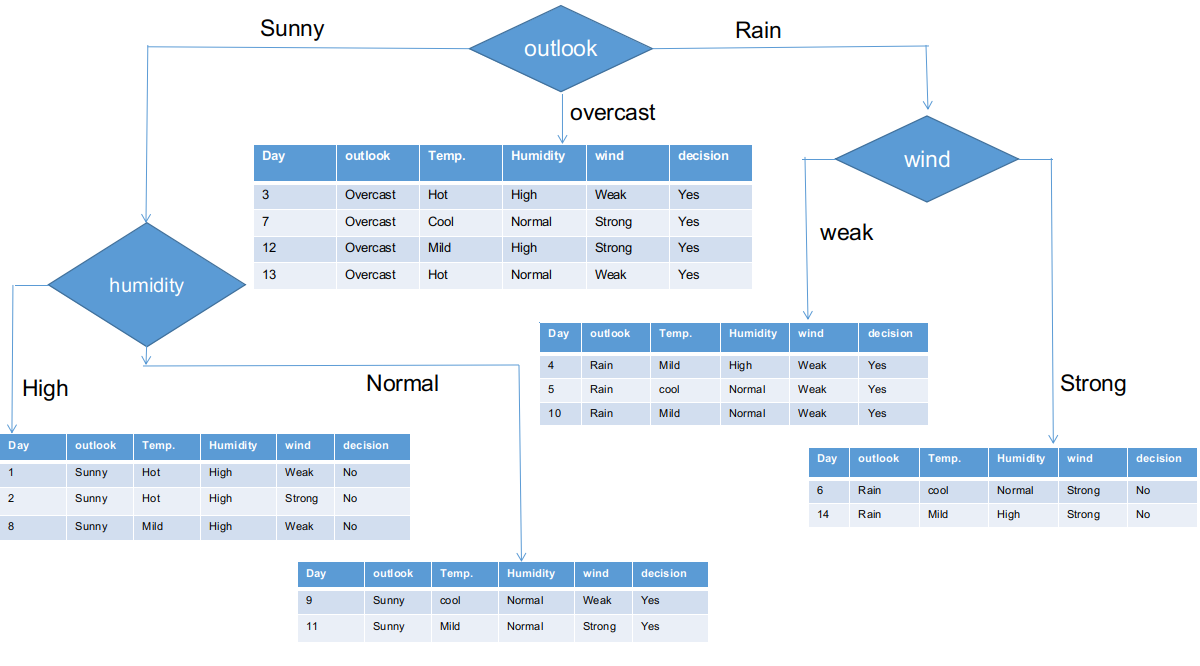
Comme on le voit, toutes les branches ont des ensembles de données sous-informatives avec une seule décision, comme oui ou non. De cette manière, nous pouvons générer l'arbre CHAID comme illustré ci-dessous.
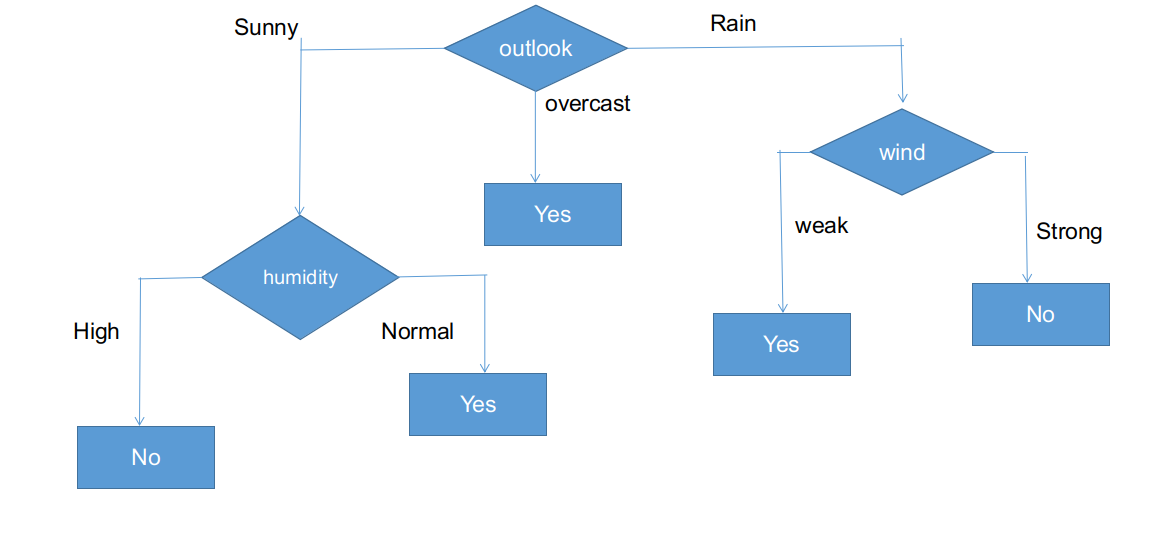
La forme finale de l'arbre CHAID.
Implémentation Python d'un arbre de décision à l'aide de CHAID
de chefboost importer Chefboost en tant que cb
importer des pandas au format pd
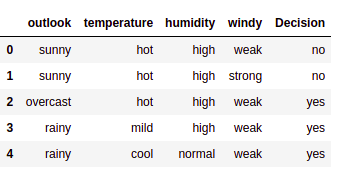
données = pd.read_csv("/accueil/kajal/Téléchargements/météo.csv")
data.head()
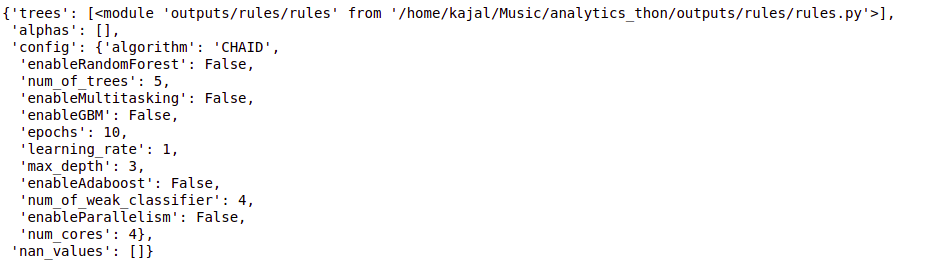
configuration = {"algorithme": "CHAID"}
arbre = cb.fit(Les données, configuration)
arbre
# instance_test = ['ensoleillé','chaud','haute','faible','non'] instance_test = data.iloc[2] instance_test
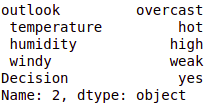
cb.predict(arbre,instance_test)
sortir:- 'Oui'
#obj[0]: perspectives, obj[1]: Température, obj[2]: humidité, obj[3]: venteux
# {"caractéristique": "perspectives", "instances": 14, "valeur_métrique": 4.0933, "profondeur": 1}
def findDécision(obj):
si obj[0] == 'pluie':
# {"caractéristique": " venteux", "instances": 5, "valeur_métrique": 4.4495, "profondeur": 2}
si obj[3] == 'faible':
return 'yes'
elif obj[3] == 'fort':
return 'no'
else:
return 'no'
elif obj[0] == 'ensoleillé':
# {"caractéristique": " humidité", "instances": 5, "valeur_métrique": 4.4495, "profondeur": 2}
si obj[2] == 'haut':
return 'no'
elif obj[2] == 'normal':
return 'yes'
else:
return 'yes'
elif obj[0] == 'couvert':
return 'yes'
else:
retourner 'oui'
conclusion
Donc, nous avons créé un arbre de décision CHAID de A à Z sur ce post. CHAID utilise une métrique de mesure du chi carré pour découvrir la caractéristique la plus importante et l'appliquer de manière récursive jusqu'à ce que les ensembles de données sous-informatifs aient une seule décision. Bien qu'il s'agisse d'un algorithme d'arbre de décision hérité, c'est toujours le même procédé pour trier les problèmes.
Les médias présentés dans cet article ne sont pas la propriété de DataPeaker et sont utilisés à la discrétion de l'auteur.
