Cet article a été publié dans le cadre du Blogathon sur la science des données.
introduction
Une méthode statistique populaire et largement utilisée pour la prévision des séries chronologiques est le modèle ARIMA.. Le lissage exponentiel et les modèles ARIMA sont les deux approches les plus largement utilisées pour la prédiction de séries chronologiques et fournissent des approches complémentaires au problème.. Alors que les modèles de lissage exponentiel sont basés sur une description de la tendance et de la saisonnalité des données, Les modèles ARIMA visent à décrire les autocorrélations dans les données.
Pour connaître la saisonnalité, regarde ce blog.
Avant de parler du modèle ARIMA, Parlons du concept de stationnarité et de la technique de différenciation des séries temporelles.
Stationnarité
Une donnée de série temporelle stationnaire est une donnée dont les propriétés ne dépendent pas du temps, d'où la série chronologique avec les tendances, ou avec saisonnalité, ils ne sont pas immobiles. la tendance et la saisonnalité affecteront la valeur de la série chronologique à différents moments. D'un autre côté, pour la stationnarité, peu importe quand vous le regardez, devrait être très similaire à tout moment. En général, une série chronologique stationnaire n'aura pas de modèles prévisibles à long terme.
ARIMA est un acronyme pour Auto-Regressive Integrated Moving Average. Il s'agit d'une classe de modèle qui capture un ensemble de différentes structures temporelles standard dans des données de séries chronologiques.
Dans ce tutoriel, nous parlerons de la façon de développer un modèle ARIMA pour la prévision de séries temporelles en Python.
Un modèle ARIMA est une classe de modèles statistiques pour l'analyse et la prévision de données de séries chronologiques. Il est vraiment simplifié au niveau de son utilisation. Cependant, ce modèle est vraiment puissant.
ARIMA signifie Auto-Regressive Integrated Moving Average.
Les paramètres du modèle ARIMA sont définis comme suit:
p: Le nombre d'observations de décalage incluses dans le modèle, aussi appelé ordre de décalage.
ré: Le nombre de fois où les observations brutes diffèrent, aussi appelé degré de différence.
q: La taille de la fenêtre de moyenne mobile, aussi appelé ordre de moyenne mobile.
Un modèle de régression linéaire est construit qui inclut le nombre et le type de termes spécifiés, et les données sont préparées par un degré de différenciation pour les rendre stationnaires, c'est-à-dire, éliminer les structures tendancielles et saisonnières qui nuisent au modèle de régression.
ESCALIER
1. Afficher les données des séries chronologiques
2. Identifiez si la date est stationnaire
3. Tracer les graphiques de corrélation et de corrélation automatique
4. Construire le modèle ARIMA ou ARIMA saisonnier basé sur les données
Commençons
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
Dans ce tutoriel, J’utilise le jeu de données suivant.
df=pd.read_csv(« time_series_data.csv »)
df.head()
# Updating the header
df.columns=["Mois","Ventes"]
df.head()
df.décrire()
df.set_index('Mois',inplace=Vrai)
à partir de pylab importer rcParams
rcParams['figure.figsize'] = 15, 7
df.plot()
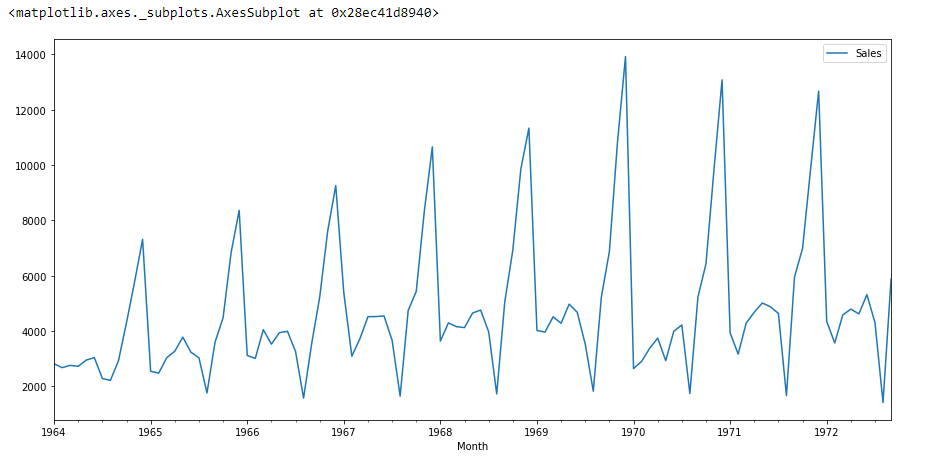
si nous regardons le graphique ci-dessus, nous pouvons trouver une tendance selon laquelle il y a un moment où les ventes sont élevées et vice versa. Cela signifie que nous pouvons voir que les données suivent la saisonnalité.. Pour ARIMA, la première chose que nous faisons est d'identifier si les données sont stationnaires ou non stationnaires. si les données ne sont pas stationnaires, nous allons essayer de les rendre stationnaires et ensuite traiter plus.
Vérifions que si l'ensemble de données donné est stationnaire ou non, pour cela on utilise adfuller.
de statsmodels.tsa.stattools import adfuller
J'ai importé l'adfuller en exécutant le code ci-dessus.
test_result=adfuller(df['Ventes'])
Pour identifier la nature des données, on utilisera l'hypothèse nulle.
H0: L'hypothèse nulle: Il s'agit d'une déclaration sur la population qui est considérée comme vraie ou utilisée pour argumenter, à moins qu'il ne puisse être démontré qu'elle est incorrecte au-delà de tout doute raisonnable..
H1: L'hypothèse alternative: C'est une déclaration sur la population qui contredit H0 et ce que nous concluons lorsque nous rejetons H0.
#Ho: il n'est pas immobile
# H1: est arrêté
Nous considérerons l'hypothèse nulle que les données ne sont pas stationnaires et l'hypothèse alternative que les données sont stationnaires.
def adfuller_test(Ventes):
result=adfuller(Ventes)
étiquettes = ['Statistique de test ADF','valeur p','#Lags Utilisé',« Nombre d'observations »]
pour la valeur,étiquette en zip(résultat,Étiquettes):
imprimer(label+' : '+str(valeur) )
si résultat[1] <= 0.05:
imprimer("des preuves solides contre l’hypothèse nulle(Ho), rejeter l’hypothèse nulle. Les données sont stationnaires")
autre:
imprimer("faibles preuves contre l’hypothèse nulle,indiquant qu’il n’est pas stationnaire ")
adfuller_test(df['Ventes'])
Après avoir exécuté le code ci-dessus, nous obtiendrons la valeur P,
Statistiques de test ADF : -1.8335930563276237 valeur p : 0.3639157716602447 #Décalages utilisés : 11 Nombre d’observations : 93
Ici, la valeur P est 0.36, qui est supérieur à 0.05, ce qui signifie que les données acceptent l’hypothèse nulle, ce qui signifie que les données ne sont pas stationnaires.
Essayons de voir la première différence et la différence saisonnière:
df[« Les ventes d’abord la différence »] = df['Ventes'] - df['Ventes'].décalage(1) df[« Première différence saisonnière »]=df['Ventes']-df['Ventes'].décalage(12) df.head()
# Again testing if data is stationary
adfuller_test(df[« Première différence saisonnière »].tomber())
Statistiques de test ADF : -7.626619157213163
valeur p : 2.060579696813685e-11
#Lags Used : 0
Nombre d’observations : 92
Ici, la valeur P est 2.06, ce qui signifie que nous rejetterons l’hypothèse nulle. Ensuite, les données sont stationnaires.
df[« Première différence saisonnière »].terrain()
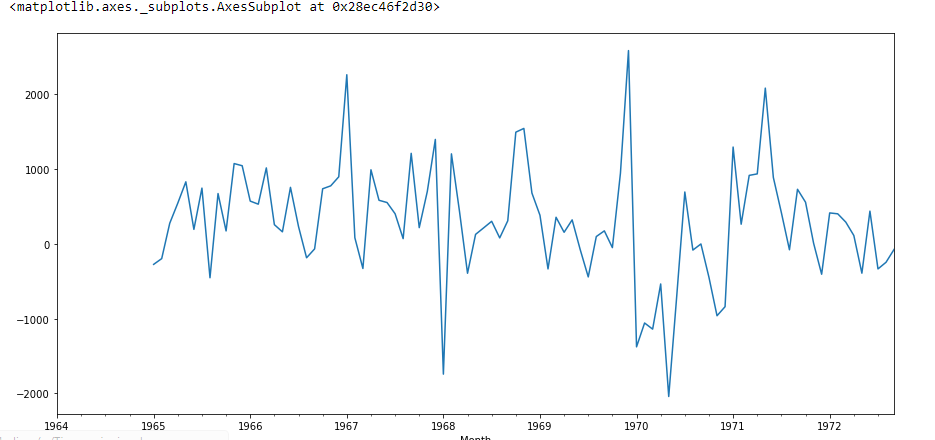
Je vais créer une autocorrélation:
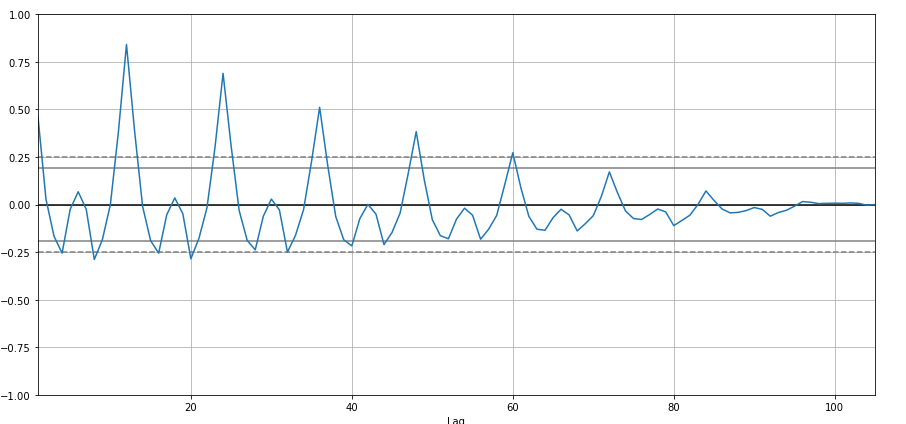
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(df['Ventes'])
plt.show()
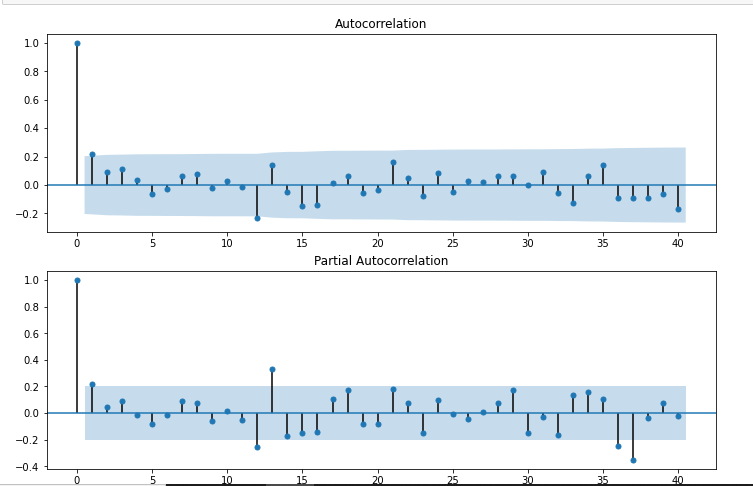
à partir de statsmodels.graphics.tsaplots importer plot_acf,plot_pacf
import statsmodels.api as sm
fig = plt.figure(taille de la figue=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df[« Première différence saisonnière »].tomber(),décalages=40,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df[« Première différence saisonnière »].tomber(),lags=40,ax=ax2)
# For non-seasonal data #p=1, d=1, q=0 ou 1 from statsmodels.tsa.arima_model import ARIMA model=ARIMA(df['Ventes'],commande=(1,1,1)) model_fit=model.fit() model_fit.résumé()
| Dep. Variable: | ré. Ventes | Non. Observations: | 104 |
|---|---|---|---|
| Modèle: | ARIMA (1, 1, 1) | Probabilité logarithmique | -951.126 |
| Méthode: | css-mle | SD de innovaciones | 2227.262 |
| Date: | Mié, 28 oct 2020 | AIC | 1910.251 |
| Conditions météorologiques: | 11:49:08 | BIC | 1920.829 |
| Spectacles: | 02-01-1964 | HQIC | 1914.536 |
| – 09-01-1972 |
| coef | std err | Avec | P> | Avec | | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| constant | 22.7845 | 12.405 | 1.837 | 0.066 | -1.529 | 47.098 |
| Ar. L1. D.Ventes | 0.4343 | 0,089 | 4.866 | 0.000 | 0,259 | 0,609 |
| maman. L1. D.Ventes | -1,0000 | 0,026 | -38.503 | 0.000 | -1.051 | -0,949 |
| Vrai | Imaginario | Module | La fréquence | |
|---|---|---|---|---|
| AR.1 | 2.3023 | + 0,0000j | 2.3023 | 0,0000 |
| MA.1 | 1,0000 | + 0,0000j | 1,0000 | 0,0000 |
df[« prévision »]=model_fit.prédire(début=90,fin=103,dynamique=Vrai) df[['Ventes',« prévision »]].terrain(taille de la figue=(12,8))
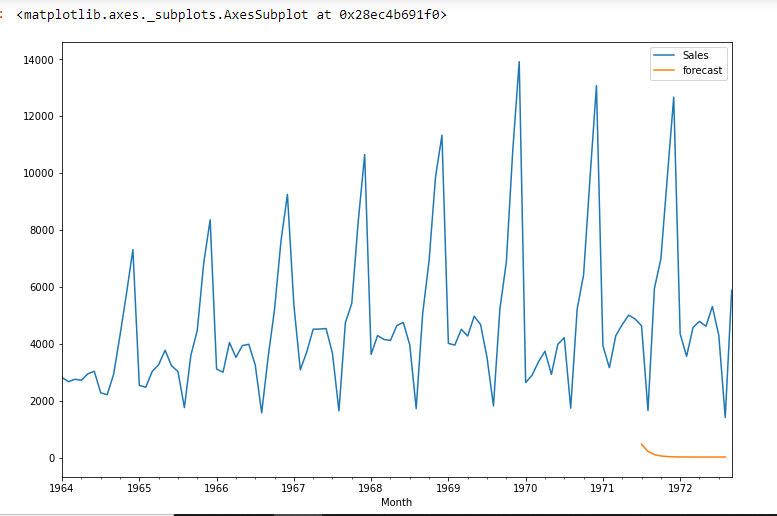
import statsmodels.api as sm
model=sm.tsa.statespace.SARIMAX(df['Ventes'],commande=(1, 1, 1),seasonal_order=(1,1,1,12))
résultats=model.fit()
df[« prévision »]=résultats.prédire(début=90,fin=103,dynamique=Vrai)
df[['Ventes',« prévision »]].terrain(taille de la figue=(12,8))
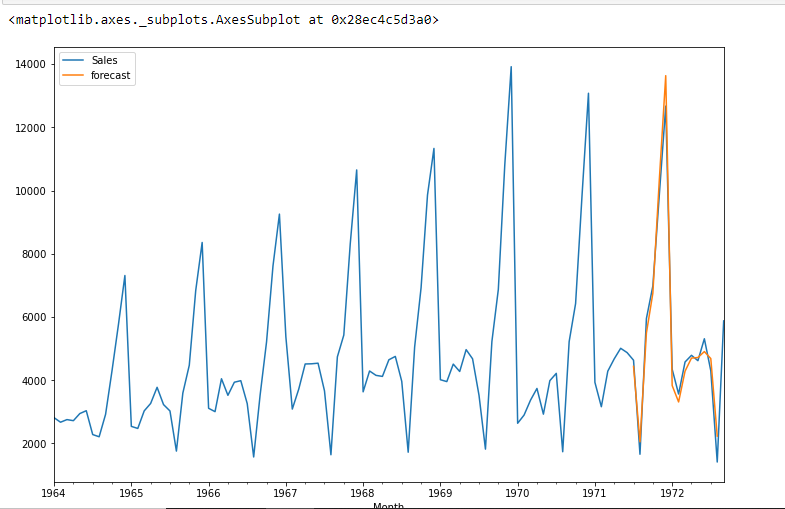
from pandas.tseries.offsets import DateOffset
future_dates=[df.index[-1]+ DateOffset(mois=x)pour x dans la plage(0,24)]
future_datest_df=pd. DataFrame(index=future_dates[1:],colonnes=df.colonnes)
future_datest_df.tail()
future_df=pd.concat([df,future_datest_df])
future_df[« prévision »] = résultats.prédire(commencer = 104, fin = 120, dynamique = vrai)
future_df[['Ventes', « prévision »]].terrain(taille de la figue=(12, 8))
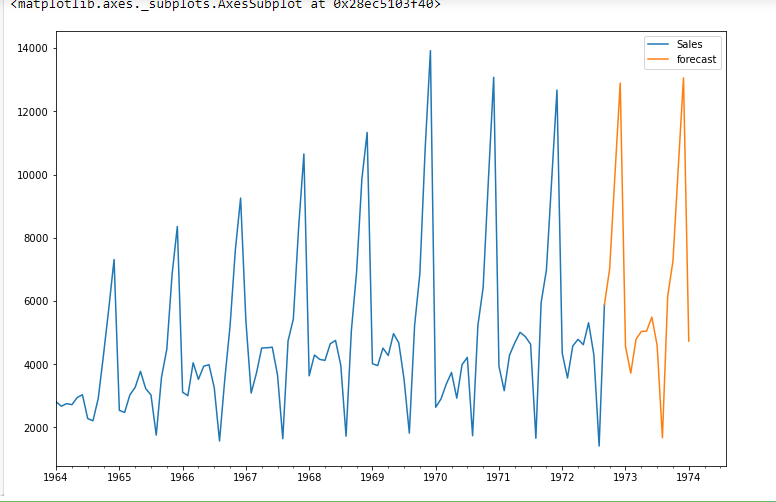
conclusion
La prévision des séries chronologiques est vraiment utile lorsque nous devons prendre des décisions futures ou que nous devons faire des analyses, nous pouvons le faire rapidement en utilisant ARIMA, il existe de nombreux autres modèles à partir desquels nous pouvons faire des prévisions de séries chronologiques, mais ARIMA est vraiment facile à comprendre.
J'espère que cet article vous aidera et vous fera gagner du temps. Laissez-moi savoir si vous avez des suggestions..
CODAGE HEUREUX.
Prabhat Pathak (Profil LinkedIn) est un analyste principal.
