fonction de coût | Types d'apprentissage automatique de la fonction de coût

Cet article a été publié dans le cadre du Blogathon sur la science des données.

Crédit: https://GIFER.com/fr/GxlE

Le 2 les principales questions qui me sont venues à l'esprit en travaillant sur cet article étaient “Pourquoi j'écris cet article?” & “En quoi mon article est-il différent des autres articles?” Bon, la fonction de coût est un concept important à comprendre dans les domaines de la science des données, mais pendant que je poursuivais mes études supérieures, Je me suis rendu compte que les ressources disponibles en ligne sont trop générales et ne couvrent pas entièrement mes besoins.

J'ai dû parcourir de nombreux articles et regarder quelques vidéos sur YouTube pour avoir une idée des fonctions de coût. Par conséquent, Je voulais combiner les fonctions “Quoi”, “Lorsque”, “Comment” Oui “Parce que” du coût qui peut aider à expliquer ce sujet plus clairement. J'espère que mon article agira comme un guichet unique pour les fonctions de coût !!

Guide factice de la fonction de coût 🤷‍♀️

Fonction de perteLa fonction de perte est un outil fondamental de l’apprentissage automatique qui quantifie l’écart entre les prédictions du modèle et les valeurs réelles. Son but est de guider le processus de formation en minimisant cette différence, permettant ainsi au modèle d’apprendre plus efficacement. Il existe différents types de fonctions de perte, tels que l’erreur quadratique moyenne et l’entropie croisée, chacun adapté à différentes tâches et...: se utiliza cuando nos referimos al error de un solo ejemplo de entraînementLa formation est un processus systématique conçu pour améliorer les compétences, connaissances ou aptitudes physiques. Il est appliqué dans divers domaines, Comme le sport, Éducation et développement professionnel. Un programme d’entraînement efficace comprend la planification des objectifs, Pratique régulière et évaluation des progrès. L’adaptation aux besoins individuels et la motivation sont des facteurs clés pour obtenir des résultats réussis et durables dans toutes les disciplines.....
fonction de coût: est utilisé pour référencer une moyenne des fonctions de perte sur l'ensemble d'un ensemble de données d'apprentissage.

Mais, * parce que * utiliser une fonction de coût?

Pourquoi diable avons-nous besoin d'une fonction de coût? Considérons un scénario où nous voulons classer les données. Supposons que nous ayons les détails de taille et de poids de certains chiens et chats. utilisons-les 2 caractéristiques pour les classer correctement. Si nous traçons ces enregistrements, obtenemos el siguiente Diagramme de dispersionLe nuage de points est un outil graphique utilisé en statistiques pour visualiser la relation entre deux variables. Il se compose d’un ensemble de points dans un plan cartésien, où chaque point représente une paire de valeurs correspondant aux variables analysées. Ce type de graphique vous permet d’identifier des modèles, Tendances et corrélations possibles, faciliter l’interprétation des données et la prise de décision sur la base des informations visuelles présentées....:

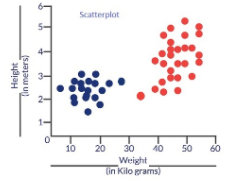
Figure 1: Nuage de points pour la taille et le poids de divers chiens et chats

Les points bleus sont des chats et les points rouges sont des chiens.. Voici quelques solutions au problème de classification ci-dessus.

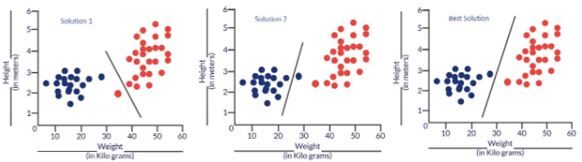
Figure: Solutions probables à notre problème de classification

Essentiellement, les trois classificateurs ont une très grande précision, mais la troisième solution est la meilleure car elle ne méconnaît aucun point. La raison pour laquelle il classe parfaitement tous les points est que la ligne est presque exactement entre les deux groupes et n'est pas plus proche de l'un ou l'autre groupe. C'est là qu'intervient le concept de fonction de coût.. La fonction de coût nous aide à atteindre la solution optimale. La fonction de coût est la technique d'évaluation “les performances de notre algorithme / maquette”.

Il prend à la fois les résultats prédits par le modèle et les résultats réels, et calculer à quel point le modèle s'est trompé dans sa prédiction. Produit un nombre plus élevé si nos prévisions diffèrent considérablement des valeurs réelles. UNE mesureLa "mesure" C’est un concept fondamental dans diverses disciplines, qui fait référence au processus de quantification des caractéristiques ou des grandeurs d’objets, phénomènes ou situations. En mathématiques, Utilisé pour déterminer les longueurs, Surfaces et volumes, tandis qu’en sciences sociales, il peut faire référence à l’évaluation de variables qualitatives et quantitatives. La précision des mesures est cruciale pour obtenir des résultats fiables et valides dans toute recherche ou application pratique.... que ajustamos nuestro modelo para mejorar las predicciones, la fonction de coût agit comme un indicateur de l'amélioration du modèle. Il s'agit essentiellement d'un problème d'optimisation. Les stratégies d'optimisation visent toujours à "minimiser la fonction de coût".

Types de fonction de coût

Il existe de nombreuses fonctions de coût dans l'apprentissage automatique et chacune a ses cas d'utilisation selon qu'il s'agit d'un problème de régression ou d'un problème de classification..

1. Fonction de coût de régression
2. Fonctions de coût de classification binaire
3. Fonctions de coût de classification à plusieurs classes

1. Fonction de coût de régression:

Les modèles de régression tentent de prédire une valeur continue, par exemple, le salaire d'un employé, le prix d'une voiture, prévoir un prêt, etc. Une fonction de coût utilisée dans le problème de régression est appelée “Fonction de coût de régression”. Ils sont calculés sur l'erreur basée sur la distance comme suit:

Erreur = y-y ‘

Où,

Oui – entrée réelle

Y'- Départ prévu

Les fonctions de coût de régression les plus utilisées sont ci-dessous,

1.1 erreur moyenne (MOI)

• Dans cette fonction de coût, l'erreur est calculée pour chaque donnée d'apprentissage, puis la valeur moyenne de toutes ces erreurs est dérivée.
• Le calcul de la moyenne des erreurs est le moyen le plus simple et le plus intuitif possible.
• Les erreurs peuvent être à la fois négatives et positives. Donc, peuvent s'annuler pendant l'addition, ce qui donne une erreur moyenne nulle pour le modèle.
• Donc, ce n'est pas une fonction de coût recommandée, mais cela jette les bases d'autres fonctions de coût des modèles de régression.

1.2 Erreur quadratique moyenne (MSE)

• Cela améliore l'inconvénient que nous avons trouvé dans l'erreur intermédiaire ci-dessus. Ici, un carré de la différence entre la valeur réelle et la valeur prédite est calculé pour éviter toute possibilité d'erreur négative.
• Il est mesuré comme la moyenne de la somme des écarts au carré entre les prédictions et les observations réelles..

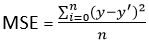
MSE = (somme des carrés des erreurs) / m

• Aussi connu sous le nom de perte L2.
• En MSE, puisque chaque erreur est au carré, aide à pénaliser même les petits écarts de prédiction par rapport à MAE. Mais si notre ensemble de données contient des valeurs aberrantes qui contribuent à des erreurs de prédiction plus importantes, donc la mise au carré de cette erreur amplifie encore l'erreur plusieurs fois et conduit également à une erreur MSE plus élevée.
• Donc, on peut dire qu'il est moins robuste aux valeurs aberrantes.

1.3 Erreur absolue moyenne (BEAUCOUP)

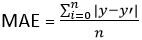
MAE = (somme des erreurs absolues) / m

2. Fonctions de coût pour les problèmes de classification

Les fonctions de coût utilisées dans les problèmes de classification sont différentes de celles utilisées dans le problème de régression.. Une fonction de perte couramment utilisée pour la classification est la perte d'entropie croisée. Comprenons l'entropie croisée avec un petit exemple. Considérons que nous avons un problème de classification de 3 classes comme suit.

Classe (Orange, Pomme, tomate)

Le modèle d'apprentissage automatique donnera une distribution de probabilité de ces 3 classes comme sortie pour une donnée d'entrée donnée. La classe avec la probabilité la plus élevée est considérée comme une classe gagnante pour la prédiction.

Salide = [P(Orange),P(Pomme),P(Tomate)]

La distribution de probabilité réelle pour chaque classe est indiquée ci-dessous.

Orange = [1,0,0]

pomme = [0,1,0]

tomate = [0,0,1]

Oui pendant la phase de formation, la classe d'entrée est Tomate, la distribution de probabilité prédite devrait tendre vers la distribution de probabilité réelle de Tomate. Si la distribution de probabilité prédite n'est pas plus proche de la distribution réelle, le modèle doit ajuster son poids. C'est là que l'entropie croisée devient un outil pour calculer la distance entre la distribution de probabilité prédite et la distribution réelle.. En d'autres termes, l'entropie croisée peut être considérée comme un moyen de mesurer la distance entre deux distributions de probabilité. L'image ci-dessous illustre l'intuition derrière l'entropie croisée:

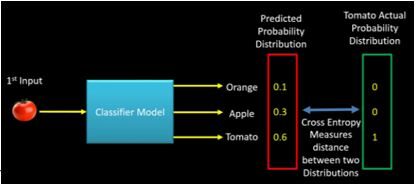
CHIFFRE"Chiffre" est un terme utilisé dans divers contextes, De l’art à l’anatomie. Dans le domaine artistique, fait référence à la représentation de formes humaines ou animales dans des sculptures et des peintures. En anatomie, désigne la forme et la structure du corps. En outre, en mathématiques, "chiffre" Il est lié aux formes géométriques. Sa polyvalence en fait un concept fondamental dans de multiples disciplines.... 3: L'intuition derrière l'entropie croisée (crédit – machinelearningknowledge.ai)

Ce n'était qu'une intuition derrière l'entropie croisée. Il est issu de la théorie de l'information.. À présent, avec cette compréhension de l'entropie croisée, regardons maintenant les fonctions de coût de classification.

2.1 Fonctions de coût de classification à plusieurs classes

Cette fonction de coût est utilisée dans les problèmes de classification où il existe plusieurs classes et les données d'entrée appartiennent à une seule classe.. Comprenons maintenant comment l'entropie croisée est calculée. Supposons que le modèle donne la distribution de probabilité comme indiqué ci-dessous pour 'n’ classes et pour une entrée particulière D.

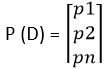
Et la distribution de probabilité réelle ou cible des données D est

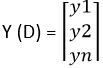
Alors, l'entropie croisée pour cette donnée particulière D est calculée comme

Perte d'entropie croisée (Oui, p) = – Oui^T Inscription (p)

= – (Oui₁ Journal (p₁) + Oui₂ Journal (p₂) + …… y_Nord Journal (p_Nord))

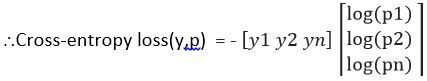
Définissons maintenant la fonction de coût en utilisant l'exemple précédent (Veuillez vous référer à l'image d'entropie croisée -Fig3),

p (tomate) = [0.1, 0.3, 0.6]

Oui (tomate) = [0, 0, 1]

Entropie croisée (ré) = – Oui * Journal (p) quand y = 1

Entropie croisée (ré) = – (1-Oui) * Journal (1-p) quand y = 0

Entropie croisée binaire = (Somme d'entropie croisée pour les données N) / N

conclusion

En rapport