Simulation de Monte-Carlo | Effectuer une simulation de Monte Carlo dans R

Cet article a été publié dans le cadre du Blogathon sur la science des données.

introduction

Cet article a pour objectif de présenter la simulation Monte Carlo pour l'analyse des incertitudes variables. Monte Carlo peut remplacer la propagation d'erreurs car il surmonte les inconvénients de la propagation d'erreurs. nous discuterons:

• Comment propager l'erreur;
• Pourquoi utiliser Monte Carlo au lieu de la propagation d'erreurs? Oui
• Les étapes pour réaliser l'incertitude de Monte Carlo.

Commençons cette discussion par des choses simples. Combien un employé de City A dépense-t-il en frais de subsistance en un mois? Il y a des milliers d'employés dans la ville A avec des frais de subsistance différents. Pour répondre à la question précédente, nous devons demander à plusieurs employés et enregistrer leurs réponses. Ces employés réagiront différemment. Vos frais de subsistance varieront selon une distribution de probabilité. Bien que nous n'ayons pas les ressources pour demander à tous les employés, nous pouvons échantillonner un groupe de, par exemple, 50 employés afin que l'enquête représente la population.

Cependant, nous avons encore besoin d'un nombre pour représenter le total des frais de subsistance. Disons que nous obtenons que les frais de subsistance mensuels moyens sont $ 2000. Ou bien, une autre façon est d'utiliser la médiane pour représenter les dépenses totales. Pour exprimer d'autres frais de subsistance possibles, on peut utiliser l'écart type. Par exemple, les dépenses de subsistance mensuelles dans la ville A sont $ 2000 ± 500 (moyenne ± écart type).

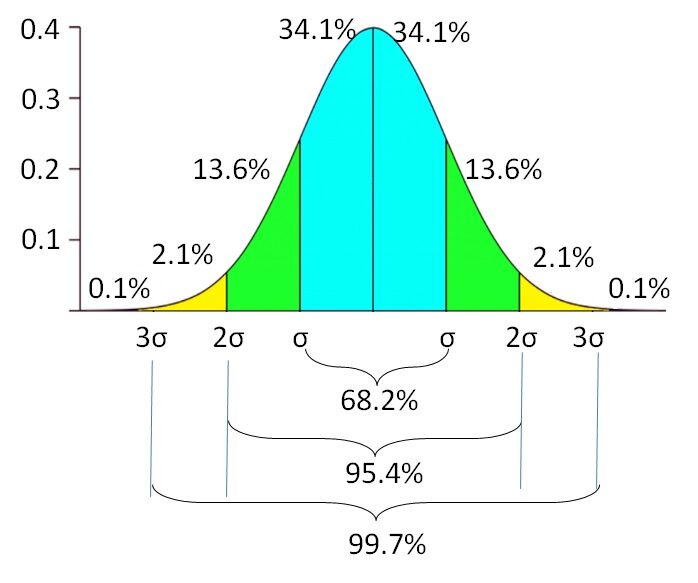
Cela signifie que si les données sont normalement distribuées, les 68,2% des employés dépensent entre $ 1500 Oui $ 2500. Il y a un autre 31,8% des employés qui dépensent moins de $ 1500 et plus de $ 2500 en frais de subsistance mensuels. La probabilité de dépenses de vie diminue à mesure qu'elle s'éloigne de la moyenne. Il y a une probabilité de 0,1% de trouver des employés dont les frais de subsistance sont inférieurs à $ 500 le supérieur à $ 3500. L'écart-type reflète l'incertitude variable de la charge de vie. Indique l'étendue inférieure et supérieure de la variable, au lieu de se fier à une seule valeur.

Propagation d'erreur

Puisque les employés de la ville A ont un revenu: $ 3200 ± 2000, frais de subsistance: $ 2000 ± 500, crédit: $ 180 ± 130, revenus ou dépenses imprévus: $ 20 ± 300 et taux d'intérêt bancaire: 0,85 ± 0,35% mensuel. Nous voulons calculer combien un employé peut économiser en un mois. L'équation est exprimée ci-dessous:

Économies = (Revenu – Frais de subsistance – Crédit + Revenu / dépenses imprévues) × (1 + Intérêts)

L'épargne mensuelle est calculée comme le revenu total déduit des frais de subsistance et du crédit et ajouté aux revenus ou dépenses imprévus.. Après un mois, augmentation de l'épargne nominale due aux intérêts bancaires. Nous calculerons les économies mensuelles moyennes et l'incertitude. Regardez l'équation suivante sur la façon de calculer l'incertitude.

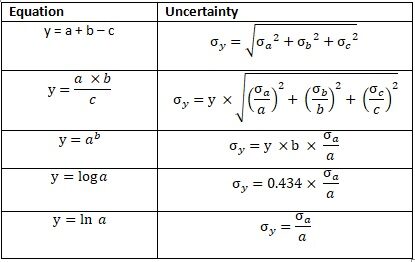
Fig. 2 Propagation d'erreur

Économie1 = ((3200 ± 2000) - (2000 ± 500) - (180 ± 130) + (20 ± 300)) × (1 + (0.0085 ± 0.0035))

Économie1 = 1040 ±Enregistrement_1

??Enregistrement_1 = ((20002 + 5002 + 1302 + 20002))0.5

??Enregistrement_1 = 2087

Économie1 ± σEnregistrement_1 = 1040 ± 2087

Celui-ci calcule les économies mensuelles après comptabilisation des intérêts bancaires.

Économie = Économie1 × (1 + (0.0085 ± 0.0035)) 

Sauvegarde = (1040 ± 2087) × (1.0085 ± 0.0035)

Sauvegarde = 1049 ±Sauvegarde_2

??Économie = 1049 × ((2087/1040)2 + (0.0035/1.0085)2)0.5

??Économie = 1049 × 2.01

??Économie = 2105

Économies ± σ_Économie = 1049 ± 2105

Du résultat, on peut voir ça, En moyenne, les gens peuvent économiser $ 1049 dans un mois avec l'incertitude de $ 2105. La limite inférieure de l'épargne mensuelle est – $ 1056 ($ 1049 – $ 2105), qu'est-ce qu'une valeur négative. L'incertitude elle-même est 2105, Qu'est que c'est 2 fois supérieure à la valeur moyenne. Si nous visualisons le graphique, on voit que l'épargne salariale va de – $ 6000 Oui $ 8000. Cela semble étrange car les limites inférieure et supérieure sont presque équilibrées. Je crois que, en réalité, le montant de l'épargne doit avoir une plus grande variabilité que le montant du déficit.

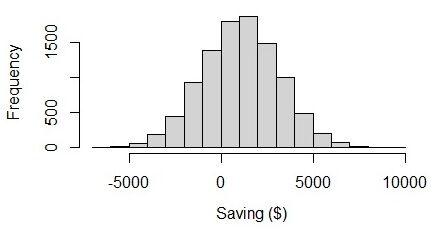
Fig. 3 Visualisation des économies dans une distribution normale

Comment cela se passe-t-il? Le problème réside dans les données sur les revenus. Le revenu de $ 3200 ± 2000 a une forte incertitude en raison de la variabilité des revenus. L'incertitude est supérieure à un tiers de la valeur moyenne. Si nous supposons qu'il s'agit d'une distribution normale, nous verrons que le 4.8% de la population a des revenus inférieurs 0, ce qui ne semble pas susceptible d'arriver. En réalité, le revenu doit toujours être supérieur à % 0. Ce problème se produit lorsque nous supposons que toutes les variables sont normalement distribuées, mais en réalité ils ne sont pas.

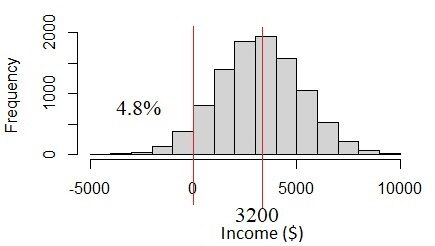
Fig. 4 Distribution normale si l'écart type du revenu est trop grand

Simulation de Monte-Carlo

Qui est la solution? Une autre façon d'évaluer l'incertitude est d'appliquer la simulation de Monte Carlo. Monte Carlo est à l'origine le nom d'une zone administrative à Monaco. Mais le Monte Carlo dans notre discussion d'aujourd'hui est un truc statistique.. Monte Carlo peut surmonter l'inconvénient de la propagation des erreurs. La simulation de Monte-Carlo, par opposition à la propagation d'erreur, peut travailler sur une distribution de données autre que la distribution normale et sur des données avec un grand écart type.

Fig. 5 Monte-Carlo à Monaco. La source: Google Map

La simulation Monte Carlo simule ou génère un ensemble de nombres aléatoires en fonction de la distribution des données et des paramètres de chaque variable. Une fois généré, toutes les valeurs des variables sont calculées à l'aide de l'équation. Cela semble un peu plus compliqué que d'utiliser la propagation d'erreur. Mais utilisez des outils de science des données, comme Python ou R, ce sera très simple. Dans cette discussion, nous allons démontrer l'utilisation du langage statistique R.

Étapes pour effectuer une simulation de Monte Carlo

1. Vérifier la fonction de densité de probabilité de la distribution des données.

Disons que nous examinons l'enregistrement de données fourni par l'enquête auprès des 50 interrogé. Il existe de nombreux types de fonctions de densité de probabilité et nous devons déterminer laquelle correspond à nos données. Les variables à distribution normale ne sont que les frais de subsistance et les revenus ou dépenses imprévus. La distribution des données sur le revenu est positive.

Dans ce cas, nous le traiterons comme une distribution gamma. C'est pourquoi la moyenne et l'étalement de l'erreur ne conviennent pas à ces données.. Les deux autres variables n'ont pas non plus de distribution normale.. Le taux d'intérêt bancaire est également réparti entre 0,3 Oui 1,5.

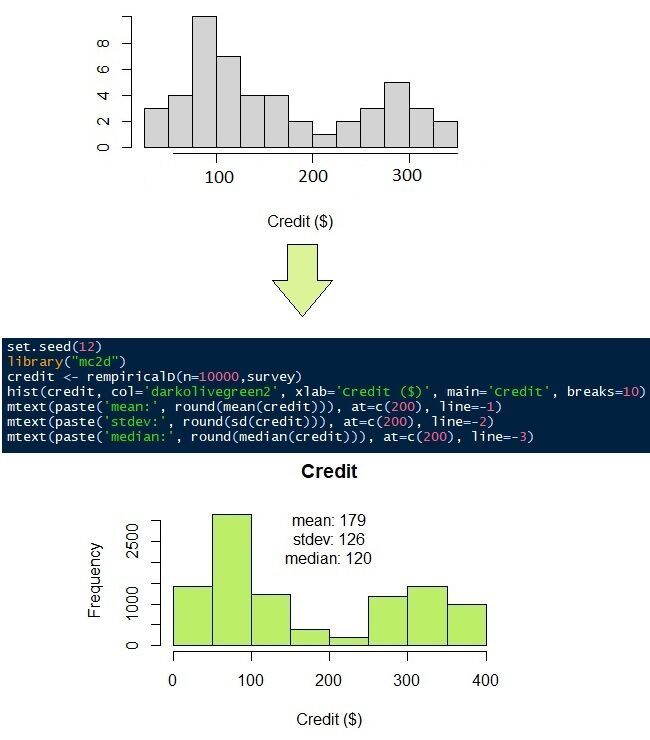
La distribution des données sur les prêts pour rembourser un crédit est assez unique. Les données sont principalement réparties en deux groupes de population. Le premier groupe a moins de crédit que le second. Disons que la distribution des données de crédit ne correspond à aucune fonction de densité de probabilité. Alors, nous utiliserons une distribution non paramétrique.

2. Générer une simulation Monte Carlo

Générer une simulation Monte Carlo signifie générer un ensemble de nombres aléatoires avec la même distribution de données que les données d'origine. Pour faire ceci, on fixe simplement le nombre de simulations et les paramètres de distribution selon le type de distribution. Nous fixons le nombre de simulations à 10,000. Cela signifie que nous allons simuler les données de 50 interrogé dans 10,000 Les données.

Les paramètres de la distribution normale sont la moyenne / moyenne et écart type. Nous savons que les moyennes ± écarts types des frais de subsistance et des revenus ou résultats inattendus sont 2000 ± 500 Oui 20 ± 300 respectivement. À présent, nous pouvons générer les distributions. Dans cet article, je vais utiliser le langage R. Bien sûr, autres langages de science des données, comme Python, ils peuvent le faire aussi. Voir que les données simulées ont une moyenne et un standard similaires, pas le même, que les paramètres d'entrée.

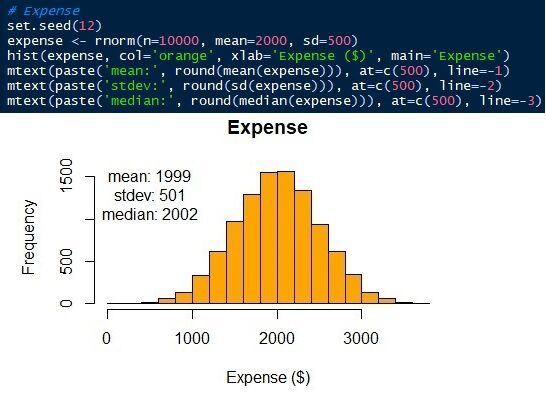
Fig. 6 Répartition normale des frais de subsistance

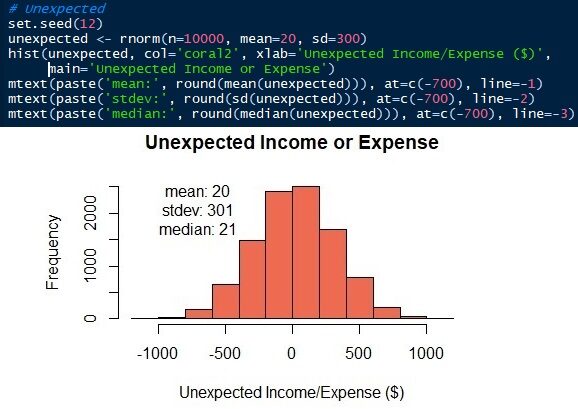
Fig. 7 Répartition normale des revenus ou dépenses imprévus

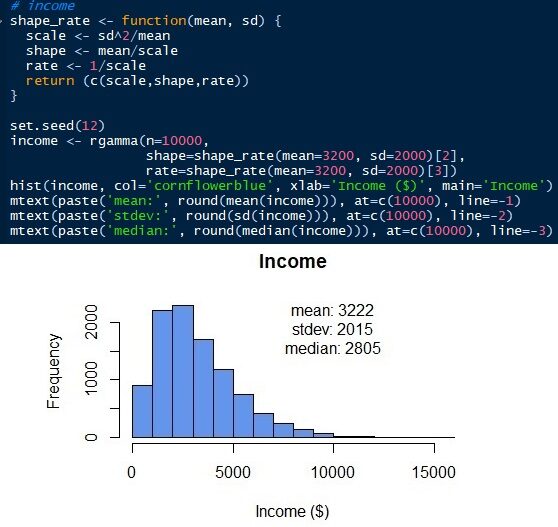
Pour générer la distribution gamma, nous devons connaître d'autres paramètres. Contrairement à la distribution normale, la distribution gamma a une échelle, forme et vitesse comme paramètres. Mais nous pouvons obtenir ces paramètres avec la moyenne et l'écart type (de). Échelle = sd²/vouloir dire. Forme = moyenne / escalader. Taux = 1 / escalader. Alors, nous pouvons simuler la distribution gamma du revenu des employés comme indiqué ci-dessous. La distribution gamma ne peut avoir que des valeurs positives. Il n'y a pas de valeur ci-dessous 0 puisque le revenu de tous les employés doit être un nombre positif. La distribution normale donnerait des valeurs négatives si l'erreur standard est trop grande. Voir que la distribution simulée a une moyenne et un écart type de 3222 Oui 2015 respectivement, qui sont proches des paramètres d'entrée d'origine. Mais nous avons une médiane de 2805. La médiane de la distribution gamma, contrairement à la distribution normale, est loin de la moyenne.

Le crédit à payer mensuellement, comme mentionné précédemment, n'a pas de fonction de densité de probabilité appropriée. Jetez un œil aux réponses de 50 enquêtes en Figure 9 (histogramme gris). Il semble que la plupart des gens doivent rembourser leur crédit de $ 100 Oui $ 300. Pour simuler le 50 observations dans 10,000 observations, on peut utiliser une distribution non paramétrique. Comme son nom l'indique, la distribution non paramétrique ne nécessite aucun paramètre, en moyenne, l'écart type, la forme ou le taux, comme le font les distributions normale et gamma. Nécessite uniquement les données d'origine.

La dernière variable à simuler est le taux d'intérêt bancaire. Le taux d'intérêt bancaire varie de 0,3 une 1,5 uniformément. Faisons de même 10,000 des observations allant de 0.3 une 1.5 avec la même probabilité.

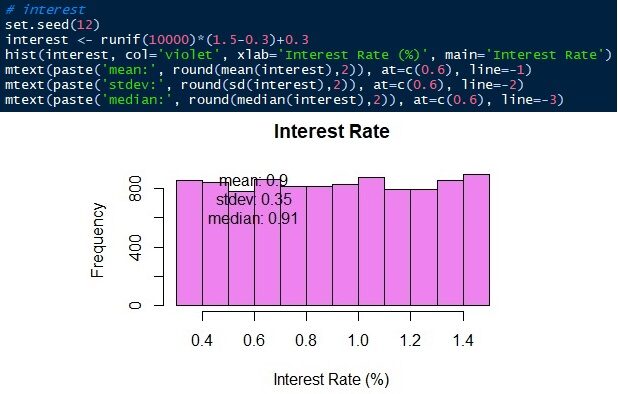
3. Combinaison de simulations Monte Carlo

La dernière étape consiste à combiner les simulations de Monte Carlo en utilisant l'équation pour calculer les économies mensuelles. Pour faire ceci, nous avons juste besoin de rassembler toutes les simulations dans un seul tableau. Alors, on peut calculer 10,000 lignes d'épargne mensuelle. Le résultat est $ 1073 ± 2052, pas très différent de la propagation de l'erreur. Mais, La simulation Monte Carlo montre la densité de probabilité. Nous pouvons voir que l'épargne médiane est $ 666 et les données vont de $ 2000 Oui 10000.

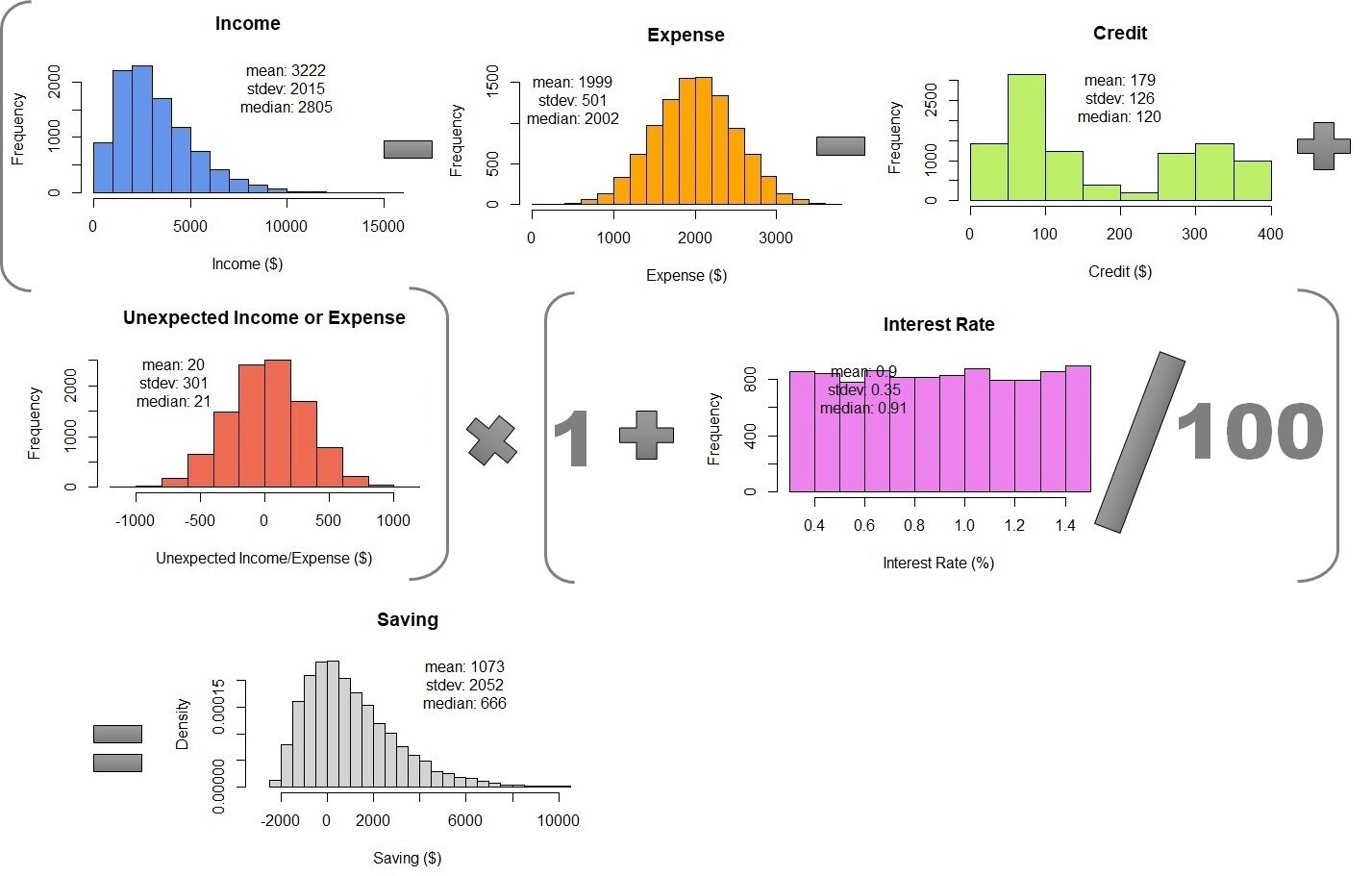
Tableau 1 – Combinaison de simulations Monte Carlo

À présent, regardons un autre exemple avec la variabilité spatiale et temporelle. La tâche consiste à calculer le ruissellement superficiel d'un bassin. Le bassin est la limite de l'hydrologie des eaux de surface. Toute la pluie qui tombe en dessous du bassin ne franchira pas la limite. Une partie de la pluie s'infiltre dans le sol selon la taille des particules de sol et le type d'occupation du sol. L'eau qui ne s'infiltre pas dans le sol est appelée ruissellement de surface. Le ruissellement de surface s'écoulera dans la rivière sous forme de débit de la rivière.

Le tableau suivant montre l'intensité des précipitations mensuelles dans une année et le coefficient de ruissellement dans une 1,5 km.² cuenca. L'incertitude peut être due à l'hétérogénéité spatiale et temporelle. Le coefficient de précipitation et de ruissellement (en raison du type de sol et de couverture terrestre) varie spatialement dans le bassin. Les précipitations du bassin sont mesurées avec divers pluviomètres. Ils donnent des précipitations moyennes avec une incertitude due à la distribution spatiale. La distribution de l'occupation du sol donne également l'incertitude du coefficient de ruissellement.

Un coefficient de ruissellement est la proportion de pluie qui ne s'infiltre pas dans le sol et devient un ruissellement de surface. Le type de forêt ou de sol épais a un faible coefficient de ruissellement. Les agglomérations ou les maisons ont un coefficient de ruissellement élevé. La conversion de la couverture forestière en peuplements augmente le coefficient de ruissellement car une proportion plus élevée des eaux de pluie sera le ruissellement de surface.

La variabilité temporelle se produit également parce que les pluies des saisons humides et sèches sont différentes.. L'évolution de l'occupation des sols au cours du temps entraîne également la variabilité temporelle du coefficient de ruissellement. D'autres sources d'incertitude sont la qualité des outils de mesure, méthodes de mesure, conditions environnementales et autres conditions inexpliquées dues au manque de connaissances.

Mes	Précipitations (mm / mes)	Coefficient de ruissellement	Zone (km2)
une	320 ± 37	0,3 ± 0,2	1,5
fév	350 ± 59	0,3 ± 0,2	1,5
Mar	205 ± 26	0,4 ± 0,1	1,5
avr	170 ± 41	0,4 ± 0,1	1,5
Mayo	106 ± 48	0,4 ± 0,1	1,5
juin	91 ± 32	0,4 ± 0,1	1,5
juil	77 ± 16	0,4 ± 0,1	1,5
depuis	52 ± 15	0,7 ± 0,2	1,5
SEP	100 ± 50	0,7 ± 0,2	1,5
oct	120 ± 46	0,7 ± 0,2	1,5
nov	253 ± 45	0,7 ± 0,2	1,5
déc	210 ± 48	0,7 ± 0,2	1,5

L'équation est ruissellement de surface = intensité des précipitations × coefficient de ruissellement × superficie du bassin. L'ensemble de la distribution est simulé à l'aide d'une distribution gamma. Le ruissellement de surface mensuel moyen est 124.000 ± 30 m³/mes. La médiane est 120.000 m³/mes.

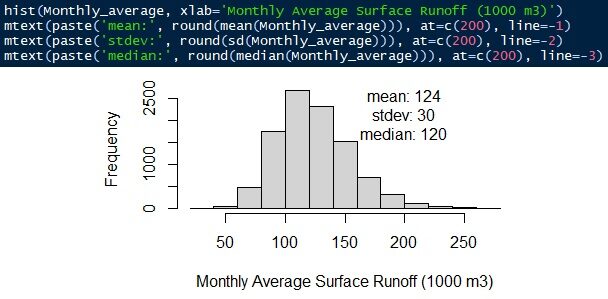
Fig. 12 Écoulement de surface mensuel moyen

A propos de l'auteur

Connectez-vous avec moi ici https://www.linkedin.com/in/rendy-kurnia/

En rapport