introduzione:
In questo articolo, impareremo tutti i concetti statistici importanti richiesti per i ruoli di data science.
Sommario:
- Differenza tra parametro e statistica
- Statistiche e loro tipi
- Tipi di dati e livelli di misurazione
- Momenti di decisione aziendale
- Teorema del limite centrale (CLT)
- Distribuzioni di probabilità
- Rappresentazioni grafiche
- Verifica di ipotesi
1. Differenza tra parametro e statistica
Nel nostro quotidiano continuiamo a parlare di Popolazione e spettacoli. Quindi, è molto importante conoscere la terminologia per rappresentare la popolazione e il campione.
Un parametro è un numero che descrive i dati della popolazione. E una statistica è un numero che descrive i dati in un campione.
2. Statistiche e loro tipi
La definizione di Wikipedia di Statistica afferma che “è una disciplina che si occupa della compilazione, organizzazione, analisi, interpretazione e presentazione dei dati”.
Significa che, come parte dell'analisi statistica, noi raccogliamo, organizzare ed estrarre informazioni significative dai dati, tramite visualizzazioni o spiegazioni matematiche.
Le statistiche sono generalmente classificate in due tipi:
- Statistiche descrittive
- Statistica inferenziale
Statistiche descrittive:
Come suggerisce il nome in Statistiche descrittive, Descriviamo i dati utilizzando le distribuzioni medie, Deviazione standard, Grafici o probabilità.
Fondamentalmente, come parte delle statistiche descrittive, misuriamo quanto segue:
- Frequenza: no. numero di volte in cui si verifica un punto dati
- Tendenza centrale: la centralità dei dati: media, medianoLa mediana è una misura statistica che rappresenta il valore centrale di un insieme di dati ordinati. Per calcolarlo, I dati sono organizzati dal più basso al più alto e viene identificato il numero al centro. Se c'è un numero pari di osservazioni, I due valori fondamentali sono mediati. Questo indicatore è particolarmente utile nelle distribuzioni asimmetriche, poiché non è influenzato da valori estremi.... e moda.
- Dispersione: la portata dei dati: classifica, varianza e deviazione standard
- Il misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... della posizione: percentili e intervalli di quantili
Statistica inferenziale:
In Statistica Inferenziale, Stimiamo il parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... popolazione. Oppure eseguiamo test di ipotesi per valutare le ipotesi fatte sui parametri della popolazione..
In parole povere, interpretiamo il significato delle statistiche descrittive deducendole alla popolazione.
Ad esempio, stiamo conducendo un'indagine sul numero di veicoli a due ruote in una città. Supponiamo che la città abbia una popolazione totale di 5L persone. Perciò, abbiamo preso un campione di 1000 persone, in quanto è impossibile eseguire un'analisi dei dati dell'intera popolazione.
Dal sondaggio effettuato, si trova che 800 persone da 1000 (800 a partire dal 1000 è 80%) sono due ruote. Quindi, possiamo dedurre questi risultati alla popolazione e concludere che le persone 4L della popolazione 5L sono due ruote.
3. Tipi di dati e livello di misurazione
A un livello superiore, i dati sono classificati in due tipi: Qualitativo e Quantitativo.
I dati qualitativi non sono numerici. Alcuni degli esempi sono il colore degli occhi, marca di automobili, la città, eccetera.
In secondo luogo, i dati quantitativi sono numerici e di nuovo suddivisi in dati continui e discreti.
Dati continui: Può essere rappresentato in formato decimale. Alcuni esempi sono l'altezza, il peso, tempo metereologico, distanza, eccetera.
Dati discreti: Non può essere rappresentato in formato decimale. Alcuni esempi sono il numero di laptop, il numero di studenti in una classe.
I dati discreti vengono suddivisi in dati categorici e di conteggio.
Dati categoriali: rappresentano il tipo di dati che possono essere suddivisi in gruppi. Alcuni esempi sono l'età, sesso, eccetera.
Contare i dati: Questi dati contengono numeri interi non negativi. Esempio: numero di figli che un partner ha.
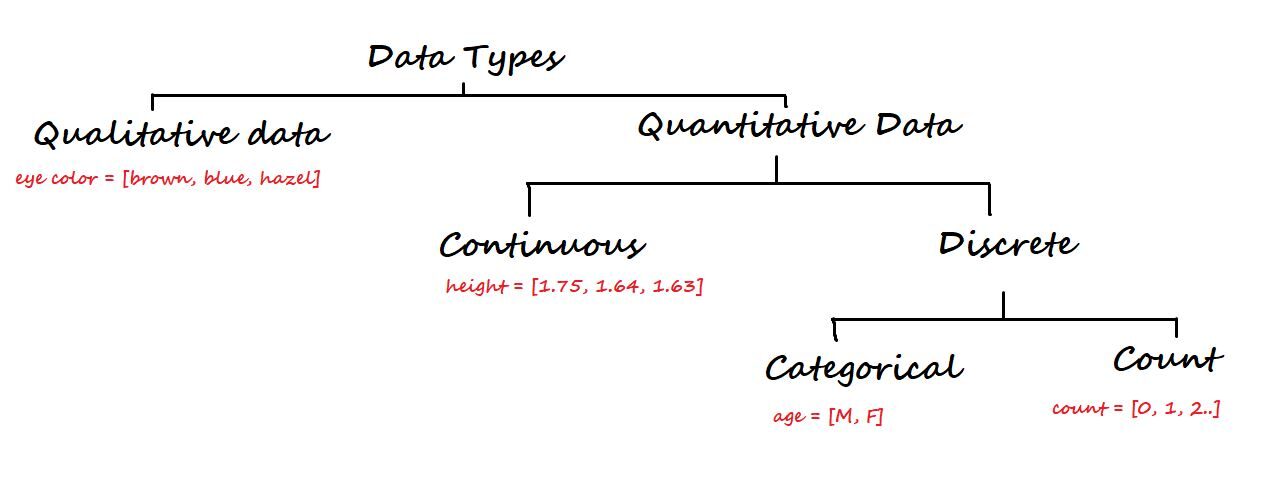
Livello di misurazione
Nelle statistiche, Il livello di misurazione è una classificazione che descrive la relazione tra i valori di un variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.....
Abbiamo quattro livelli fondamentali di misurazione. Figlio:
- Scala nominale
- Scala ordinale
- Scala dell'intervallo
- Scala delle proporzioni
1. Scala nominale: Questa scala contiene la minor quantità di informazioni poiché i dati hanno solo nomi / etichette. Può essere utilizzato per la classificazione. Non possiamo eseguire operazioni matematiche su dati nominali perché non esiste un valore numerico per le opzioni (i numeri associati ai nomi possono essere usati solo come etichette).
Esempio: A quale paese appartieni? India, Giappone, Corea.
2. Scala ordinale: Rispetto alla scala nominale, la scala ordinale ha più informazioni perché insieme alle etichette, ha ordine / indirizzo.
Esempio: Livello di reddito: alto reddito, reddito medio, Bassi introiti.
3. Scala dell'intervallo: È una scala numerica. La scala degli intervalli ha più informazioni rispetto alle scale ordinali nominali. Insieme all'ordine, conosciamo la differenza tra le due variabili (l'intervallo indica la distanza tra due entità).
La media può essere utilizzata, la mediana e la modalità per descrivere i dati.
Esempio: temperatura, reddito, eccetera.
4. Scala del rapporto: La scala dei rapporti contiene la maggior parte delle informazioni sui dati. A differenza delle altre tre scale, la scala del rapporto può ospitare un vero punto zero. Si dice semplicemente che la scala dei rapporti è la combinazione delle scale Nominale, Ordinale e Intercal.
Esempio: peso attuale, altezza, eccetera.
4. Momenti di decisione aziendale
Abbiamo quattro momenti decisionali aziendali che ci aiutano a comprendere i dati.
4.1. Misure di tendenza centrale
(Conosciuta anche come decisione aziendale in primo luogo)
Parliamo della centralità dei dati. per semplificarlo, fa parte dell'analisi statistica descrittiva in cui un singolo valore al centro rappresenta l'intero set di dati.
La tendenza centrale di un insieme di dati può essere misurata da:
per significare: È la somma di tutti i punti dati divisa per il numero totale di valori nel set di dati. Non ci si può sempre fidare della media perché è influenzata da valori anomali.
Mediano: È il valore intermedio di un insieme di dati ordinato / ordinato. Se la dimensione del set di dati è pari, la mediana si calcola facendo la media dei due valori medi.
Modo: È il valore più ripetuto nel set di dati. I dati con una sola modalità sono chiamati unimodal, i dati con due modalità sono chiamati bimodali e i dati con più di due modalità sono chiamati multimodali.
4.2. Misure di dispersione
(Conosciuto anche come decisione aziendale per la seconda volta)
Parla della diffusione dei dati dal tuo centro.
La dispersione può essere misurata usando:
Differenza: È la distanza quadratica media di tutti i punti dati dalla sua media. Il problema con la varianza è che anche le unità saranno quadrate.
Deviazione standard: È la radice quadrata della varianza. Aiuta a recuperare le unità originali.
Distanza: È la differenza tra i valori massimo e minimo di un set di dati.
Misurare | Popolazione | Spettacoli |
| per significare | µ = (Xio)/NORD | x̄ = (xio)/Nord |
| Mediano | Il valore medio dei dati | Il valore medio dei dati |
| Modo | Valore più verificato | Valore più verificato |
| Differenza | ?2 = (Xio – µ)2/NORD | S2 = (xio – X )2/ (n-1) |
| Deviazione standard | σ = radice quadrata ((Xio – µ)2/NORD) | s = radice quadrata ((xio – X )2/ (n-1)) |
| Distanza | Massimo minimo | Massimo minimo |
4.3. Obliquità
(È anche conosciuta come una decisione aziendale nel terzo momento)
Misura l'asimmetria dei dati. I due tipi di asimmetria sono:
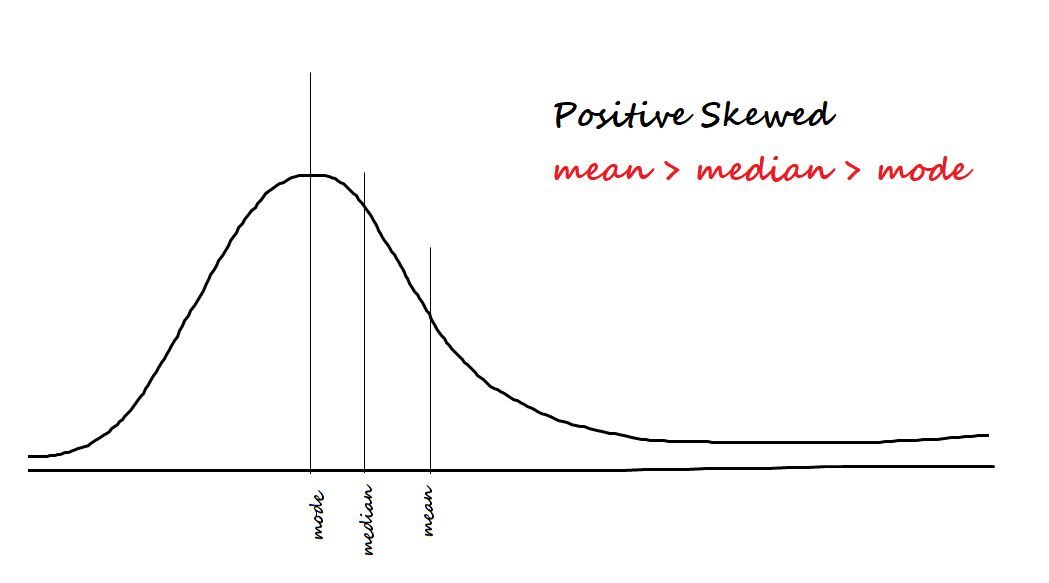
Positivo / inclinato a destra: Si dice che i dati siano distorti positivamente se la maggior parte dei dati è concentrata sul lato sinistro e ha una coda a destra.
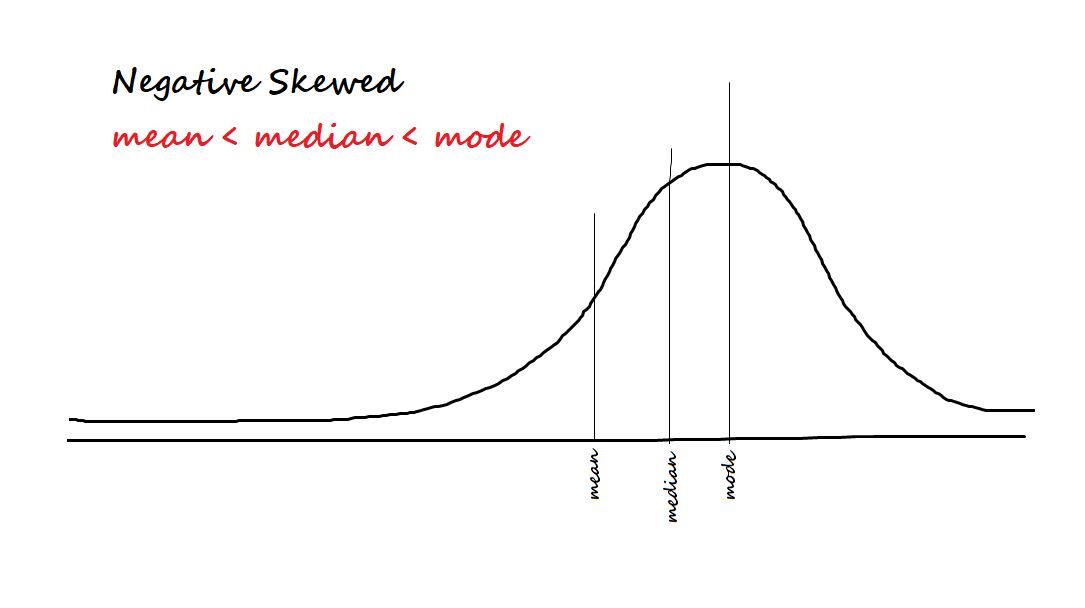
Negativo / inclinato a sinistra: Si dice che i dati siano distorti negativamente se la maggior parte dei dati è concentrata sul lato destro e ha una coda a sinistra.
La formula dell'asimmetria è me [(X - µ)/ ? ]) 3 = Z3
4.4. curtosi
(Conosciuto anche come decisione aziendale del quarto momento)
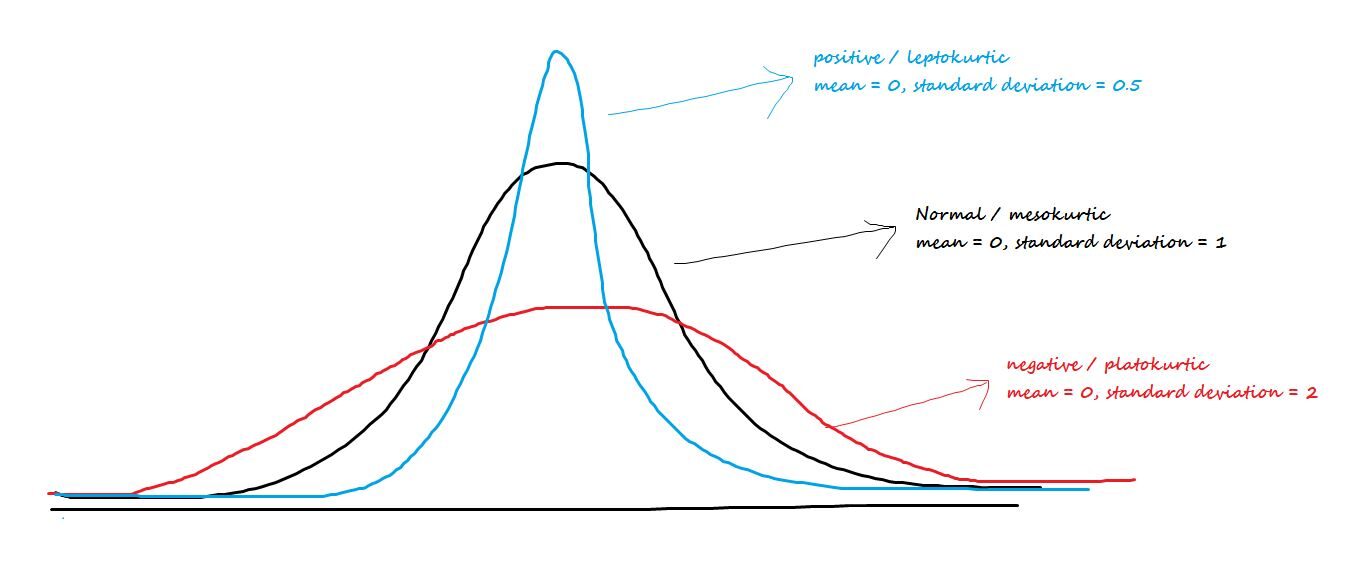
Parla del picco centrale o della rotondità delle code. I tre tipi di curtosi sono:
Positivo / leptocurtico: Ha becchi affilati e code più leggere.
Negativo / Platokúrtico: Ha becchi larghi e code più spesse.
mesokurtico: Distribuzione normale
La formula della curtosi è me [(X - µ)/ ? ]) 4-3 = Z4– 3
Insieme, l'asimmetria e la curtosi sono chiamate statistiche di forma.
5. Teorema del limite centrale (CLT)
Invece di analizzare i dati dell'intera popolazione, prendiamo sempre un campione per l'analisi. Il problema con il campionamento è che "la media campionaria è una variabile casuale, varia per diversi campioni ". E il campione casuale che estraiamo non può mai essere una rappresentazione esatta della popolazione. Questo fenomeno è chiamato variazione campionaria.
Per annullare la variazione del campione, usiamo il teorema del limite centrale. E secondo il teorema del limite centrale:
1. La distribuzione della media campionaria segue una distribuzione normale se la popolazione è normale.
2. la distribuzione della media campionaria segue una distribuzione normale anche se la popolazione non è normale. Ma la dimensione del campione dovrebbe essere abbastanza grande.
3. La grande media di tutti i valori medi campionari ci dà la media della popolazione.
4. Teoricamente, la dimensione del campione dovrebbe essere 30. E praticamente, la condizione sulla dimensione del campione (n) è:
n> 10 (K3)2, dove k3 è l'asimmetria del campione.
n> 10 (K4), dove K4 è il campione di curtosi.
6. Distribuzioni di probabilità
In termini statistici, una funzione di distribuzione è un'espressione matematica che descrive la probabilità di diversi possibili risultati per un esperimento.
Per favore, leggi questo mio articolo sui diversi tipi di distribuzioni di probabilità.
7. Rappresentazioni grafiche
La rappresentazione grafica si riferisce all'uso di tabelle o grafici per visualizzare, analizzare e interpretare i dati numerici.
Per una singola variabile (analisi invariate), abbiamo un grafico a barre, un diagramma a linee, un diagramma di frequenza, una trama a punti, un box plot e il normale QQ plot.
Discuteremo il box plot e il normale QQ plot.
7.1. Trama scatola
Un box plot è un modo per visualizzare la distribuzione dei dati in base a un riepilogo di cinque numeri. Utilizzato per identificare valori anomali nei dati.
I cinque numeri sono minimi, primo quartile (Q1), mediano (Q2), terzo quartile (Q3) e massimo.
La regione della casella conterrà il 50% dei dati. Il 25% la parte inferiore dell'area dati è chiamata Bottom Whisker e la parte inferiore 25% la parte superiore dell'area dati si chiama Top Whisker.
La regione interquartile (IQR) è la differenza tra il terzo e il primo quartile. IQR = Q3 – Q1.
Gli outlier sono i punti dati sotto il baffo inferiore e oltre il baffo superiore.
La formula per trovare gli outlier è Valore anomalo = Q ± 1,5 * (IQR)
I valori anomali sotto il baffo inferiore sono dati come Q1 – 1,5 * (IQR)
I valori anomali oltre il baffo superiore sono dati come Q3 + 1.5 * (IQR)
Vedi il mio articolo sul rilevamento degli outlier usando un box plot.
7.2. Grafico QQ normale
Un normale diagramma QQ è una sorta di Diagramma di dispersioneIl grafico a dispersione è uno strumento grafico utilizzato in statistica per visualizzare la relazione tra due variabili. Consiste in un insieme di punti in un piano cartesiano, dove ogni punto rappresenta una coppia di valori corrispondenti alle variabili analizzate. Questo tipo di grafico consente di identificare i modelli, Tendenze e possibili correlazioni, facilitare l'interpretazione dei dati e il processo decisionale sulla base delle informazioni visive presentate.... che viene tracciato creando due insiemi di quantili. Viene utilizzato per verificare se i dati sono normali o meno.
Sull'asse x abbiamo i punteggi Z e sull'asse y abbiamo i quantili del campione effettivo. Se il grafico a dispersione forma una linea retta, si dice che i dati siano normali.
8. Verifica di ipotesi
Il test di ipotesi nelle statistiche è un modo per testare le ipotesi fatte sui parametri della popolazione.
Vedi il mio articolo sui test di ipotesi per leggerlo in dettaglio.
Note finali:
Grazie per aver letto fino alla conclusione. Alla fine di questo articolo, conosciamo importanti concetti statistici.
Spero che questo articolo sia informativo. Sentiti libero di condividerlo con i tuoi compagni studenti.
Altri miei post sul blog
Sentiti libero di dare un'occhiata agli altri post del mio blog dal mio profilo DataPeaker.
Mi puoi trovare in LinkedIn, Twitter nel caso volessi connetterti. Mi piacerebbe connettermi con te.
Per un immediato scambio di opinioni, Scrivimi [e-mail protetta].
Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.
