Algoritmo di regressione lineare per una facile previsione

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati

introduzione

. Un problema de regresión es cuando la variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... de salida es un valor real o continuo.

In regressione, tracciamo un grafico tra le variabili che meglio si adattano ai punti dati dati. Il modello di apprendimento automatico può fornire previsioni sui dati. Ecco alcuni consigli gratuiti!, “La regressione mostra una linea o una curva che passa attraverso tutti i punti dati su un grafico di previsione target in modo tale che la distanza verticale tra i punti dati e la linea di regressione sia minima”. Viene utilizzato principalmente per prevedere, prevedere, modellare le serie temporali e determinare la relazione causale-effetto tra le variabili.

Tipi di modelli di regressione

1. Regressione lineare
2. Regressione polinomiale
3. Regressione logistica

Regressione lineare

La regressione lineare è un metodo di regressione statistica semplice e silenzioso utilizzato per l'analisi predittiva e mostra la relazione tra variabili continue. La regressione lineare mostra la relazione lineare tra la variabile indipendente (asse X) e la variabile dipendente (asse y), di conseguenza chiamato regressione lineare. Se c'è una singola variabile di input (X), detta regressione lineare si chiama Regressione lineare semplice. E se c'è più di una variabile di input, detta regressione lineare si chiama regressione lineare multipla. Il modello di regressione lineare fornisce una linea retta inclinata che descrive la relazione all'interno delle variabili.

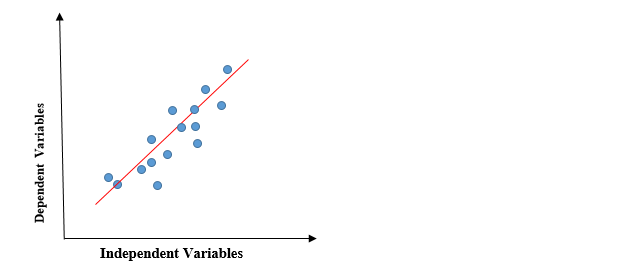
Il grafico precedente presenta la relazione lineare tra la variabile dipendente e le variabili indipendenti. Quando il valore di x (variabile indipendente) aumenta, il valore di y (variabile dipendente) sta anche aumentando. La linea rossa è conosciuta come la linea retta di miglior adattamento.. Sulla base dei punti dati forniti, cerchiamo di tracciare una linea che modelli meglio i punti.

Per calcolare la regressione lineare della linea di miglior adattamento, viene utilizzata una forma tradizionale di intercettazione pendenza.

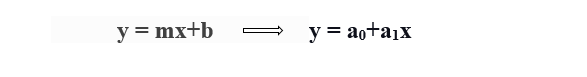
y = variabile dipendente.

x = variabile indipendente.

a0 = intersezione della retta.

a1 = Coefficiente di regressione lineare.

Necessità di una regressione lineare

Come menzionato prima, la regressione lineare stima la relazione tra una variabile dipendente e una variabile indipendente. Capiamolo con un semplice esempio:

Supponiamo di voler stimare lo stipendio di un dipendente in base all'anno di esperienza. Hai i dati recenti dell'azienda, che indica che il rapporto tra esperienza e stipendio. Qui l'anno di esperienza è una variabile indipendente e lo stipendio di un dipendente è una variabile dipendente., poiché lo stipendio di un dipendente dipende dall'esperienza di un dipendente. Con queste informazioni, possiamo prevedere lo stipendio futuro del dipendente in base alle informazioni attuali e passate.

Una linea di regressione può essere una relazione lineare positiva o una relazione lineare negativa.

Relazione lineare positiva

Se la variabile dipendente si espande sull'asse Y e la variabile indipendente avanza sull'asse X, questa relazione è chiamata relazione lineare positiva.

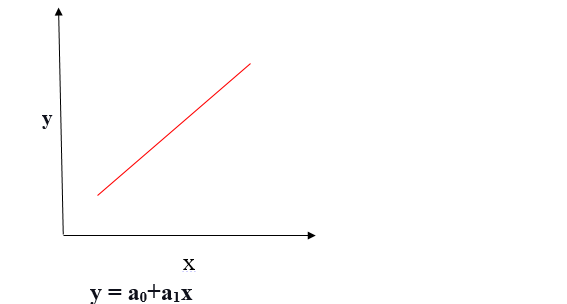
Relazione lineare negativa

Se la variabile dipendente diminuisce sull'asse Y e la variabile indipendente aumenta sull'asse X, questa relazione è chiamata relazione lineare negativa.

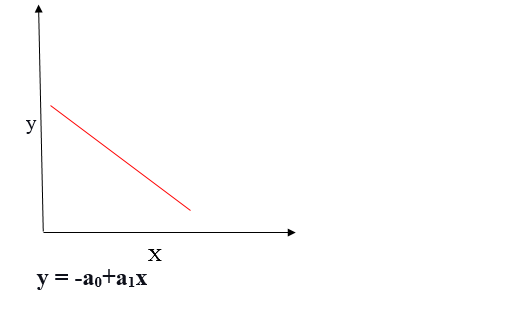
L'obiettivo dell'algoritmo di regressione lineare è ottenere i migliori valori per a0 e a1 per trovare la linea di miglior adattamento. La linea di miglior adattamento dovrebbe avere il minor errore, il che significa che l'errore tra i valori previsti e i valori effettivi dovrebbe essere ridotto al minimo.

Funzione di costo

La funzione di costo aiuta a determinare i migliori valori possibili per a0 e a1, che fornisce la linea di miglior adattamento per i punti dati.

La funzione di costo ottimizza i coefficienti oi pesi di regressione e misura il rendimento di un modello di regressione lineare. La funzione di costo viene utilizzata per trovare la precisione di funzione di mappatura che mappa la variabile di input alla variabile di output. Questa funzione di mappatura è anche nota come la funzione ipotesi.

Nella regressione lineare, Root errore quadratico medio (MSE) Viene utilizzata la funzione di costo, che è la media dell'errore al quadrato che si è verificato tra i valori previsti e i valori effettivi.

Per semplice equazione lineare y = mx + b possiamo calcolare MSE come:

Facciamo y = valori reali, e_io = valori previsti

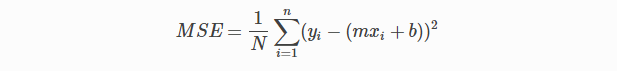
Utilizzo della funzione MSE, cambieremo i valori di a0 e a1 in modo che il valore MSE sia impostato ai minimi. ParametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... del modelo xi, B (un₀,un₁) può essere manipolato per ridurre al minimo la funzione di costo. Questi parametri possono essere determinati utilizzando il metodo della discesa del gradiente in modo che il valore della funzione di costo sia minimo.

Discesa gradiente

La discesa del gradiente è un metodo per aggiornare a0 e a1 per ridurre al minimo la funzione di costo (MSE). Un modello di regressione utilizza la discesa del gradiente per aggiornare i coefficienti della linea (a0, a1 => xi, B) riducendo la funzione di costo utilizzando una selezione casuale di valori dei coefficienti e quindi aggiornando iterativamente i valori per raggiungere la funzione di costo minimo.

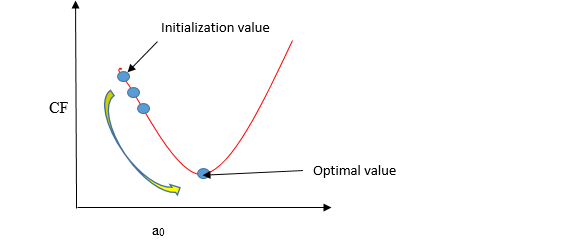
Immagina un pozzo a forma di U. Ti trovi nel punto più alto del pozzo e il tuo obiettivo è raggiungere il fondo del pozzo. C'è un tesoro, e puoi fare solo un discreto numero di passaggi per arrivare in fondo. Se decidi di fare un passo alla volta, alla fine raggiungerai il fondo del pozzo, ma questo richiederà più tempo. Se scegli di fare passi più lunghi ogni volta, può arrivare prima, ma c'è la possibilità che vada oltre il fondo del pozzo e non vicino al fondo. Nell'algoritmo di discesa del gradiente, il numero di passi che fai è il tasso di apprendimento, e questo decide quanto velocemente l'algoritmo converge ai minimi.

Per aggiornare un₀ e un₁, prendiamo gradienti dalla funzione di costo. Per trovare questi gradienti, prendiamo derivate parziali per a₀ e un₁.

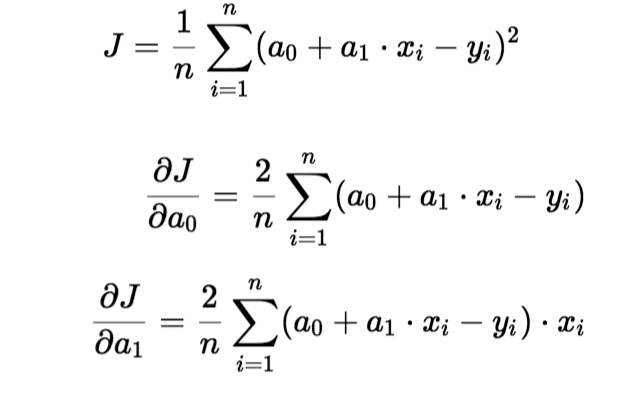
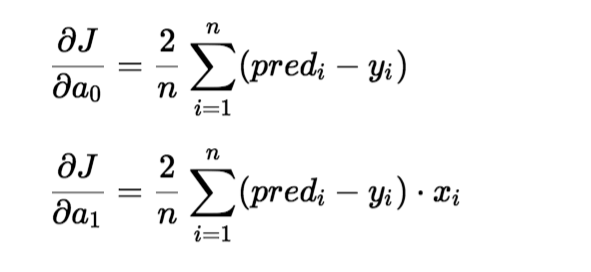
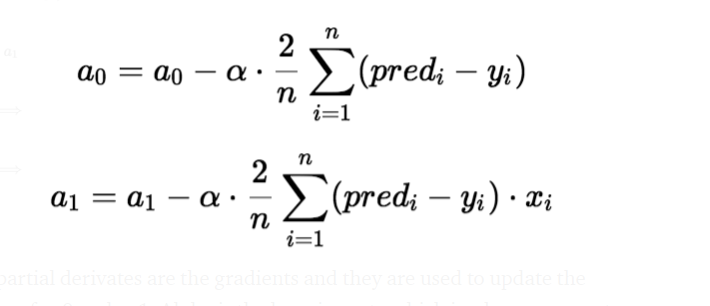
Le derivate parziali sono i gradienti e servono per aggiornare i valori di a₀ e un₁. Alpha è il tasso di apprendimento.

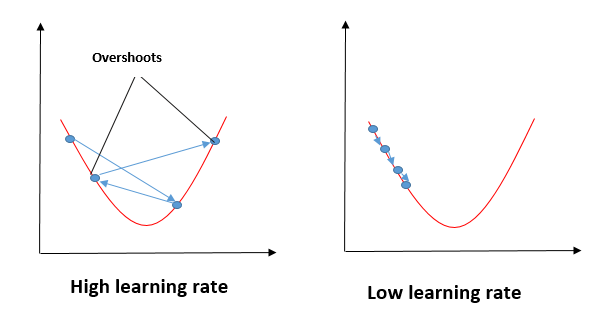
Impatto di diversi valori per il tasso di apprendimento

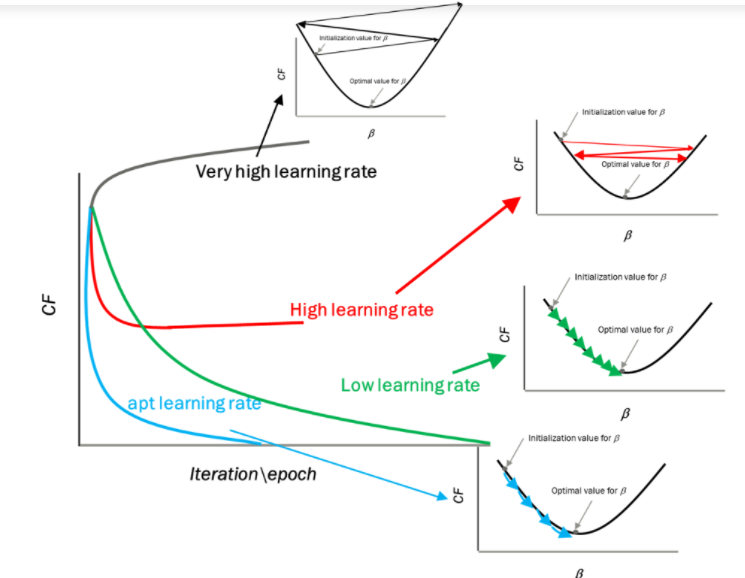
Fonte: mygreatleaning.com

La linea blu rappresenta il valore ottimale del tasso di apprendimento e il valore della funzione di costo viene minimizzato in poche iterazioni. La linea verde rappresenta se il tasso di apprendimento è inferiore al valore ottimale, allora il numero di iterazioni richieste è alto per minimizzare la funzione di costo. Se il tasso di apprendimento selezionato è molto alto, la funzione di costo potrebbe continuare ad aumentare con le iterazioni e saturare fino a un valore superiore al valore minimo, quello rappresentato da una linea rossa e nera.

Caso d'uso

In questo, Prenderò numeri casuali per la variabile dipendente (stipendio) e una variabile indipendente (Esperienza) e prevedo l'impatto di un anno di esperienza sullo stipendio.

Passi per implementare il modello di regressione lineare

importa alcune librerie richieste

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

Definire il set di dati

x= np.array([2.4,5.0,1.5,3.8,8.7,3.6,1.2,8.1,2.5,5,1.6,1.6,2.4,3.9,5.4])
y = np.array([2.1,4.7,1.7,3.6,8.7,3.2,1.0,8.0,2.4,6,1.1,1.3,2.4,3.9,4.8])
n = np.size(X)

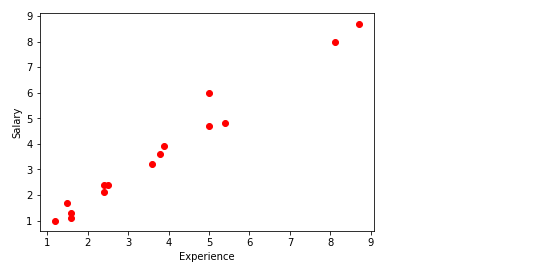
Tracciare i punti dati

plt.scatter(esperienza,stipendio, colore="rosso")
plt.xlabel("Esperienza")
plt.ylabel("Stipendio")
plt.mostra()

La funzione principale per il calcolo dei valori dei coefficienti.

1. Inizializzare i parametri.
2. Prevedere il valore di una variabile dipendente data una variabile indipendente.
3. Calcolare l'errore nella previsione per tutti i punti dati.
4. Calcola la derivata parziale wrt a0 e a1.
5. Calcola il costo di ogni numero e sommali.
6. Aggiornare i valori di a0 e a1.

#initialize the parameters
a0 = 0                  #intercept
a1 = 0                  #Slop
lr = 0.0001             #Learning rate
iterations = 1000       # Number of iterations
error = []              # Matrice di errore per calcolare il costo per ogni iterazione.
per itr nell'intervallo(Iterazioni):
    error_cost = 0
    cost_a0 = 0
    cost_a1 = 0
    per io nel raggio d'azione(len(esperienza)):
        y_pred = a0+a1*esperienza[io]   # predict value for given x
        error_cost = error_cost +(stipendio[io]-y_pred)**2
        per j nell'intervallo(len(esperienza)):
            partial_wrt_a0 = -2 *(stipendio[J] - (a0 + a1*esperienza[J]))                #partial derivative w.r.t a0
            partial_wrt_a1 = (-2*esperienza[J])*(stipendio[J]-(a0 + a1*esperienza[J]))   #partial derivative w.r.t a1
            cost_a0 = cost_a0 + partial_wrt_a0      #calculate cost for each number and add
            cost_a1 = cost_a1 + partial_wrt_a1      #calculate cost for each number and add
        a0 = a0 - lr * cost_a0    #update a0
        a1 = a1 - lr * cost_a1    #update a1
        print(itr,a0,a1)          #Check iteration and updated a0 and a1
    error.append(error_cost)      #Aggiungere i dati nella matrice

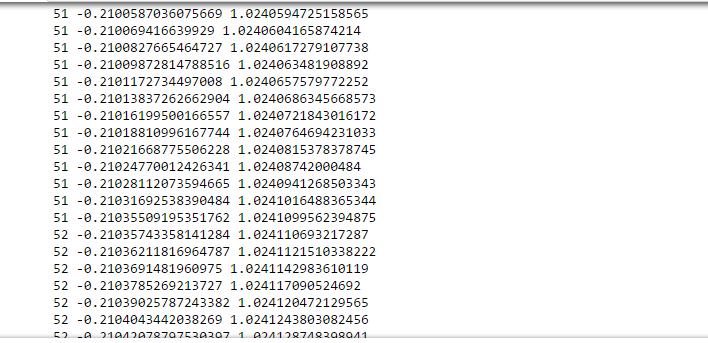
En una iteración aproximada de 50-60, obtuvimos el valor de a0 y a1.

Stampa(a0)
Stampa(a1)

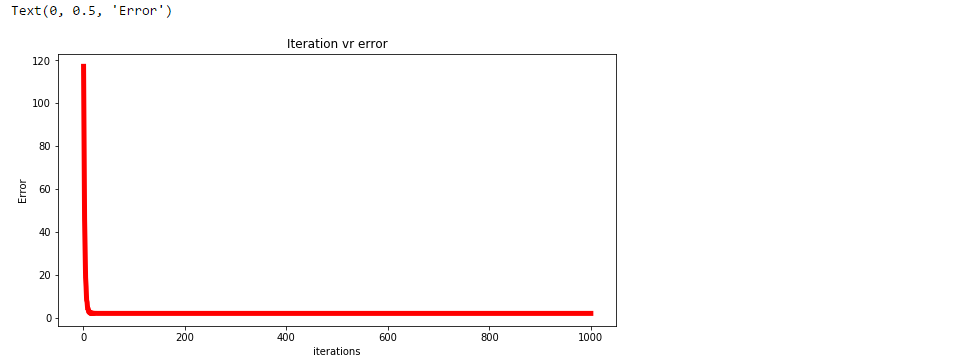
Trazar el error para cada iteración.

plt.figure(figsize=(10,5))
plt.trama(np.arange(1,len(errore)+1),errore,colore="rosso",larghezza di riga = 5)
plt.titolo("Errore vr di iterazione")
plt.xlabel("Iterazioni")
plt.ylabel("Errore")

Prevedere i valori.

pred = a0+a1*experience
print(pred)

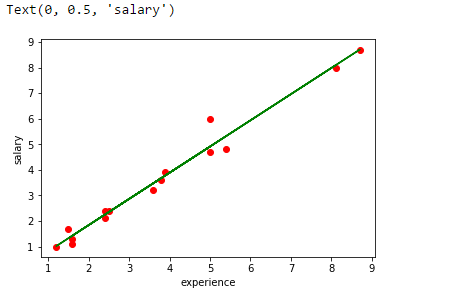
Tracciare la linea di regressione.

plt.scatter(esperienza,stipendio,colore="rosso")
plt.trama(esperienza,pred, colore="verde")
plt.xlabel("esperienza")
plt.ylabel("stipendio")

Analizzare le prestazioni del modello calcolando l'errore quadrato medio.

errore1 = stipendio - pred
se = np.sum(errore1 ** 2)
mse = se/n
print("L'errore quadrato medio è", mse)

Utilizzare la libreria scikit per confermare i passaggi precedenti.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error 
experience = experience.reshape(-1,1)
modello = regressione lineare()
model.fit(esperienza,stipendio)
salary_pred = model.predict(esperienza)
Mse = mean_squared_error(stipendio, salary_pred)
Stampa('slop', model.coef_)
Stampa("Intercettare", model.intercept_)
Stampa("MSE", Mse)

Riepilogo

In regressione, tracciamo un grafico tra le variabili che meglio si adattano ai punti dati dati. La regressione lineare mostra la relazione lineare tra la variabile indipendente (asse X) e la variabile dipendente (asse y).Per calcolare la regressione lineare della linea di miglior adattamento, viene utilizzata una forma tradizionale di intercettazione pendenza. Una linea di regressione può essere una relazione lineare positiva o una relazione lineare negativa.

L'obiettivo dell'algoritmo di regressione lineare è quello di ottenere i valori migliori per a0 e a1 per trovare la linea di adattamento migliore e la linea di adattamento migliore dovrebbe avere il minimo errore.. Nella regressione lineare, Root errore quadratico medio (MSE) viene utilizzata la funzione di costo, Quello aiuta a determinare i migliori valori possibili per a0 e a1, che fornisce la linea di miglior adattamento per i punti dati. Utilizzo della funzione MSE, cambieremo i valori di a0 e a1 in modo che il valore MSE sia impostato ai minimi. La discesa del gradiente è un metodo per aggiornare a0 e a1 per ridurre al minimo la funzione di costo (MSE)

Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato