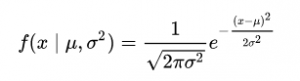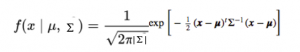Algoritmo di massimizzazione delle aspettative | Spiegazione dell'algoritmo EM

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati

introduzione

sono osservabili. Poiché non abbiamo i valori per le variabili non osservate (latente), il Aspettativa-Massimizzazione L'algoritmo tenta di utilizzare i dati esistenti per determinare i valori ottimali per queste variabili e quindi trova il parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... del modello.

Sommario

• ? Qual è l'algoritmo di massimizzazione delle aspettative? (IN)?
• ? Spiegazione dettagliata dell'algoritmo EM
• ? Diagramma di flusso
• 👉 Vantaggi e svantaggi
• 👉 Applicazioni dell'algoritmo EM
• Caso d'uso dell'algoritmo EM
  • Introduzione alle distribuzioni gaussiane
  • Modelli di miscela gaussiana (GMM)
• 👉 Implementazione di modelli misti gaussiani in Python

Qual è l'algoritmo di massimizzazione delle aspettative? (IN)?

👉 È un modello di variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... latente.

Primo, Capiamo cosa si intende per modello a variabile latente.

Un modello a variabile latente è costituito da osservabile variabili insieme a inosservabile variabili. Le variabili osservate sono quelle variabili nel set di dati che possono essere misurate, mentre le variabili non osservate (latente / nascosto) sono dedotte dalle variabili osservate.

• 👉 Può essere usato per trovare massima verosimiglianza locale (MLE) parametri o massimo a posteriori (CARTA GEOGRAFICA) parametri per variabili latenti
  in un modello statistico o matematico.
• 👉 Utilizzato per prevedere questi valori mancanti nel set di dati, purché si conosca la forma generale della distribuzione di probabilità associata a queste variabili latenti.
• 👉 In parole semplici, l'idea alla base di questo algoritmo è quella di utilizzare i campioni osservabili delle variabili latenti per prevedere i valori dei campioni che non sono osservabili per l'apprendimento. Questo processo viene ripetuto fino a quando non si verifica la convergenza dei valori.

Spiegazione dettagliata dell'algoritmo EM

? Ecco l'algoritmo che devi seguire:

• Dato un set di dati incompleto, iniziare con una serie di parametri inizializzati.
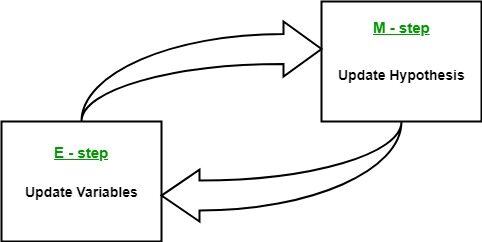
• Aspettativa passo (passo E): In questo passo di attesa, utilizzando i dati osservati disponibili dal set di dati, possiamo provare a stimare o indovinare i valori dei dati mancanti. Finalmente, dopo questo passaggio, otteniamo dati completi senza valori mancanti.
• Fase di massimizzazione (passo M): Ora, dobbiamo usare i dati completi, che si preparano nel passo dell'aspettativa, e aggiorna i parametri.
• Ripetere il passaggio 2 e il passo 3 finché non convergiamo alla nostra soluzione.

Fonte immagine: Collegamento

?

Obiettivo dell'algoritmo di massimizzazione delle aspettative

L'algoritmo di massimizzazione delle aspettative mira a utilizzare i dati osservati disponibili dal set di dati per stimare i dati mancanti per le variabili latenti e quindi utilizzare tali dati per aggiornare i valori dei parametri nella fase di massimizzazione..

Comprendiamo l'algoritmo EM in dettaglio:

• ioFase di inizializzazione: In questo passaggio, inizializziamo i valori dei parametri con un insieme di valori iniziali, quindi consegniamo al sistema il set di dati osservati incompleto con l'assunzione che i dati osservati provengano da un modello specifico. vale a dire, distribuzione di probabilità.
• Aspettativa passo: In questo passaggio, utilizzare i dati osservati per stimare o indovinare valori di dati mancanti o incompleti. Usato per aggiornare le variabili.
• Fase di massimizzazione: In questo passaggio, usiamo i dati completi generati nel “aspettativa” passaggio per aggiornare i valori dei parametri, vale a dire, aggiornare ipotesi.
• Verifica della convergenza Passaggio: Ora, in questo passaggio, controlliamo se i valori stanno convergendo o no, se è così, Fermare, altrimenti ripeti questi due passaggi, vale a dire, il “aspettativa” passo e “Massimizzazione” passo fino a quando non si verifica la convergenza.

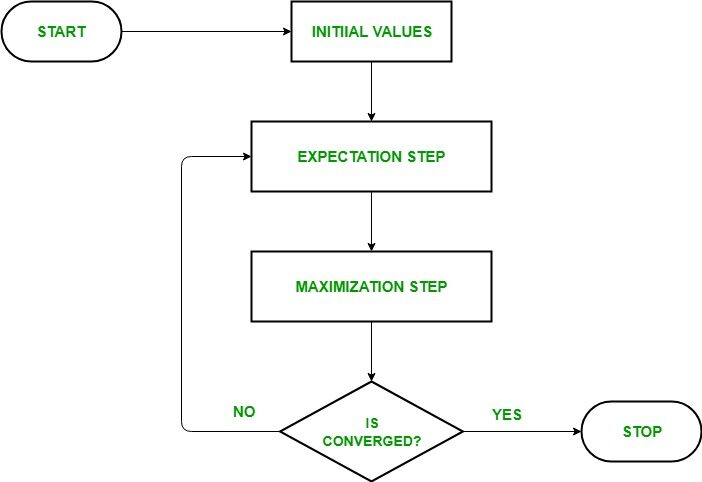
Diagramma di flusso per l'algoritmo EM

Fonte immagine: Collegamento

Vantaggi e svantaggi dell'algoritmo EM

? Vantaggio

• I due passaggi fondamentali dell'algoritmo EM, vale a dire, E-step y M-step, di solito sono abbastanza facili per molti problemi di apprendimento automatico in termini di implementazione.
• La soluzione ai passaggi M spesso esiste in forma chiusa.
• Il valore di probabilità è sempre garantito per aumentare dopo ogni iterazione.

? Svantaggi

• Ho convergenza lenta.
• Convergenza al ottimo locale soltanto.
• Tiene conto sia delle probabilità in avanti che all'indietro. Questo è in contrasto con l'ottimizzazione numerica che considera solo probabilità di anticipo.

Applicazioni dell'algoritmo EM

Il modello a variabile latente ha diverse applicazioni nella vita reale nell'apprendimento automatico:

• Utilizzato per calcolare il Densità gaussiana di una funzione.
• 👉 Utile per completare il dati persi durante uno spettacolo.
• 👉 Trova molto uso in diversi domini come Elaborazione del linguaggio naturale (PNL), Visione computerizzata, eccetera.
• 👉 Utilizzato nella ricostruzione di immagini nel campo della Medicina e ingegneria strutturale.
• 👉 Serve per stimare i parametri del Modello di Markov nascosto (HMM) e anche per altri modelli misti come Miscela gaussiana Modellieccetera.
• 👉 Serve per trovare i valori delle variabili latenti.

Caso d'uso dell'algoritmo EM

Nozioni di base sulla distribuzione gaussiana

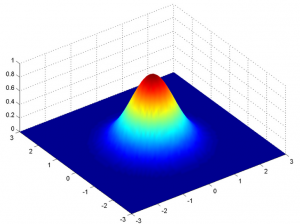
Sono sicuro che hai familiarità con le distribuzioni gaussiane (o la distribuzione normale), poiché questa distribuzione è molto utilizzata nel campo dell'apprendimento automatico e delle statistiche. Ha una curva a campana, con le osservazioni distribuite simmetricamente attorno al valore medio (media).

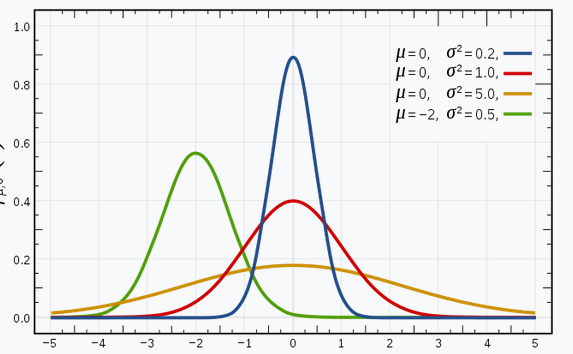
L'immagine mostrata mostra alcune distribuzioni gaussiane con diversi valori della media (μ) e la varianza (?²). Ricorda che maggiore è il valore di (deviazione standard), maggiore è l'estensione lungo l'asse.

Fonte immagine: Collegamento

Nello spazio 1-D, il densità di probabilità di una distribuzione gaussiana è data da:

Fig. Densità di probabilità (PDF)

dove μ rappresenta la media e² rappresenta la varianza.

Ma questo sarebbe vero solo per una variabile solo in 1-D. Nel caso di due variabili, avremo una curva a campana 3D invece di una curva a campana 2D come mostrato di seguito:

La funzione di densità di probabilità sarebbe data da:

dove x è il vettore di input, μ è il vettore medio 2-D e è la matrice di covarianza 2 × 2. Possiamo generalizzare la stessa cosa per il dimensione"Dimensione" È un termine che viene utilizzato in varie discipline, come la fisica, Matematica e filosofia. Si riferisce alla misura in cui un oggetto o un fenomeno può essere analizzato o descritto. In fisica, ad esempio, Si parla di dimensioni spaziali e temporali, mentre in matematica può riferirsi al numero di coordinate necessarie per rappresentare uno spazio. Comprenderlo è fondamentale per lo studio e... D.

Perciò, per il modello gaussiano multivariato, abbiamo x e μ come vettori di lunghezza d, e sarebbe un dxd Matrice di covarianza.

Perciò, per un set di dati che ha D caratteristiche, avremmo un mix di K distribuzioni gaussiane (dove K rappresenta il numero di cluster), ciascuno con un vettore medio e una matrice della varianza determinati.

Ma la nostra domanda è: “Come possiamo trovare la media e la varianza di ogni gaussiana??”

Per trovare questi valori, usiamo una tecnica chiamata Expectation-Maximization (IN).

Modelli di miscela gaussiana

L'assunto principale di questi modelli di mistura è che ci sia un certo numero di distribuzioni gaussiane, e ciascuna di queste distribuzioni rappresenta un gruppo. Perciò, un modello di miscela gaussiana tenta di raggruppare osservazioni che appartengono a una singola distribuzione.

I modelli di miscelazione gaussiana sono modelli probabilistici che utilizzano il raggruppamentoIl "raggruppamento" È un concetto che si riferisce all'organizzazione di elementi o individui in gruppi con caratteristiche o obiettivi comuni. Questo processo viene utilizzato in varie discipline, compresa la psicologia, Educazione e biologia, per facilitare l'analisi e la comprensione di comportamenti o fenomeni. In ambito educativo, ad esempio, Il raggruppamento può migliorare l'interazione e l'apprendimento tra gli studenti incoraggiando il lavoro.. Distribuzione fluida delle osservazioni in diversi gruppi, vale a dire, diverse distribuzioni gaussiane.

Ad esempio, il modello di miscela gaussiana di 2 distribuzioni gaussiane

Abbiamo due distribuzioni gaussiane: n (?₁, ?₁²) e n(?₂, ?₂²)

Qui, dobbiamo stimare un totale di 5 parametri:

= (P, ?₁, ?₁²,?₂, ?₂²)

dove p è la probabilità che i dati provengano dalla prima distribuzione gaussiana e 1-p che provengano dalla seconda distribuzione gaussiana.

Quindi, la funzione di densità di probabilità (PDF) del modello di miscela è dato da:

G (X |?) = p₁(X | ?₁, ?₁²) + (1-P) G₂(X | ?₂, ?₂² )

obbiettivo: Per adattare meglio una data densità di probabilità trovando = (P, ?₁, ?₁², ?₂, ?₂²) attraverso iterazioni EM.

Implementazione di GMM in Python

È ora di immergersi nel codice! Qui per l'implementazione, noi usiamo il Libreria Sklearn di Python.

Da sklearn, usiamo la classe GaussianMixture che implementa l'algoritmo EM per adattare una combinazione di modelli gaussiani. Dopo la creazione dell'oggetto, usando il GaussianMixture.fit possiamo apprendere un modello di miscela gaussiana dai dati di addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina.....

passo 1: Importa i pacchetti necessari

importa numpy come np
importa matplotlib.pyplot come plt
da sklearn.mixture import GaussianMixture

passo 2: creare un oggetto della classe Gaussian Mixture

gmm = miscela gaussiana(n_componenti = 2, pedaggio=0.000001)

passo 3: adatta l'oggetto creato al set di dati dato

gmm.fit(np.expand_dims(dati, 1))

passo 4: Stampa i parametri di 2 gaussiani in arrivo

Nr_gaussiano = 1
Stampa('Input Normal_distb {:}: μ = {:.2}, = {:.2}'.formato("1", Media1, Standard_dev1))
Stampa('Input Normal_distb {:}: μ = {:.2}, = {:.2}'.formato("2", media2, Standard_dev2))

Produzione:

Input Normal_distb 1: μ = 2.0, = 4.0

Input Normal_distb 2: μ = 9.0, = 2.0

passo 5: Parametri di stampa dopo la miscelazione 2 gaussiano

per mu, sd, p in zip(gmm.means_.appiattire(), np.sqrt(gmm.covariances_.flatten()), gmm.pesi_):
    Stampa('Normal_distb {:}: μ = {:.2}, = {:.2}, peso = {:.2}'.formato(Gaussian_nr, mu, sd, P))
    g_s = stats.norm(mu, sd).PDF(X) * P
    plt.trama(X, g_s, etichetta="sclero gaussiano");
    Nr_gaussiano += 1

Produzione:

Normal_distb 1: μ = 1,7, = 3,8, peso = 0,61

Normal_distb 2: μ = 8.8, = 2.2, peso = 0.39

passo 6: Traccia i grafici di distribuzione

sns.distplot(dati, contenitori=20, kde = falso, norm_hist=Vero)
gmm_sum = np.exp([gmm.score_samples(e.reshape(-1, 1)) per e in x]) 
plt.trama(X, gmm_sum, etichetta="miscela gaussiana");
plt.legend();

Produzione:

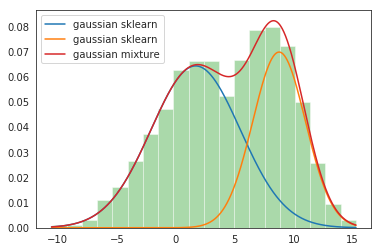
Questo completa la nostra implementazione GMM!!

Note finali

Grazie per aver letto!

Se ti è piaciuto e vuoi saperne di più, visita gli altri miei articoli sulla scienza dei dati e sull'apprendimento automatico facendo clic su Collegamento

Sentiti libero di contattarmi a Linkedin, E-mail.

Tutto ciò che non è stato menzionato o vuoi condividere i tuoi pensieri? Sentiti libero di commentare qui sotto e ti ricontatterò.

Circa l'autore

Chirag Goyal

Attualmente, Sto perseguendo il mio Bachelor of Technology (B.Tech) in informatica e ingegneria da Istituto indiano di tecnologia Jodhpur (IITJ). Sono molto entusiasta dell'apprendimento automatico, il apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute... e intelligenza artificiale.

I media mostrati in questo articolo su Algoritmo di massimizzazione delle aspettative non sono di proprietà di DataPeaker e sono utilizzati a discrezione dell'autore.

Imparentato