Supporta la regressione vettoriale nell'apprendimento automatico

Sbloccare un nuovo mondo con l'algoritmo di regressione vettoriale di supporto

Supporta macchine vettoriali (SVM) sono comunemente e ampiamente utilizzati per problemi di classificazione nell'apprendimento automatico. Ho fatto spesso affidamento su questo non solo nei progetti di machine learning, ma anche quando voglio un risultato veloce in un hackathon.

Ma SVM per l'analisi di regressione? Non avevo nemmeno considerato la possibilità per un po'!! E anche adesso, quando menziono “Supporta la regressione del vettore” contro i principianti dell'apprendimento automatico, Ho spesso un'espressione perplessa. Capisco: la maggior parte dei corsi e degli esperti non menziona nemmeno il supporto della regressione vettoriale (SVR) come algoritmo di apprendimento automatico.

Ma SVR ha i suoi usi, come vedrai in questo tutorial. Per prima cosa capiremo rapidamente cos'è SVM, prima di immergerci nel mondo della regressione del vettore di supporto e come implementarlo in Python.

Nota: Puoi conoscere le macchine vettoriali di supporto e i problemi di regressione nel formato del corso qui (È gratis!):

Questo è ciò che tratteremo in questo tutorial sulla regressione del vettore di supporto:

• Che cos'è una macchina vettoriale di supporto? (SVM)?
• Supporta gli iperparametri dell'algoritmo della macchina vettoriale
• Introduzione alla regressione del vettore di supporto (SVR)
• Implementazione della regressione del vettore di supporto in Python

Che cos'è una macchina vettoriale di supporto? (SVM)?

Quindi, Che cos'è esattamente Support Vector Machine? (SVM)? Inizieremo comprendendo SVM in termini semplici. Digamos que tenemos un diagrama de dos clases de etiquetas como se muestra en la siguiente figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline....:

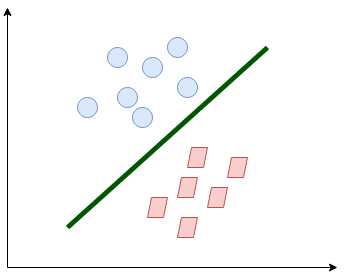
Puoi decidere quale sarà la linea di separazione?? Questo potrebbe esserti venuto in mente:

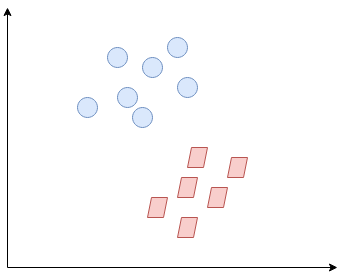
La linea separa un po' le classi. Questo è ciò che essenzialmente fa SVM: semplice separazione di classe. Ora, Quali sono i dati??

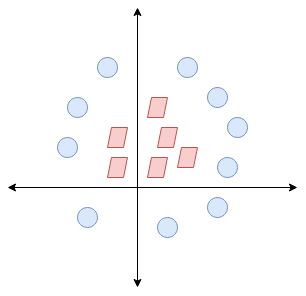
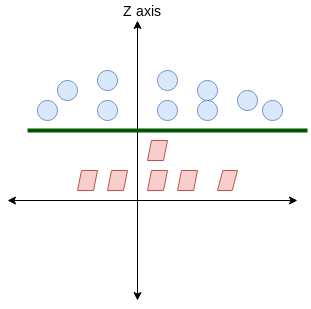
Qui, non abbiamo una linea semplice che separa queste due classi. Así que ampliaremos nuestra dimensione"Dimensione" È un termine che viene utilizzato in varie discipline, come la fisica, Matematica e filosofia. Si riferisce alla misura in cui un oggetto o un fenomeno può essere analizzato o descritto. In fisica, ad esempio, Si parla di dimensioni spaziali e temporali, mentre in matematica può riferirsi al numero di coordinate necessarie per rappresentare uno spazio. Comprenderlo è fondamentale per lo studio e... e introduciremos una nueva dimensión a lo largo del eje z. Ora possiamo separare queste due classi:

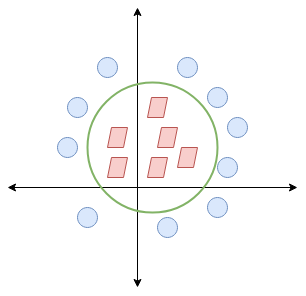
Quando trasformiamo questa linea nel piano originale, mappe al confine circolare come ho mostrato qui:

Questo è esattamente ciò che fa SVM!! Prova a trovare una linea / iperpiano (in uno spazio multidimensionale) che separa queste due classi. Quindi classificare il nuovo punto in base al fatto che si trovi sul lato positivo o negativo dell'iperpiano in base alle classi da prevedere.

Supporta gli iperparametri dell'algoritmo della macchina vettoriale (SVM)

Hay algunos parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... importantes de SVM que debe conocer antes de continuar:

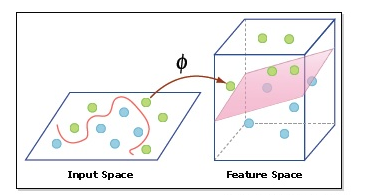
• Nucleo: Un kernel ci aiuta a trovare un iperpiano in uno spazio dimensionale superiore senza aumentare il costo computazionale. Generalmente, il costo computazionale aumenterà se la dimensione dei dati aumenta. Questo aumento di dimensione è necessario quando non riusciamo a trovare un iperpiano di separazione in una certa dimensione e dobbiamo spostarci in una dimensione superiore:

• Iperpiano: Questa è fondamentalmente una linea di demarcazione tra due classi di dati in SVM. Ma nella regressione del vettore di supporto, questa è la linea che verrà utilizzata per prevedere l'uscita continua
• Limite di decisione: Un confine decisionale può essere pensato come una linea di demarcazione (per semplificare) da una parte ci sono esempi positivi e dall'altra ci sono esempi negativi. In questa stessa linea, gli esempi possono essere classificati come positivi o negativi. Questo stesso concetto SVM si applicherà anche alla regressione del vettore di supporto

Per comprendere SVM da zero, Consiglio questo tutorial: Comprendere l'algoritmo Support Vector Machine (SVM) da esempi.

Introduzione alla regressione del vettore di supporto (SVR)

Supporta la regressione del vettore (SVR) utilizza lo stesso principio di SVM, ma per problemi di regressione. Prendiamoci qualche minuto per capire l'idea dietro SVR.

L'idea alla base della regressione del vettore di supporto

El problema de la regresión es encontrar una función que se aproxime al mapeo de un dominio de entrada a números reales sobre la base de una muestra de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina..... Quindi ora scaviamo più a fondo e capiamo come funziona davvero RVS..

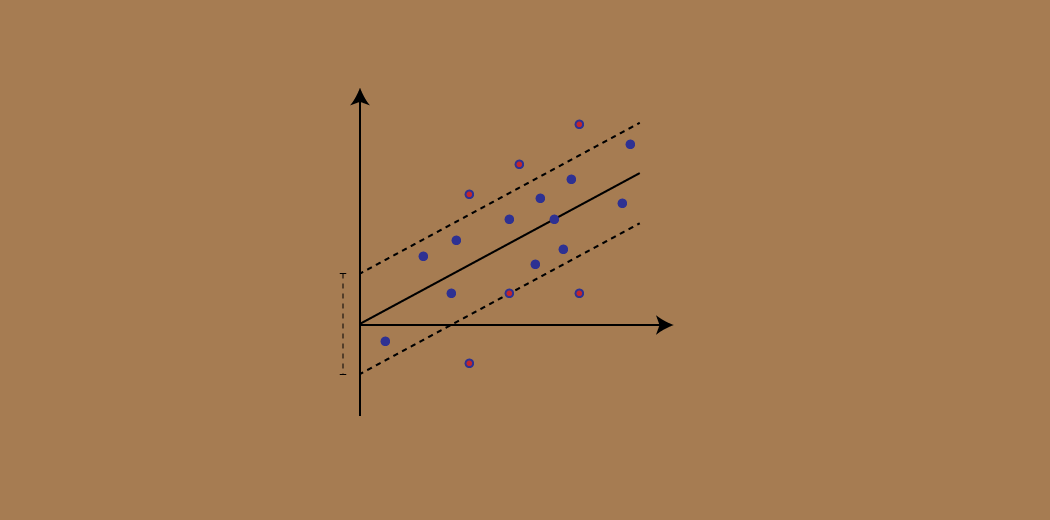
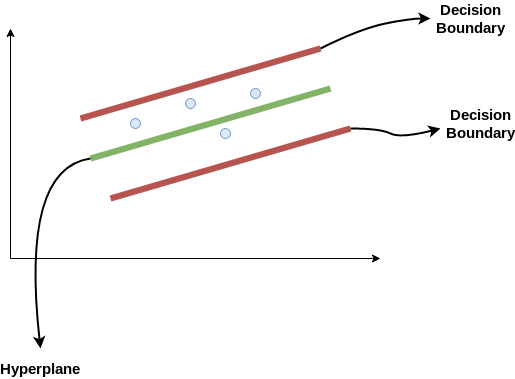
Considera queste due linee rosse come limite di decisione e la linea verde come iperpiano. Il nostro obiettivo, quando andiamo avanti con SVR, si tratta fondamentalmente di considerare i punti che si trovano all'interno della linea limite di decisione. La nostra migliore linea di adattamento è l'iperpiano che ha un numero massimo di punti.

La prima cosa che capiremo è qual è il limite di decisione (Il pericolo rosso si schiera!). Considera che queste linee sono a qualsiasi distanza, Diciamo “un”, dell'iperpiano. Quindi, queste sono le linee che tracciamo alla distanza ‘+ a’ già’ dell'iperpiano. Questo un’ nel testo è fondamentalmente noto come epsilon.

Supponendo che l'equazione dell'iperpiano sia la seguente:

Y = wx+b (equazione dell'iperpiano)

Quindi le equazioni limite di decisione diventano:

wx+b= +a

wx+b= -a

Perciò, qualsiasi iperpiano che soddisfi il nostro SVR dovrebbe soddisfare:

-un < E- wx+b < +un 

Il nostro obiettivo principale qui è decidere un limite decisionale a distanza'’ dell'iperpiano originale, in modo che i punti dati più vicini all'iperpiano o ai vettori di supporto si trovino all'interno di tale linea di confine.

Perciò, prenderemo solo quei punti che rientrano nel limite di decisione e hanno il tasso di errore più basso, o están dentro del MargineEl margen es un término utilizado en diversos contextos, como la contabilidad, la economía y la impresión. En contabilidad, se refiere a la diferencia entre los ingresos y los costos, lo que permite evaluar la rentabilidad de un negocio. En el ámbito editorial, el margen es el espacio en blanco alrededor del texto en una página, que facilita la lectura y proporciona una presentación estética. Su correcta gestión es esencial... de Tolerancia. Questo ci dà un modello più adatto.

Supporta l'implementazione della regressione vettoriale (SVR) e Python

È tempo di indossare i nostri cappelli da codifica!! In questa sezione, capiremo l'uso della regressione del vettore di supporto con l'aiuto di un set di dati. Qui, dobbiamo prevedere lo stipendio di un dipendente date alcune variabili indipendenti. Un classico progetto di analisi delle risorse umane!

passo 1: importare le librerie

passo 2: leggere il set di dati

passo 3: Ridimensionamento delle funzioni

Un set di dati del mondo reale contiene caratteristiche che variano in grandezza, unità e gamma. Sugeriría realizar la standardizzazioneLa standardizzazione è un processo fondamentale in diverse discipline, che mira a stabilire norme e criteri uniformi per migliorare la qualità e l'efficienza. In contesti come l'ingegneria, Istruzione e amministrazione, La standardizzazione facilita il confronto, Interoperabilità e comprensione reciproca. Nell'attuazione degli standard, si promuove la coesione e si ottimizzano le risorse, che contribuisce allo sviluppo sostenibile e al miglioramento continuo dei processi.... cuando la escala de una característica es irrelevante o engañosa.

Il ridimensionamento delle funzionalità aiuta fondamentalmente a normalizzare i dati all'interno di un intervallo particolare. Normalmente, diversi tipi di classi comuni contengono la funzione di ridimensionamento delle funzionalità per ridimensionare automaticamente le funzionalità. tuttavia, la classe SVR non è un tipo di classe comunemente usato, quindi dovremmo fare il ridimensionamento delle funzionalità con Python.

passo 4: adatta SVR al set di dati

Il kernel è la caratteristica più importante. Ci sono molti tipi di core: lineare, gaussiano, eccetera. Ciascuno viene utilizzato in base al set di dati. Per ulteriori informazioni su questo, leggi questo: Supporta la macchina vettoriale (SVM) in Python e R

passo 5. Prevedi un nuovo risultato

Quindi, la previsione per y_pred (6, 5) sarà 170,370.

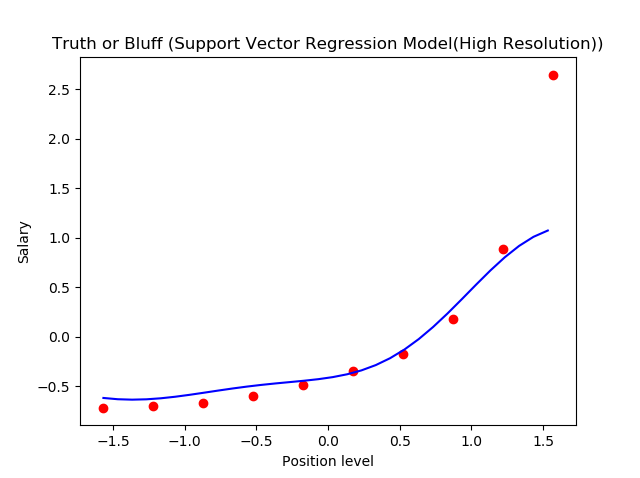
passo 6. Visualizzazione dei risultati SVR (para una risoluzioneIl "risoluzione" si riferisce alla capacità di prendere decisioni ferme e raggiungere gli obiettivi prefissati. In contesti personali e professionali, Implica la definizione di obiettivi chiari e lo sviluppo di un piano d'azione per raggiungerli. La risoluzione è fondamentale per la crescita personale e il successo in vari ambiti della vita, In quanto ti permette di superare gli ostacoli e mantenere la concentrazione su ciò che conta davvero.... más alta y una curva más suave)

Questo è ciò che otteniamo come output: la linea di miglior adattamento che ha un numero massimo di punti. Piuttosto accurato!

Note finali

Possiamo pensare alla regressione del vettore di supporto come la controparte di SVM ai problemi di regressione. SVR riconosce la presenza di non linearità nei dati e fornisce un modello di previsione competente.

Mi piacerebbe sentire i tuoi pensieri e idee sull'utilizzo di SVR per l'analisi di regressione.. Connettiti con me nella sezione commenti qui sotto e veniamo con!

Imparentato