Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
STRINGERE PER L'IMPATTO! MORSETTO! MORSETTO! MORSETTO!
UPS!!! Il nostro aereo si è schiantato, Ma per fortuna siamo tutti al sicuro. Siamo data scientist, Quindi vogliamo aprire la scatola nera e vedere quali cose casuali sono state registrate all'interno. sì, Passiamo al nostro argomento.
Cosa sono le foreste casuali?
Devi aver risolto almeno una volta un problema di probabilità nel tuo liceo in cui dovevi trovare la probabilità di ottenere una palla di un colore specifico da una borsa contenente palline di colori diversi, dato il numero di palline di ogni colore. Le foreste casuali sono semplici se proviamo a impararle tenendo presente questa analogia.
Le foreste casuali (RF) Sono fondamentalmente una borsa contenente n alberi decisionali (DT) che hanno un diverso set di iperparametri e sono addestrati su diversi sottoset di dati. Diciamo che ho 100 Alberi decisionali nella mia borsa della foresta casuale! Come ho appena detto, estos árboles de decisión tienen un conjunto diferente de hiperparámetros y un subconjunto diferente de datos de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina...., Quindi la decisione o la previsione data da questi alberi può variare notevolmente. Consideriamo che in qualche modo ho addestrato tutti questi 100 alberi con i rispettivi sottoinsiemi di dati. Ora chiederò ai cento alberi nella mia borsa qual è la loro previsione riguardo ai miei dati di test. Ora dobbiamo solo prendere una decisione su un esempio o su un dato di prova, Lo facciamo con un semplice voto. Seguiamo ciò che la maggior parte degli alberi ha previsto per quell'esempio.
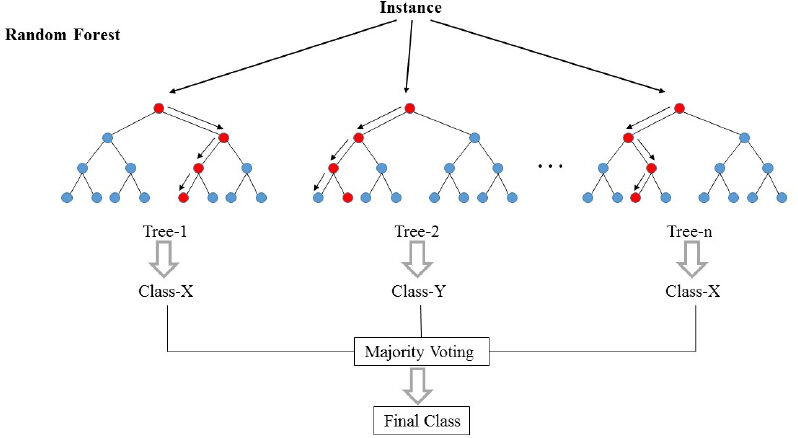
Nella foto sopra, Possiamo vedere come un esempio viene classificato utilizzando n alberi in cui la previsione finale viene effettuata prendendo un voto da tutti gli n alberi.
Nel linguaggio dell'apprendimento automatico, RF è anche chiamato metodo di assemblaggio o insaccamento. Penso che la parola bagging potrebbe derivare dall'analogia di cui abbiamo appena discusso!
Avviciniamoci un po' di più ai gerghi ML !!
El bosque aleatorio es básicamente un algoritmo de apprendimento supervisionatoL'apprendimento supervisionato è un approccio di apprendimento automatico in cui un modello viene addestrato utilizzando un set di dati etichettati. Ogni input nel set di dati è associato a un output noto, consentendo al modello di imparare a prevedere i risultati per nuovi input. Questo metodo è ampiamente utilizzato in applicazioni come la classificazione delle immagini, Riconoscimento vocale e previsione delle tendenze, sottolineandone l'importanza in.... Questo può essere utilizzato sia per le attività di regressione che per quelle di classificazione. Ma discuteremo del suo utilizzo per la classificazione perché è più intuitivo e più facile da capire. La foresta casuale è uno degli algoritmi più utilizzati grazie alla sua semplicità e stabilità.
Durante la creazione di sottoinsiemi di dati per gli alberi, la parola “a caso” entra in scena. Un sottoinsieme di dati viene creato selezionando casualmente un numero x di funzionalità (colonne) e numero di esempi (righe) Dal set di dati originale di n elementi e m esempi.
Le foreste casuali sono più stabili e affidabili di un semplice albero decisionale. Questo significa semplicemente dire che è meglio votare per tutti i ministri del gabinetto piuttosto che accettare semplicemente la decisione presa dal primo ministro.
Come abbiamo visto, le foreste casuali non sono altro che l'insieme degli alberi decisionali, Diventa fondamentale conoscere l'albero decisionale. Immergiamoci quindi negli alberi decisionali.
Che cos'è un albero decisionale?
In parole molto semplici, è un “Set di regole” Creato imparando un set di dati che può essere utilizzato per fare previsioni sui dati futuri. Cercheremo di capirlo con un esempio.
Di seguito è riportato un piccolo set di dati semplice. In questo set di dati, Le prime quattro funzionalità sono funzionalità indipendenti e le ultime sono le funzionalità dipendenti. Le caratteristiche indipendenti descrivono le condizioni meteorologiche in un dato giorno e la caratteristica dipendente ci dice se siamo stati in grado di giocare a tennis quel giorno o meno.
Ora proveremo a creare alcune regole utilizzando funzionalità indipendenti per prevedere le funzionalità dipendenti. Solo con l'osservazione, possiamo vedere che se Outlook è nuvoloso, Il gioco è sempre sì, Indipendentemente da altre caratteristiche. Allo stesso modo, Possiamo creare tutte le regole per descrivere completamente il set di dati. Ecco tutte le regole.
- R1: e (Prospettive = Soleggiato) E (Umidità = Alta) Quindi gioca = no
- R2: e (Prospettive = Soleggiato) E (Umidità = Normale) Quindi gioca = Sì
- R3: e (Prospettiva = Nuvoloso) Allora Riproduci = Sì
- R4: e (Prospettive = Pioggia) E (Vento = Forte) Quindi gioca = no
- R5 ·: e (Prospettiva = Pioggia) E (Vento = Debole) Quindi paga = Sì
Possiamo facilmente trasformare queste regole in un diagramma ad albero. Ecco il grafico ad albero.
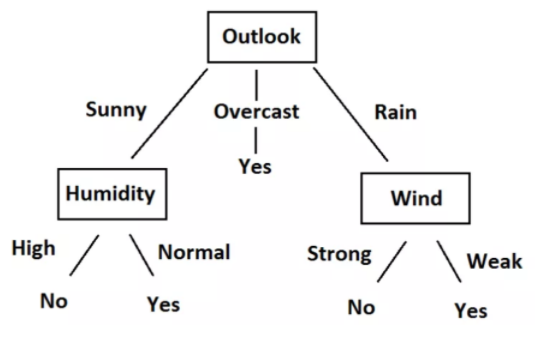
Quando si esaminano i dati, Le regole e l'albero, Capirete che ora possiamo prevedere se dobbiamo giocare a tennis o meno, data la situazione climatica basata su caratteristiche indipendenti. L'intero processo di creazione di regole per un dato dato non è altro che l'addestramento del modello dell'albero decisionale.
Potremmo impostare regole e creare un albero semplicemente guardando qui perché il set di dati è così piccolo. Ma, Come si addestra l'albero decisionale su un set di dati più ampio?? Per quello, Abbiamo bisogno di conoscere un po' di matematica. Ora cercheremo di capire la matematica dietro l'albero decisionale.
Concetti matematici alla base dell'albero decisionale
Questa sezione è composta da due concetti importanti: Entropia e guadagno di informazioni.
entropia
La entropía es una misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... de la aleatoriedad de un sistema. L'entropia dello spazio campionario S è il numero atteso di bit necessari per codificare la classe di un membro estratto casualmente di S. Qui abbiamo 14 righe nei nostri dati, affinché 14 membri.
Entropia E (S) = -∑p (X) * tronco d'albero2(P (X))
L'entropia del sistema viene calcolata utilizzando la formula precedente, Dove p (X) è la probabilità di ottenere la classe x di quelli 14 membri. Abbiamo due classi qui, uno è Sì e l'altro è No nella colonna Riproduci. Ho 9 Sì e 5 Non nel nostro set di dati. Quindi, Il calcolo dell'entropia qui sarà il seguente
E (S) = -[P(Sì)*tronco d'albero(P(Sì))+ P(No)*tronco d'albero(P(No))]= -[(9/14)*tronco d'albero((9/14))+ (5/14*tronco d'albero((5/14)))]= 0,94
Guadagno di informazioni
Il guadagno di informazione è la quantità di cui l'entropia del sistema viene ridotta a causa della divisione che abbiamo fatto. Abbiamo creato l'albero utilizzando le osservazioni. Ma, Come abbiamo deciso che avremmo dovuto prima suddividere i dati in base a Outlook e non ad altre funzioni?? Il motivo è che questa divisione stava riducendo l'entropia della quantità massima, Ma l'abbiamo fatto intuitivamente nell'esempio sopra.
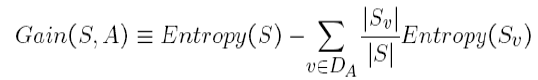
La divisione dell'albero sopra ci mostra che 9 SI e 5 Non sono stati divisi come (2 E, 3 n), (4 E, 0 n), (3 E, 2 n), quando facciamo la divisione secondo la prospettiva. I valori di E al di sotto di ogni divisione mostrano i valori di entropia considerandosi come un sistema completo e utilizzando la formula di entropia di cui sopra. Dopo, Abbiamo calcolato il guadagno di informazioni per la suddivisione prospettica utilizzando la formula del guadagno sopra.
Allo stesso modo, Possiamo calcolare il guadagno di informazioni per ogni divisione di funzionalità in modo indipendente. E otteniamo i seguenti risultati:
- Guadagnare (S, Prospettiva) = 0,247
- Guadagnare (S, umidità) = 0,151
- Guadagnare (S, vento) = 0.048
- Guadagnare (S, temperatura) = 0.029
Possiamo vedere che stiamo ottenendo il massimo guadagno di informazioni dividendo la funzione Outlook. Ripetiamo questa procedura per creare l'intero albero. Spero ti sia piaciuto leggere l'articolo. Se ti piace l'articolo, Condividilo con i tuoi colleghi e amici. Buona lettura!!!
