catena di Markov | Caratteristiche e applicazioni della catena di Markov

Questo articolo è stato pubblicato come voce per il Blogathon sulla scienza dei dati.

introduzione

Le catene di Markov sono eccezionalmente utili per modellare un processo stocastico a spazio discreto a tempo discreto di vari domini come la finanza. (movimento del prezzo delle azioni), Algoritmi di PNL (trasduttori a stato finito, Modello Markov nascosto per l'etichettatura POS), o anche in ingegneria fisica ( movimento browniano).

Tenendo conto dell'immensa utilità di questo concetto in vari domini e della sua fondamentale importanza per un numero significativo di algoritmi nella scienza dei dati, tratteremo in questo articolo i seguenti aspetti della catena di Markov:

1. Formulazione della catena di Markov e spiegazione intuitiva
2. Aspetti e caratteristiche di una catena di Markov
3. Applicazioni e casi d'uso

Formulazione della catena di Markov e spiegazione intuitiva

Per capire cos'è una catena di Markov, prima vediamo cos'è un processo stocastico, poiché la catena di Markov è un tipo speciale di processo stocastico.

Un processo stocastico è definito come un insieme di variabili casuali X = {X_T: t∈T} definito in uno spazio di probabilità comune, prendendo valori in un insieme comune S (spazio degli stati), e indicizzato da un insieme T, Non spesso [0, ?) e pensato come tempo (rispettivamente discreta o continua) (Oliver, 2009). Significa che abbiamo osservazioni in un certo momento e il risultato è casuale variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi..... In poche parole, un processo stocastico è qualsiasi processo che descrive l'evoluzione nel tempo di un fenomeno casuale.

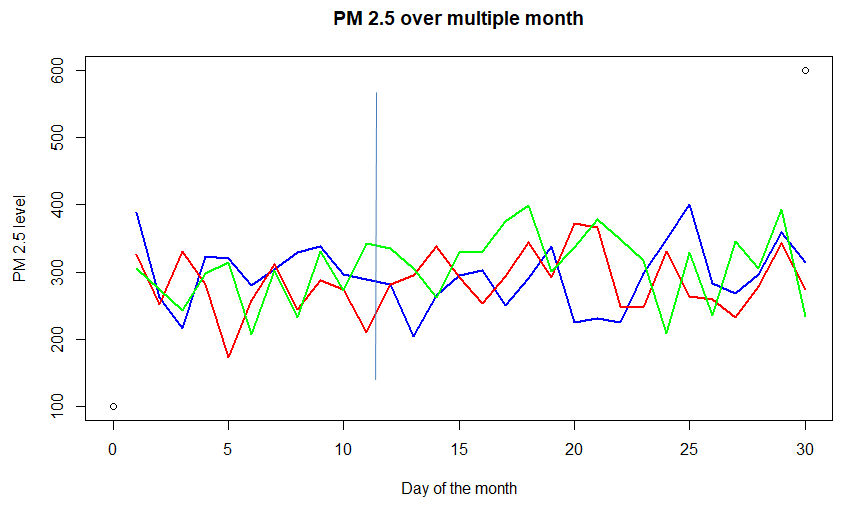
Considera il grafico sopra della concentrazione di PM (particolato) 2.5 nell'aria sopra una città per diversi mesi. Ognuna delle linee colorate -rosso, blu, e verde – (chiamato percorso-campione) rappresenta una funzione casuale del tempo. Anche, considera ogni giorno (diciamo il 15 di ogni mese), rappresenta una variabile casuale. Quindi può essere considerato come un processo stocastico, cioè un processo che accetta input funzionali diversi in momenti diversi. Questo particolare esempio è un caso per tempo discreto (poiché il tempo non è continuo, osservato una volta al giorno) insieme a uno stato continuo (può assumere qualsiasi valore positivo, non necessariamente un intero).

Ora che abbiamo un'intuizione di base di un processo stocastico, scendiamo a capire uno dei concetti matematici più utili per la Data Science: Catene di Markov!

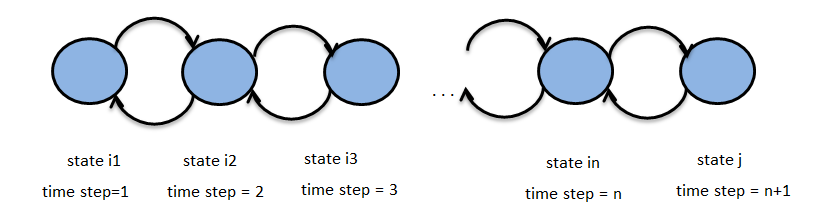
La figura sopra rappresenta una catena di Markov, con stati i₁, io₂ ,… , io_n , j per i passi temporali 1, 2, .., n+1. Permettere {INSIEME A_n}_n∈N essere il processo stocastico sopra con spazio degli stati S. N ecco l'insieme degli interi e rappresenta il Impostazione dell'ora e Z_n rappresenta lo stato della catena di Markov al tempo n. Supponiamo di avere la proprietà :

P(INSIEME A_n+1 = j | INSIEME A_n = io_n , INSIEME A_n-1 = io_n-1 , … , INSIEME A₁ = io₁) = P(INSIEME A_n+1 = j | INSIEME A_n = io_n)

poi {INSIEME A_n}_n∈N si chiama catena di Markov.

Questo termine P(INSIEME A_n+1 = j | INSIEME A_n= io_n) è chiamato probabilità di transizione. Quindi possiamo vedere intuitivamente che per descrivere probabilisticamente la catena di Markov, abbiamo bisogno (un) la distribuzione dello stato iniziale e (B) probabilità di transizione.

Prendiamo la catena di Markov mostrata di seguito per comprendere questi due termini in modo più formale,

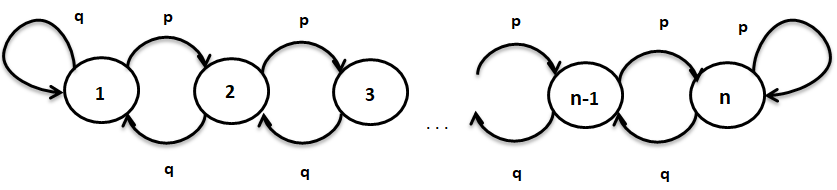
Nella catena di Markov sopra, gli stati sono 1, 2, …, n e la probabilità di passare da qualsiasi stato k a k+1 (per k=1, 2, …, n-1) è p e passare dallo stato k a k-1 è q, dove"DOVE" è un termine in inglese che si traduce come "dove" in spagnolo. Utilizzato per porre domande sulla posizione delle persone, Oggetti o eventi. In contesti grammaticali, Può funzionare come avverbio di luogo ed è fondamentale nella formazione delle domande. La sua corretta applicazione è essenziale nella comunicazione quotidiana e nell'insegnamento delle lingue, facilitare la comprensione e lo scambio di informazioni su posizioni e direzioni.... q = 1-p.

• Il distribuzione dello stato iniziale è definito come

Pi₍₀₎ = [P(X₀=1), P(X₀=2), … , P(X₀ = n)]

L'espressione precedente è un vettore riga con elemento che denota la probabilità che la catena di Markov abbia lo stato i, dove io = 1, 2,…, n. Tutti gli elementi di questo vettore si sommano a 1.

• il matrice di probabilità di transizione è come mostrato di seguito :

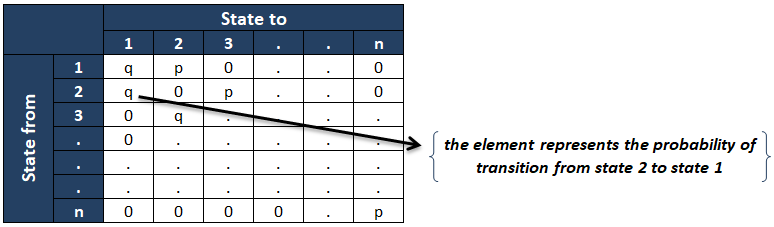
El ij^ns elemento della matrice di probabilità di transizione rappresenta il la probabilità condizionata della catena è nello stato j poiché era nello stato i al momento precedente. Se la matrice di probabilità di transizione non dipende da “n” (tempo metereologico), allora la catena si chiama il Catena di Markov omogenea.

Aspetti e caratteristiche di una catena di Markov

In questa sezione, vedremo i seguenti aspetti principali di una catena di Markov:

• Ora del primo colpo: G_io(K)
• Tempo di impatto medio (tempo di assorbimento): h_UN(K)

Lo scopo delle due analisi precedenti è che se abbiamo un insieme di stati desiderati (diciamo A), e vogliamo calcolare quanto tempo ci vorrà per raggiungere lo stato desiderato.

Prima ora di colpo

Immaginare, se vogliamo conoscere la probabilità (condizionale) che la nostra catena Markov, che inizia in qualche stato iniziale k, raggiungere lo stato l (uno dei tanti stati desiderati in A) fintanto che raggiunge qualsiasi stato in A. Come lo facciamo? Quello?

Capiamo definendo alcuni termini di base. Lascia che T_UN essere il primo tempo necessario per raggiungere uno degli stati nell'insieme A e k essere uno stato nello spazio degli stati ma non in A.

Lascia che g_io(K) essere definita come la probabilità condizionata di raggiungere lo stato l al tempo T_UN dallo stato k.

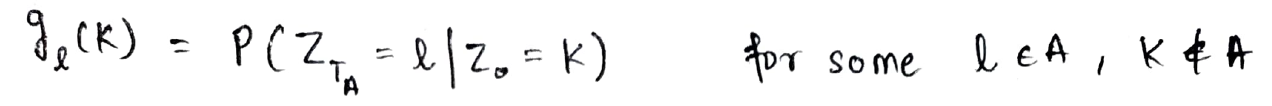
Ora, usando la proprietà di Markov, Consideriamo il passaggio dello stato nel tempo = 0 allo stato nel tempo = T_UN come passare lo stato nel tempo = 0 allo stato nel tempo = 1 e poi vai da uno stato all'altro = 1 allo stato nel tempo = TA. Lo stesso è rappresentato di seguito:

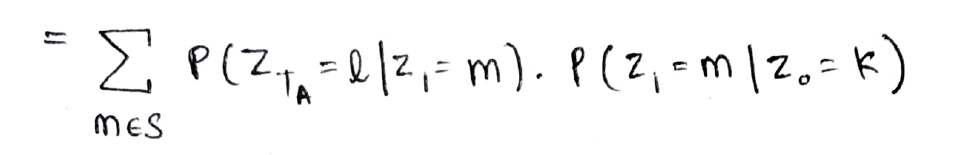
L'equazione di cui sopra può essere interpretata graficamente come mostrato di seguito, vale a dire, nel primo passaggio puoi passare dallo stato k a uno qualsiasi degli stati m in un passaggio e poi andare in T_UN-1 passaggio dallo stato m allo stato desiderato l.

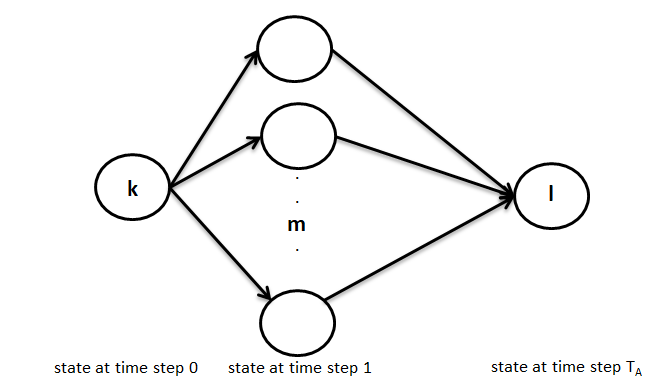
Ora, il primo termine può essere rappresentato come g_io(m) e il secondo termine rappresenta la probabilità di transizione dallo stato k allo stato m

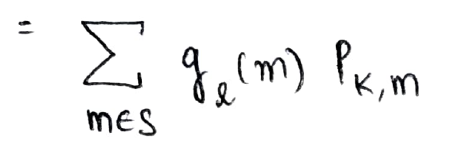
Questo è il modo ricorsivo in cui calcoliamo la probabilità desiderata e viene chiamato l'approccio usato sopra Analisi del primo passo (mentre lo analizziamo in termini del primo passo che lo stato compie in tempo = 0 allo stato nel tempo = 1)

Tempo medio di successo

Utilizzando un approccio simile come sopra, possiamo anche calcolare il tempo medio (previsto) per raggiungere un insieme desiderato di stati (diciamo A) da uno stato k su A.

Definiamo h_UN(K) come il tempo atteso necessario per raggiungere un insieme A dallo stato k. Questo è definito come mostrato di seguito:

Ora che sappiamo qual è l'analisi del primo passaggio, Perché non usarlo di nuovo??

Quindi, ora scriviamo il termine di attesa in termini del primo passo (vale a dire, raggiungere lo stato Z₁) Come mostrato di seguito:

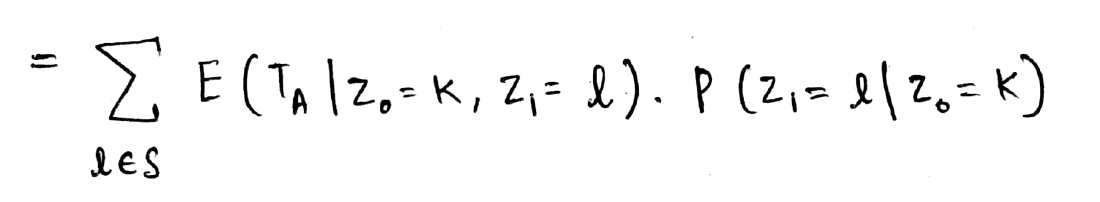
Ora, usando la proprietà di Markov, possiamo eliminare la Z₀ termine come conosciamo lo stato in Z₁. Il secondo termine nel prodotto precedente è la probabilità di transizione dallo stato k allo stato l (abbiamo visto questo concetto così tanto che ora sembra un calcolo 2 + 2 = 4 ?)

Si noti che il termine di aspettativa di seguito è in termini di Z₁ (e non Z₀) e quindi non possiamo scriverlo direttamente come h_UN(K). Perciò, usiamo un trucco matematico, noi aggiungiamo 1 in attesa e sottraiamo 1 anche in modo che possiamo scrivere matematicamente lo stato come Z₀ = l

E ora possiamo scriverlo come h_UN(K).

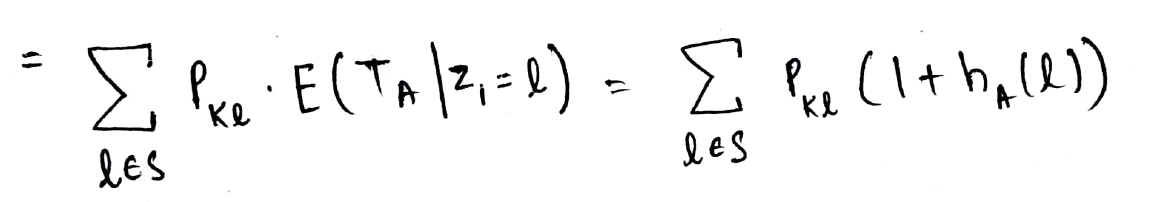
Questo è il modo ricorsivo per calcolare l'aspettativa desiderata!!

Ora conosciamo l'approccio fondamentale per derivare qualsiasi proprietà di Markov con i due nuovi strumenti che abbiamo: Comprensione di matrice di probabilità di transizione e Approccio di analisi del primo passo.

Applicazioni e casi d'uso

Dal momento che ora siamo a nostro agio con il concetto e gli aspetti di una catena di Markov, Esploriamo e comprendiamo intuitivamente la seguente applicazione e casi d'uso delle catene di Markov.

• PNL: modello Markov nascosto per l'etichettatura del punto vendita
• Cammina a caso come una catena di Markov

PNL: modello Markov nascosto per l'etichettatura del punto vendita

Etichettatura di una parte del discorso (POS) è un'importante applicazione della PNL. L'obiettivo in questi problemi è etichettare ogni parola in una data frase con un POS appropriato (sostantivo, verbo, avverbio, eccetera.). Nel modello, abbiamo probabilità di transizione dell'etichetta, vale a dire, poiché l'etichetta della parola precedente è detta t_i-1, il t_io sarà l'etichetta della parola corrente. E il secondo concetto del modello è la probabilità che data l'etichetta della parola corrente sia t_io, la parola sarà w_io. Per dirla più chiaramente: il modello di Markov nascosto è un tipo di Modelli generativi (imposta) in cui gli stati nascosti (qui etichette POS) sono considerati dati e i dati osservati sono considerati generati.

il t_io Nel figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline.... Quanto segue si riferisce ai tag POS dello stato YW_io si riferisce alle parole emesse dagli stati.

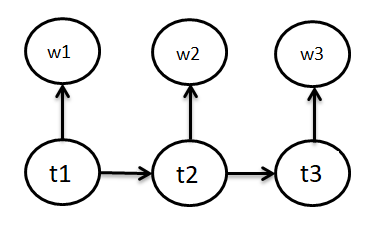
Ora, diamo un'occhiata più da vicino all'elemento del modello per vedere il processo di Markov in esso ancora più chiaramente. Gli elementi del modello di Markov nascosto sono:

• Un insieme di stati: qui Etichette POS
• L'uscita di ogni stato: qui 'parola'’
• stato iniziale: qui inizio la frase
• Probabilità di transizione di stato: qui P (T_Nord | T_n-1)

Oltre ad essere molto utile in questo aspetto della PNL, trasduttori a stato finito e molti altri algoritmi sono basati su catene di Markov.

passeggiata casuale

Un altro fenomeno interessante è quello del Random walk, che di nuovo è una catena di Markov.

Consideriamo la passeggiata casuale, come mostrato sopra, vale a dire, il movimento di un passo avanti da qualsiasi stato può avvenire con probabilità p e il movimento indietro di un passo può avvenire con probabilità q. Qui il movimento in avanti dallo stato k a k + 1 dipende solo dallo stato k e, così, Random Walk è una catena di Markov.

Ora, facciamo un passo avanti e comprendiamo la passeggiata casuale come una catena di Markov usando la simulazione. Qui consideriamo il caso del cammino unidimensionale, dove la persona può fare un passo avanti o indietro di qualsiasi dimensione (dimensione> = 1) con uguale probabilità.

Qui, ho rintracciato 30 passeggiate casuali per sviluppare l'intuizione intorno al fenomeno. Qui, lo stato iniziale della catena di Markov è 0 (zero passi cumulativi inizialmente). Le cose da tenere a mente sono:

• Lo spazio degli stati e il tempo impostato sono entrambi discreti (interi)
• È visivamente chiaro che in ogni dato momento, lo stato successivo è determinato solo dallo stato corrente e le fasi temporali dietro l'intervallo temporale corrente non aiutano a prevedere dove sarà lo stato della catena nella fase temporale successiva.
• Poiché la probabilità di movimento in avanti è la stessa di quella di movimento all'indietro, il valore atteso del numero cumulativo di passi è 0.

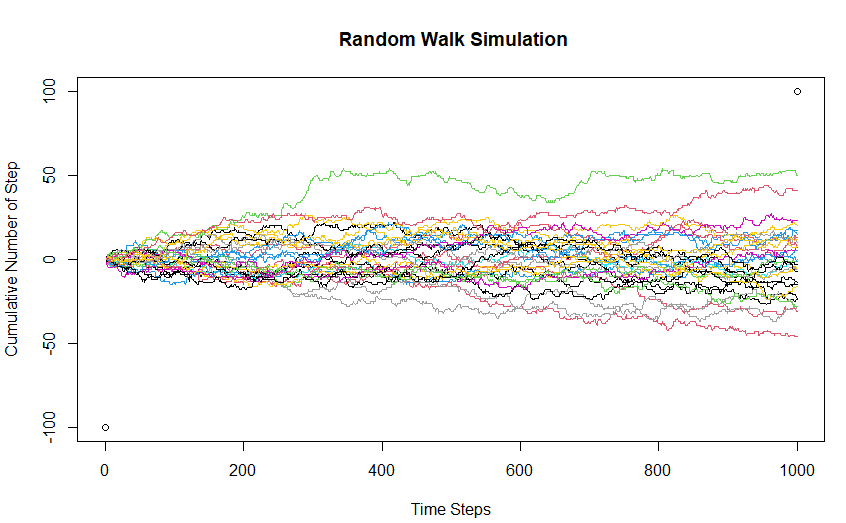
Di seguito è riportato il codice per simulare una passeggiata casuale di base in R:

complotto(C(0,1000),C(-100,100), xlab = "Passi temporali", ylab = "Numero cumulativo di passaggi" , principale = " Simulazione di camminata casuale")
per (io in 1:30) {
  X <- as.intero(normale(1000))
  Linee(cumsum(X), tipo = "io", col=campione(1:10,1)) 
}

La catena di Markov è una tecnica molto potente ed efficace per modellare un processo stocastico di tempo e spazio discreti.. La comprensione delle due precedenti applicazioni insieme al concetto matematico spiegato può essere utilizzata per comprendere qualsiasi tipo di processo di Markov.

Nota sull'autore: Sono uno studente PGDBA (Diploma di laurea in analisi aziendale) e IIM Calcutta, IIT Kharagpur e ISI Kolkata, e ho completato il mio B.TECH da IIT DELHI e ho un'esperienza lavorativa di ~ 3,5 anni nell'analisi avanzata.

Sentiti libero di contattare per qualsiasi discussione sull'argomento a parte tyagi | LinkedIn oppure scrivimi una mail a [e-mail protetta]

Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato