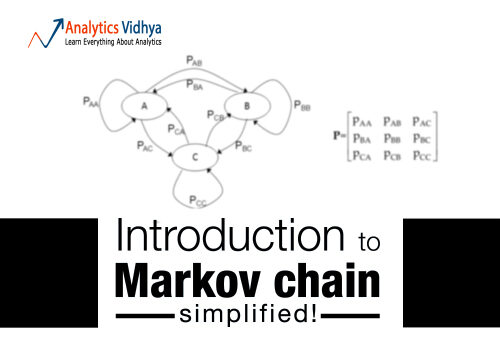
La catena di Markov è un concetto semplice che può spiegare i processi in tempo reale più complicati. Riconoscimento vocale, identificatori di testo, il riconoscimento del percorso e molti altri strumenti di intelligenza artificiale utilizzano in qualche modo questo semplice principio chiamato catena di Markov. In questo articolo illustreremo quanto sia facile comprendere e implementare questo concetto in R.
La catena di Markov si basa su un principio di “perdita di memoria”. In altre parole, lo stato successivo del processo dipende solo dallo stato precedente e non dalla sequenza degli stati. Questa semplice ipotesi facilita il calcolo della probabilità condizionata e consente di applicare questo algoritmo in vari scenari.. In questo articolo ci limiteremo a una semplice catena di Markov. Nei guai nella vita reale, generalmente usiamo il modello di Markov latente, che è una versione altamente evoluta della catena di Markov. Parleremo anche di una semplice applicazione della catena di Markov nel prossimo articolo..
Un semplice caso aziendale
Coca-Cola e Pepsi sono le uniche aziende nel paese X. Un'azienda di bevande analcoliche vuole collegarsi con uno di questi concorrenti. Assumono una società di ricerche di mercato per scoprire quale dei marchi avrà una quota di mercato più elevata dopo 1 mio. Attualmente, Pepsi possiede il 55% e Coca-Cola possiede il 45% di quota di mercato. Di seguito le conclusioni tratte dalla società di ricerche di mercato:
P (P-> P): Probabilità che un cliente manterrà il marchio Pepsi per un mese = 0,7
P (P-> C): probabilità che un cliente passi da Pepsi a Coca-Cola in un mese = 0,3
P (C-> C): Probabilità che un cliente rimanga con il marchio Coca Cola per un mese = 0.9
P (C-> P): Probabilità che un cliente passi da Coca-Cola a Pepsi in un mese = 0,1
Possiamo vedere chiaramente che i clienti tendono a rimanere fedeli alla Coca-Cola, ma Coca-Cola ha attualmente una quota di portafoglio inferiore. Perciò, non possiamo essere sicuri della raccomandazione senza fare alcuni calcoli di transizione.
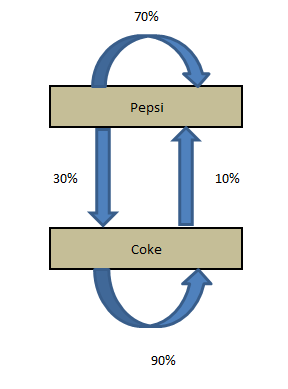
Diagramma di transizione
Le quattro affermazioni fatte dalla società di ricerca possono essere strutturate in un semplice diagramma di transizione.
Il diagramma mostra semplicemente le transizioni e l'attuale quota di mercato. Ora, se vogliamo calcolare la quota di mercato dopo un mese, dobbiamo fare i seguenti calcoli:
Quota di mercato (T + 1) Pepsi = quota di mercato attuale di Pepsi * P (P-> P) + L'attuale quota di mercato di Coca-Cola * P (C-> P)
Quota di mercato (T + 1) Coca-Cola = quota di mercato attuale di Coca-Cola * P (C-> C) + L'attuale quota di mercato di Pepsi * P (P-> C)
Questi calcoli possono essere eseguiti semplicemente osservando la seguente moltiplicazione matriciale:
Matrice di transizione dello stato attuale X = stato finale
Come possiamo vedere, vediamo chiaramente che Pepsi, anche se ora ha una quota di mercato più elevata, avrà una quota di mercato inferiore dopo un mese. Questo semplice calcolo è chiamato catena di Markov.. Se la matrice di transizione non cambia nel tempo, possiamo prevedere la quota di mercato in qualsiasi momento futuro. Facciamo lo stesso calcolo per 2 mesi dopo.
Calcoli dello stato stazionario
Oltre al business case che ci riguarda, l'azienda di bibite vuole ridurre il divario nella quota di mercato dell'azienda Coke e Pepsi a lungo termine. Questo li aiuterà a definire la giusta strategia di costo mentre si tuffano in Coca-Cola.. La quota di Pepsi continuerà a diminuire fino a un punto in cui il numero di clienti che lasciano Pepsi e il numero di clienti che si adattano a Pepsi è lo stesso. Perciò, dobbiamo soddisfare le seguenti condizioni per trovare le proporzioni dello stato stazionario:
Pepsi MS * 30% = Coca-Cola MS * 10% …………………………………………… ..1
Pepsi MS + Coca-Cola MS = 100% …………………………………………………… 2
4 * Pepsi MS = 100% => Pepsi MS = 25% e Coca-Cola MS = 75%
Formuliamo un algoritmo per trovare lo stato stazionario. Dopo lo stato stazionario, moltiplicando lo stato iniziale con la matrice di transizione darà lo stato iniziale stesso. Perciò, la matrice che può soddisfare la seguente condizione sarà le proporzioni finali:
Stato iniziale X Matrice di transizione = Stato iniziale
Risolvendo l'equazione di cui sopra, possiamo trovare la matrice di stato stazionario. La soluzione sarà la stessa di [25%,75%].
Ora risolviamo l'esempio precedente in R.
Implementazione in R
passo 1: creando una matrice di transizione e una catena di Markov a tempo discreto
Produzione
trans_mat [,1] [,2] [1,] 0.7 0.3 [2,] 0.1 0.9 #create the Discrete Time Markov Chain MC 1 UN 2 - Catena di Markov discreta dimensionale definita dai seguenti stati: Pepsi, Coke The transition matrix (per righe) è definito come segue: Pepsi Coke Pepsi 0.7 0.3 Coke 0.1 0.9
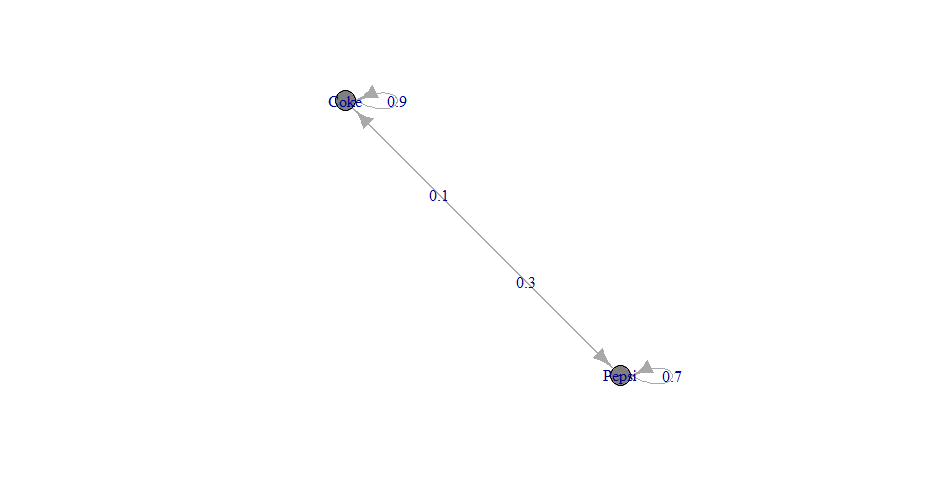
Trama
passo 2: Calcola la quota di mercato dopo 1 mese e 2 mesi
Produzione
#Market Share after one month Pepsi Coke 0.43 0.57 #Market Share after two month Pepsi Coke 0.358 0.642
passo 3: Creazione di una matrice a stato stazionario
Produzione
Pepsi Coca-Cola 0.25 0.75
Note finali
In questo articolo ti presentiamo le equazioni della catena di Markov, terminologia e sua implementazione in R. Discutiamo anche di come semplici equazioni possono essere scalate usando la moltiplicazione di matrici.. Useremo queste terminologie e framework per risolvere un esempio di vita reale nel prossimo articolo.. También le presentaremos conceptos como nodoNodo è una piattaforma digitale che facilita la connessione tra professionisti e aziende alla ricerca di talenti. Attraverso un sistema intuitivo, Consente agli utenti di creare profili, condividere esperienze e accedere a opportunità di lavoro. La sua attenzione alla collaborazione e al networking rende Nodo uno strumento prezioso per chi vuole ampliare la propria rete professionale e trovare progetti in linea con le proprie competenze e obiettivi.... absorbente y cadena de Markov regular para resolver el ejemplo.
L'articolo ti è stato utile?? Questo articolo ha risolto i tuoi problemi esistenti?? Hai mai usato una semplice catena Markov prima?? Se lo ha fatto, condividi con noi i tuoi pensieri sull'argomento.