introduzione
Gli algoritmi di apprendimento automatico sono classificati in tre tipi: apprendimento supervisionatoL'apprendimento supervisionato è un approccio di apprendimento automatico in cui un modello viene addestrato utilizzando un set di dati etichettati. Ogni input nel set di dati è associato a un output noto, consentendo al modello di imparare a prevedere i risultati per nuovi input. Questo metodo è ampiamente utilizzato in applicazioni come la classificazione delle immagini, Riconoscimento vocale e previsione delle tendenze, sottolineandone l'importanza in..., Apprendimento non supervisionatoL'apprendimento non supervisionato è una tecnica di apprendimento automatico che consente ai modelli di identificare modelli e strutture nei dati senza etichette predefinite. Attraverso algoritmi come k-means e analisi delle componenti principali, Questo approccio viene utilizzato in una varietà di applicazioni, come la segmentazione dei clienti, Rilevamento delle anomalie e compressione dei dati. La sua capacità di rivelare informazioni nascoste lo rende uno strumento prezioso... y aprendizaje reforzado. Il clustering di mezzi K è una tecnica di apprendimento automatico non supervisionata. Cuando no se proporciona la variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... de salida o respuesta, questo algoritmo viene utilizzato per classificare i dati in diversi gruppi per comprenderli meglio. Conosciuto anche come approccio di apprendimento automatico basato sui dati, poiché raggruppa i dati in base a modelli nascosti, conoscenze e somiglianze nei dati.
Considera il seguente diagramma: se ti viene chiesto di raggruppare le persone nella foto in diversi gruppi o gruppi e non sai nulla di loro, cercherò sicuramente di individuare le qualità, caratteristiche o attributi fisici che queste persone condividono. Dopo aver osservato queste persone, si conclude che possono essere segregati in base alla loro altezza e larghezza; dal momento che non hai alcuna conoscenza preliminare di queste persone. K significa che il clustering esegue un lavoro approssimativamente equivalente. Prova a classificare i dati in gruppi in base a somiglianze e schemi nascosti. “K” in clustering di K-mean si riferisce al numero di cluster che l'algoritmo genererà nei dati.
K-Mezzi raggruppamento: Come funziona?
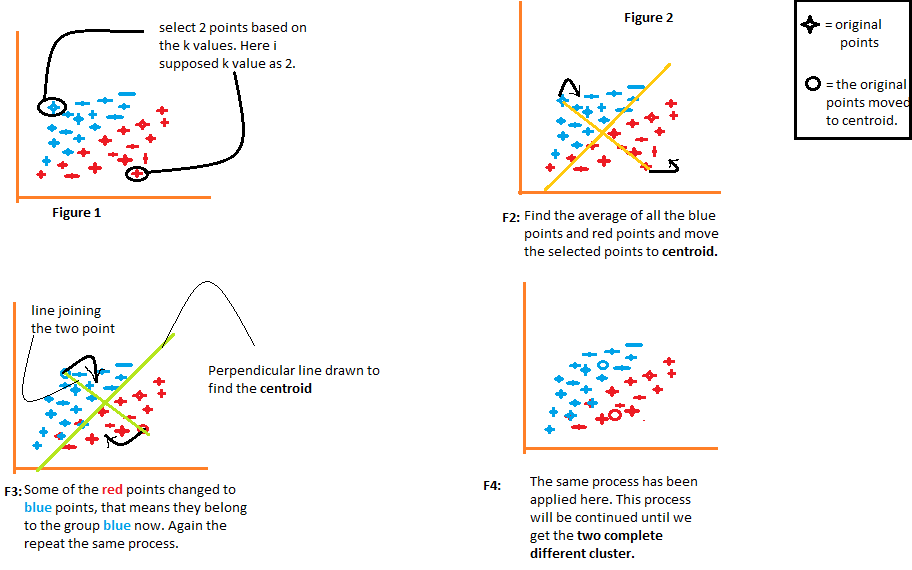
1) L'algoritmo sceglie arbitrariamente il numero k di centroidi, como se indica en la figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline.... 1 dal diagramma seguente. Dove k è il numero di cluster che l'algoritmo creerebbe. Diciamo che vogliamo che l'algoritmo crei due gruppi dai dati, quindi imposteremo il valore di k a 2.
2) Quindi raggruppare i dati in due parti utilizzando le distanze calcolate da entrambi i centroidi., come illustrato in Figura 2. La distanza di ogni punto da entrambi i centroidi viene calcolata singolarmente e successivamente verrà aggiunta al gruppo di quel centroide con cui viene calcolata la distanza. più corto.
L'algoritmo disegna anche una linea che unisce i centroidi e una linea perpendicolare che cerca di raggruppare i dati in due gruppi.
3) Una volta che tutti i punti dati sono stati raggruppati in base alle loro distanze minime dai corrispondenti centroidi, l'algoritmo calcola la media di ciascun gruppo. Quindi vengono confrontati i valori medi e del baricentro di ciascun gruppo. Se il valore del baricentro è diverso dalla media, quindi il baricentro viene spostato al valore medio del gruppo. Sia il baricentro “rosso” Come la “blu” sono ricollocati sulla media del gruppo in figura 3 dal diagramma seguente.
Raggruppa i dati ancora una volta usando questi centroidi aggiornati. A causa del cambiamento nelle posizioni dei baricentri, alcuni punti dati possono ora essere spostati nell'altro gruppo.
4) Ancora, calcola la media e la confronta con il baricentro dei gruppi appena generati. Se entrambi sono diversi, il baricentro verrà riposizionato nella media del gruppo. Questo processo di calcolo della media e confronto con il baricentro viene ripetuto finché i valori del baricentro e della media sono uguali. (valore del centroide = media di gruppo). Questo è il punto in cui l'algoritmo ha segmentato i dati in "gruppi K"’ (2 in questo caso).
Come scoprire qual è il valore ottimale di k?
Il primo passo è fornire un valore per k. Ogni passo successivo eseguito dall'algoritmo è completamente dipendente dal valore specificato di k. Questo valore di k aiuta l'algoritmo a determinare il numero di cluster da generare. Ciò sottolinea l'importanza di fornire il valore preciso di k. Qui, un metodo noto come “metodo del gomito” per determinare il valore corretto di k. Questo è un grafico di 'Numero di cluster K’ contro “Totale all'interno della somma dei quadrati”. I valori discreti di k sono tracciati sull'asse x, mentre le somme dei quadrati dei gruppi sono tracciate sull'asse y.
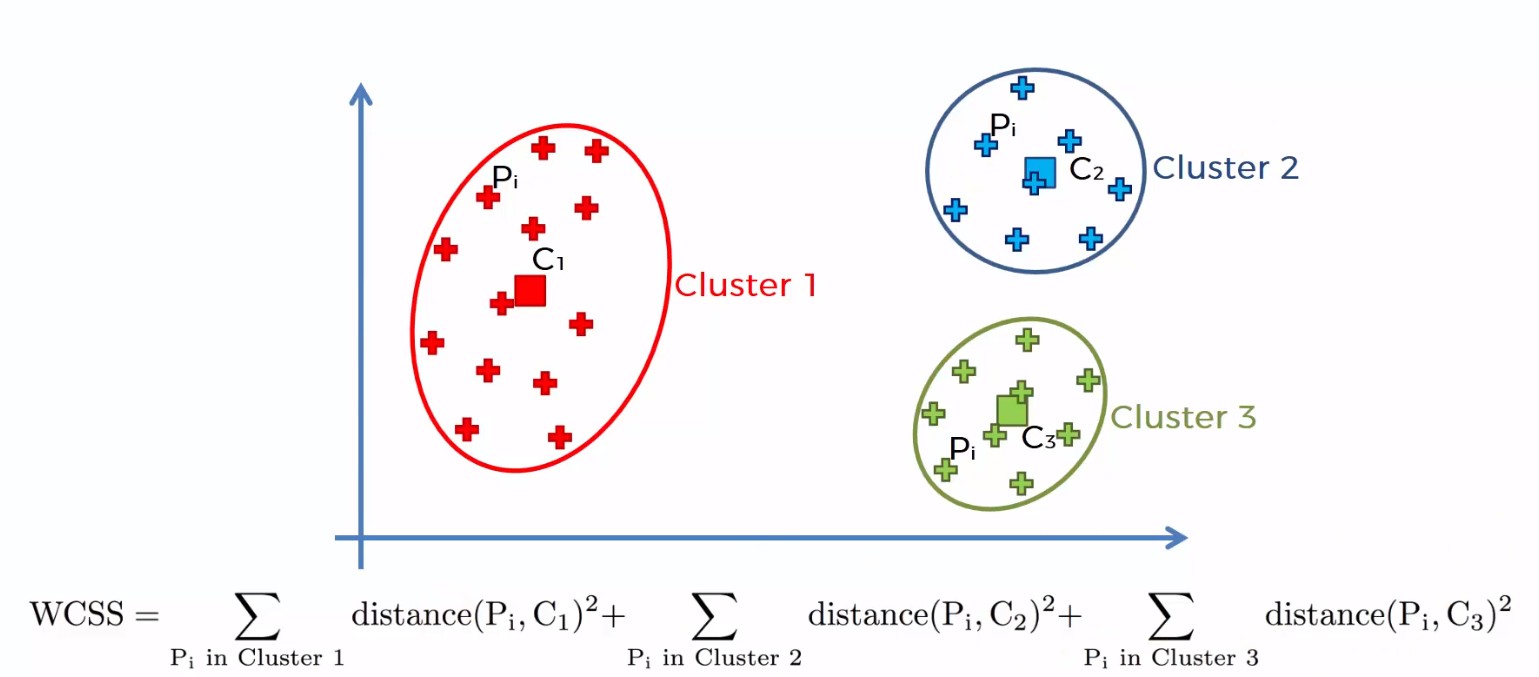
La somma delle distanze al quadrato tra i singoli punti e il baricentro in ciascun gruppo, seguito dalla somma delle distanze al quadrato per tutti i cluster, Si chiama "Somma dei quadrati all'interno del cluster". Sarai in grado di capirlo con l'aiuto dei seguenti passaggi.
1) Calcola la distanza tra il baricentro e ogni punto del gruppo, quadrato e poi aggiungi le distanze al quadrato per tutti i punti nel gruppo.
2) Calcola allo stesso modo la somma dei quadrati delle distanze dei restanti gruppi.
3) Finalmente, sommare tutte le somme dei gruppi per ottenere il valore della "Somma dei quadrati all'interno del gruppo" come mostrato nella figura seguente.
Il “totale all'interno della somma dei quadrati” comienza a disminuir a misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... que aumenta el valor de k. Il grafico tra il numero di cluster e il totale all'interno della somma dei quadrati è mostrato nella figura seguente. Il numero ottimale di cluster, o il valore corretto di k, è il punto in cui il valore inizia a diminuire lentamente; questo è noto come “punto del gomito”, e il punto del gomito nel grafico seguente è k = 4. Il “Metodo del gomito” prende il nome dalla somiglianza del grafico al gomito, e il punto ottimale per “K” è il punto del gomito .
Vantaggi del clustering di mezzi k
1) I dati taggati non sono obbligatori. Poiché molti dati del mondo reale non sono etichettati, di conseguenza, sono frequentemente utilizzati in una varietà di affermazioni di problemi del mondo reale.
2) È facile da implementare.
3) Può gestire enormi quantità di dati.
4) Quando i dati sono grandi, lavorare più velocemente del raggruppamento gerarchico (per k piccoli).
Svantaggi del clustering di mezzi K
1) Il valore di K deve essere selezionato manualmente tramite il tasto “metodo del gomito”.
2) La presenza di valori anomali avrebbe un impatto negativo sul raggruppamento. Di conseguenza, i valori anomali devono essere rimossi prima di utilizzare il raggruppamento k-means.
3) I gruppi non si intersecano; un punto può appartenere solo a un gruppo alla volta. A causa della mancanza di sovrapposizione, alcuni punti sono inseriti in gruppi sbagliati.
K significa raggruppamento con R
- Importeremo le seguenti librerie nel nostro lavoro.
biblioteca (intercalazione)
biblioteca (ggplot2)
biblioteca (dplyr)
- Lavoreremo con i dati dell'iride, contenente tre classi: “Iris-setosa”, “Iris-versicolor” e “Iris-verginica”.
dati <- leggi.csv ("iride.csv", intestazione = T)
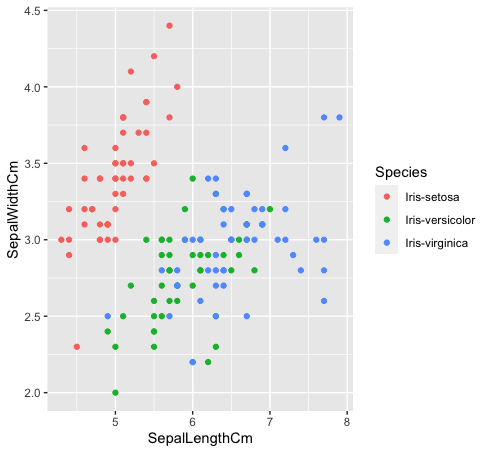
- Vediamo come queste tre classi sono correlate tra loro. Le specie “Iris-versicolor” (verde) e “Iris-verginica” (blu) non sono linearmente separabili. Come puoi vedere nel grafico qui sotto, si mescolano.
dati%>% ggplot (aes (SepaloLunghezzaCm, SepaloLarghezzaCm, colore = specie)) +
geom_point ()
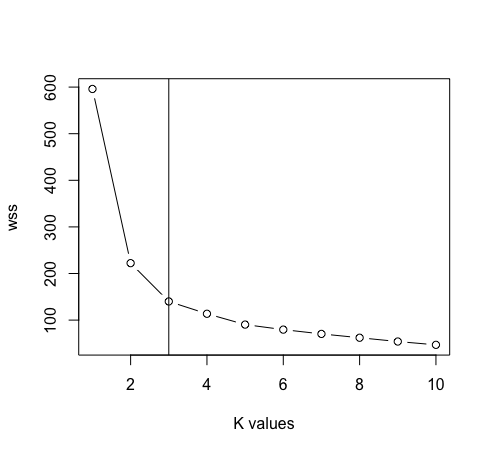
- Dopo aver rimosso la colonna delle specie dai dati. Ora useremo il grafico del metodo del gomito tra “Somma dei quadrati all'interno del cluster” e “valori K” per determinare il valore appropriato di k. K = 3 è il miglior valore per k in questo caso (Nota: ci sono 3 classi nei dati originali dell'iride, che garantisce la precisione del valore di k).
dati <- dati[, -5]
massimo <- 10
scala <- scala (dati)
wss <- sapply (1: massimo, funzione (K) {km significa (scala, K, nstart = 50, iter.max = 15) $ tot.all'interno})
complotto (1: max, wss, tipo = “B”, xlab = “valori k”)
abline (v = 3)
- Per k = 3, aplique el algoritmo de raggruppamentoIl "raggruppamento" È un concetto che si riferisce all'organizzazione di elementi o individui in gruppi con caratteristiche o obiettivi comuni. Questo processo viene utilizzato in varie discipline, compresa la psicologia, Educazione e biologia, per facilitare l'analisi e la comprensione di comportamenti o fenomeni. In ambito educativo, ad esempio, Il raggruppamento può migliorare l'interazione e l'apprendimento tra gli studenti incoraggiando il lavoro.. de K-medias. L'approccio K-means clustering spiega il 71,5% della variabilità dei dati in questo caso.
km <- kmedias (dati[,1:2], k = 3, iter.max = 50)
km
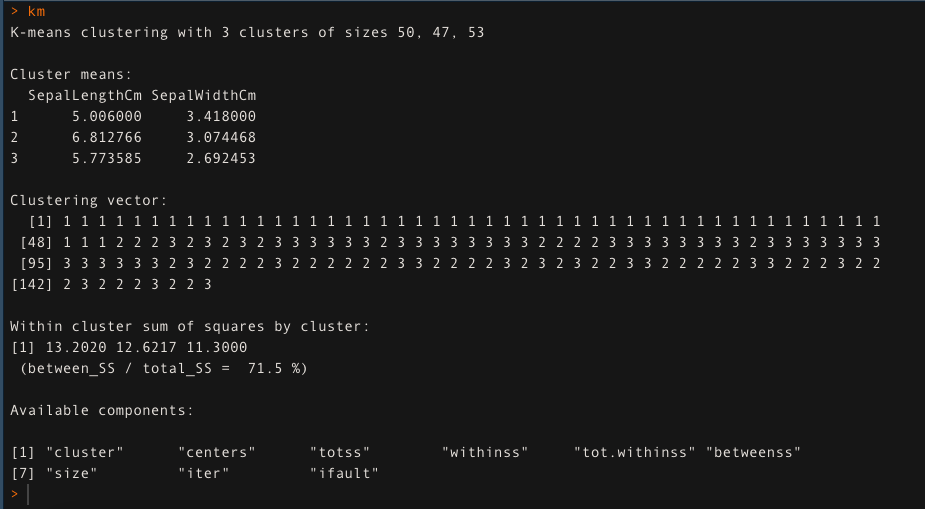
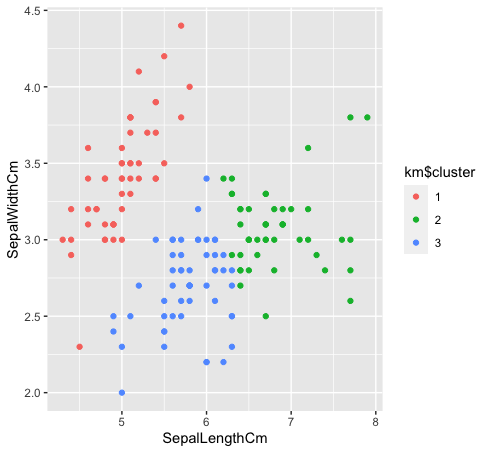
- Vediamo come le tre classi sono raggruppate raggruppando k-mezzi. K-significa che il clustering non creerà cluster sovrapposti, come sappiamo tutti. Poiché la specie “verde” e “blu” non sono linearmente separabili nei dati originali, il raggruppamento di k-mean non ha potuto catturarlo perché ha gruppi ridotti.
km $ grappolo <- come.fattore (km $ grappolo)
dati%>% ggplot (aes (SepaloLunghezzaCm, SepaloLarghezzaCm, colore = km $ grappolo)) +
geom_point ()
Un articolo di ~
Shivam Sharma.
Il supporto mostrato in questo articolo sull'algoritmo di raggruppamento K-Means non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.
