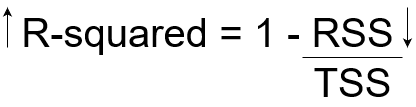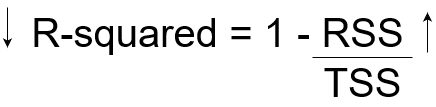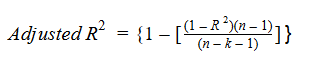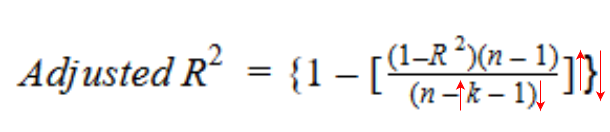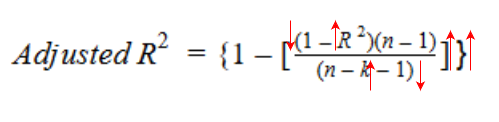Panoramica
- Comprendere il concetto di R al quadrato e R al quadrato rettificato
- Impara le principali differenze tra R-quadrato e R-quadrato aggiustato
introduzione
Quando ho iniziato il mio viaggio nella scienza dei dati, il primo algoritmo che ho esplorato è stato la regressione lineare. Dopo aver compreso i concetti di regressione lineare e come funziona l'algoritmo, Ero davvero entusiasta di usarlo e fare previsioni su una dichiarazione di problema. Sono sicuro che molti di voi avrebbero fatto lo stesso. Ma una volta che abbiamo previsto i valori, Qual è il prossimo?
Poi arriva la parte difficile. Una volta che abbiamo costruito il nostro modello, il passo successivo è stato valutare le loro prestazioni. Va da sé che il compito della valutazione del modello è fondamentale e mette in evidenza le carenze del nostro modello.. Scegli il più adatto Metrica di valutazione è un compito cruciale. E ho trovato due parametri importanti: R-quadrato e R-quadrato aggiustati oltre a MAE / MSE / RMSE. Qual è la differenza tra questi due? Quale dovrei usare??
R al quadrato e R al quadrato aggiustato sono due di queste metriche di valutazione che inizialmente possono sembrare confuse a qualsiasi aspirante scienza dei dati.. Poiché entrambi sono estremamente importanti per valutare i problemi di regressione, li capiremo e li confronteremo in profondità. entrambi hanno i loro pro e contro, di cui parleremo in dettaglio in questo articolo.
Nota: Per capire R-quadrato e R-quadrato aggiustato, deve avere una buona conoscenza della regressione lineare. Scopri il nostro corso gratuito –
Sommario
- Somma residua dei quadrati
- Comprensione della statistica R-quadrato
- Problemi con la statistica R-quadrato
- Statistica R-quadrato rettificato
Somma residua dei quadrati
Per comprendere chiaramente i concetti, affronteremo un semplice problema di regressione. Qui, stiamo cercando di prevedere i "voti ottenuti"’ a seconda della quantità di "tempo trascorso a studiare". il tempo metereologico trascorso a studiare sarà nostro variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... Indipendente e il marchi di fabbrica compiuto nel test è nostro dipendente oh variabile di destinazione.
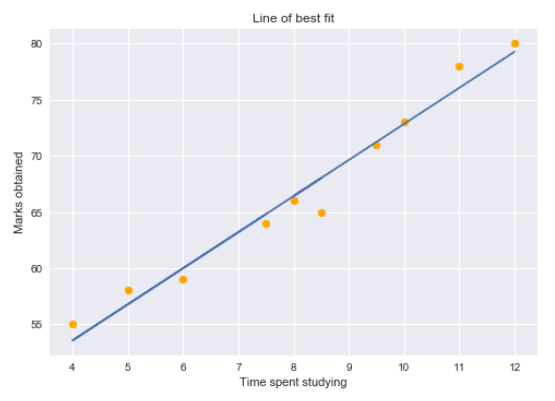
Possiamo tracciare un semplice grafico di regressione per visualizzare questi dati.
I punti gialli rappresentano i punti dati e la linea blu è la nostra linea di regressione prevista. Come potete vedere, il nostro modello di regressione non prevede perfettamente tutti i punti dati. Quindi, Come valutiamo le previsioni della retta di regressione utilizzando i dati?? Bene, potremmo iniziare determinando i valori residui per i punti dati.
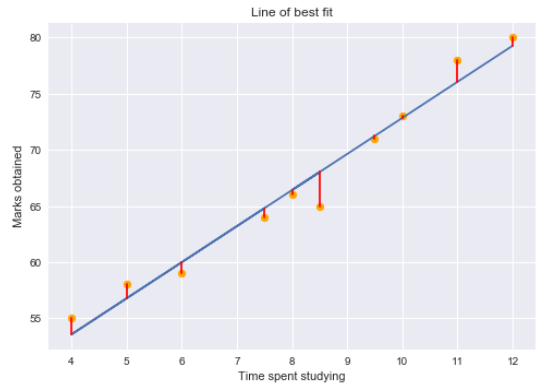
Residuo per un punto nei dati è la differenza tra il valore effettivo e il valore previsto dal nostro modello di regressione lineare.
I grafici residui ci dicono se il modello di regressione è giusto per i dati o no. In realtà, è un presupposto del modello di regressione che non vi sia alcun andamento nei grafici residui. Per studiare in dettaglio le ipotesi di regressione lineare, suggerisco di passare questo grande artitolo!
Utilizzo dei valori residui, possiamo determinare la somma dei quadrati dei residui detta anche Somma residua dei quadrati o RSS.
Più basso è il valore RSS, migliori sono le previsioni del modello. Oppure possiamo dire che una linea di regressione è una linea che si adatta meglio se si riduce al minimo il valore di RSS. Ma c'è un difetto in questo: RSS è una statistica variante di ridimensionamento. Poiché RSS è la somma della differenza al quadrato tra il valore effettivo e quello previsto, il valore dipende dalla scala della variabile target.
Esempio:
Considera che la tua variabile target è il reddito generato dalla vendita di un prodotto. I residui dipenderebbero dalla scala di questo obiettivo. Se si tiene conto della scala del reddito “Centinaia di rupie” (vale a dire, l'obiettivo sarebbe 1, 2, 3, eccetera.), quindi potremmo ottenere un RSS di circa 0,54 (parlando per ipotesi).
Ma se la variabile del reddito target è stata presa in considerazione “rupie” (vale a dire, l'obiettivo sarebbe 100, 200, 300, eccetera.), quindi potremmo ottenere un RSS like più alto 5400. Anche se i dati non cambiano, il valore di RSS varia. secondo la scala oggettiva. Ciò rende difficile giudicare quale potrebbe essere un buon valore RSS..
Quindi, Possiamo fornire una statistica migliore che sia invariante di scala?? È qui che entra in gioco R-square..
Comprensione della statistica R-quadrato
La statistica R-quadrato o coefficiente di determinazione è una statistica invariante di scala che fornisce la proporzione di variazione nella variabile target spiegata dal modello di regressione lineare..
Questo può sembrare un po' complicato., quindi fammi scomporre qui. Per determinare la proporzione di variazione target spiegata dal modello, dobbiamo prima determinare quanto segue:
-
Somma totale dei quadrati
La variazione totale della variabile target è la somma dei quadrati della differenza tra i valori reali e la loro media.
TSS o somma totale dei quadrati dà la variazione totale in Y. Possiamo vedere che è molto simile alla varianza di Y. Mentre la varianza è la media delle somme al quadrato della differenza tra i valori reali e i punti dati, TSS è il totale delle somme al quadrato.
Ora che conosciamo la variazione totale nella variabile target, Come determiniamo la proporzione di questa variazione spiegata dal nostro modello?? Torniamo a RSS.
-
Somma residua dei quadrati
Come abbiamo commentato prima, RSS ci dà il quadrato totale della distanza dei punti reali dalla retta di regressione. Ma se ci concentriamo su un singolo residuo, possiamo dire che è la distanza che non viene catturata dalla retta di regressione. Perciò, RSS nel suo insieme ci dà la variazione nella variabile target che è non spiegato dal nostro modello.
-
Calcola R-quadrato
Ora, se TSS ci dà la variazione totale in Y, e RSS ci dà la variazione in Y non spiegata da X, poi TSS-RSS ci fornisce la variazione in Y spiegata dal nostro modello! Possiamo semplicemente dividere questo valore per TSS per ottenere la proporzione di variazione in Y spiegata dal modello. E questo nostro Statistica R-quadrato!
R-quadrato = (TSS-RSS) / TSS
= Variazione spiegata / Variazione totale
= 1 – Variazione inspiegabile / Variazione totale
Quindi, R al quadrato fornisce il grado di variabilità nella variabile target che è spiegato dal modello o dalle variabili indipendenti. Se questo valore è 0,7, significa che le variabili indipendenti spiegano il 70% della variazione della variabile target.
Il valore di R al quadrato è sempre compreso tra 0 e 1. Un valore R quadrato più alto indica una maggiore quantità di variabilità spiegata dal nostro modello e viceversa..
Se avessimo un valore RSS davvero basso, significherebbe che la retta di regressione era molto vicina ai punti reali. Ciò significa che le variabili indipendenti spiegano la maggior parte della variazione nella variabile target.. In quel caso, avremmo un valore R-quadro davvero alto.
al contrario, se avessimo un valore RSS davvero alto, significherebbe che la retta di regressione sarebbe molto lontana dai punti reali. Perciò, le variabili indipendenti non riescono a spiegare la maggior parte della variazione nella variabile target. Questo ci darebbe un valore R-quadro davvero basso.
Quindi, questo spiega perché il valore R-quadrato ci dà la variazione della variabile target data dalla variazione delle variabili indipendenti.
Problemi con la statistica R-quadrato
La statistica R al quadrato non è perfetta. Infatti, soffre di un grave difetto. Il suo valore non diminuisce mai, non importa quante variabili aggiungiamo al nostro modello di regressione. Vale a dire, anche se aggiungiamo variabili ridondanti ai dati, il valore di R al quadrato non diminuisce. O rimane lo stesso o aumenta con l'aggiunta di nuove variabili indipendenti. Questo chiaramente non ha senso perché alcune delle variabili indipendenti potrebbero non essere utili nel determinare la variabile target.. R-quadrato aggiustato si occupa di questo problema.
Statistica R-quadrato rettificato
L'R-quadrato aggiustato tiene conto del numero di variabili indipendenti utilizzate per prevedere la variabile target.. Così facendo, possiamo determinare se l'aggiunta di nuove variabili al modello aumenta effettivamente l'adattamento del modello.
Diamo un'occhiata alla formula R-quadrato modificata per capire meglio come funziona..
Qui,
- Nord rappresenta il numero di punti dati nel nostro set di dati
- K rappresenta il numero di variabili indipendenti, e
- R rappresenta i valori R al quadrato determinati dal modello.
Quindi, se R-quadrato non aumenta significativamente con l'aggiunta di una nuova variabile indipendente, quindi il valore R al quadrato regolato diminuirà effettivamente.
In secondo luogo, se sommando la nuova variabile indipendente vediamo un aumento significativo del valore di R al quadrato, quindi aumenterà anche il valore R al quadrato regolato.
Possiamo vedere la differenza tra i valori R al quadrato e R al quadrato aggiustato se aggiungiamo una variabile indipendente casuale al nostro modello.
Come potete vedere, l'aggiunta di una variabile indipendente casuale non ha aiutato a spiegare la variazione nella variabile target. Il nostro valore R al quadrato rimane lo stesso. Perciò, ci dà una falsa indicazione che questa variabile potrebbe essere utile per prevedere l'output. tuttavia, il valore R al quadrato regolato è diminuito, che ha indicato che questa nuova variabile non sta effettivamente catturando la tendenza nella variabile target.
Chiaramente, è meglio usare R-quadrato aggiustato quando ci sono più variabili nel modello di regressione. Questo ci permetterebbe di confrontare modelli con diversi numeri di variabili indipendenti.
Note finali
In questo articolo, analizziamo cos'è la statistica R-quadrato e dove fallisce. Diamo anche un'occhiata a R al quadrato rettificato.
Auspicabilmente, questo gli ha dato una migliore comprensione delle cose. Ora puoi determinare saggiamente quali variabili indipendenti sono utili per prevedere l'esito del tuo problema di regressione..
Per saperne di più su altre metriche di valutazione, Suggerisco di dare un'occhiata alle seguenti fantastiche risorse: