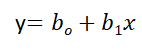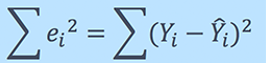Regressione lineare | Introduzione alla regressione lineare per la scienza dei dati

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati

introduzione

Se stai leggendo questo articolo, Immagino che tu sia già nel mondo della scienza dei dati e hai un'idea sull'apprendimento automatico. Se non è così, Nessun problema. Inizierò con le terminologie di base che è necessario conoscere prima di comprendere l'argomento principale della discussione, vale a dire, regressione lineare.

Questo articolo tratterà tutto ciò che devi sapere sulla regressione lineare., il primo algoritmo di apprendimento automatico della scienza dei dati.

Sommario

1. Breve introduzione all'apprendimento automatico e ai suoi tipi
2. Comprensione della regressione lineare
3. Ipotesi di regressione lineare.
4. Come affrontare la violazione dei presupposti
5. Metriche di valutazione per problemi di regressione

Introduzione all'apprendimento automatico

L'apprendimento automatico è una branca dell'intelligenza artificiale (LUI) focalizzato sulla creazione di applicazioni che apprendono dai dati e migliorano la precisione nel tempo senza essere programmati per farlo.

Tipi di apprendimento automatico:

Apprendimento automatico supervisionato: È una tecnica ML in cui i modelli vengono addestrati con dati etichettati, vale a dire, se proporciona una variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... de salida en este tipo de problemas. Qui, i modelli trovano la funzione di mappatura per mappare le variabili di input alla variabile o alle etichette di output.
Regressione e classificazione I problemi fanno parte dell'apprendimento automatico supervisionato.

Apprendimento automatico senza supervisione: È la tecnica in cui i modelli non ricevono i dati etichettati e devono trovare i modelli e la struttura nei dati per conoscere i dati.
Raggruppamento e associazione Gli algoritmi fanno parte del ML non supervisionato.

Comprensione della regressione lineare

Nelle parole più semplici Regressione lineare è il modello di apprendimento automatico supervisionato in cui il modello trova la linea lineare di miglior adattamento tra la variabile indipendente e quella dipendente vale a dire, trovare la relazione lineare tra le variabili dipendenti e indipendenti.

La regressione lineare è di due tipi: Semplice e multiplo. Regressione lineare semplice è dove è presente una sola variabile indipendente e il modello deve trovare la sua relazione lineare con la variabile dipendente

Nel frattempo Regressione lineare multipla c'è più di una variabile indipendente per il modello per trovare la relazione.

Equazione di regressione lineare semplice, dove b_oh è l'intersezione, B₁ è coefficiente o pendenza, x è la variabile indipendente e y è la variabile dipendente.

Equazione di regressione lineare multipla, dove boh è l'intersezione, B₁,B₂,B₃,B₄…,B_Nord sono coefficienti o pendenze delle variabili indipendenti x₁,X₂,X₃,X₄…,X_Nord e y è la variabile dipendente.

L'obiettivo principale di un modello di regressione lineare è trovare la linea lineare che meglio si adatta e i valori ottimali di intersezione e coefficienti in un modo che minimizzi l'errore.
L'errore è la differenza tra il valore effettivo e il valore previsto e l'obiettivo è ridurre questa differenza.

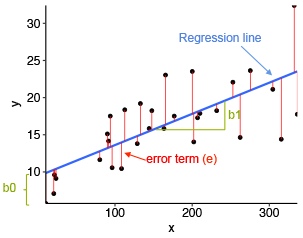
Capiamolo con l'aiuto di un diagramma.

Fonte immagine: strumenti statistici per l'analisi dei dati ad alte prestazioni

Nello schema sopra,

• x è la nostra variabile dipendente che viene tracciata sull'asse x e y è la variabile dipendente che viene tracciata sull'asse y.
• I punti neri sono i punti dati, vale a dire, i valori reali.
• B_oh è l'intersezione che è 10 e B₁ è la pendenza della variabile x.
• La linea blu è la linea di miglior adattamento prevista dal modello, vale a dire, i valori previsti sono sulla linea blu.

La distanza verticale tra il punto dati e la linea di regressione è nota come errore o residuo. Ogni punto dati ha un resto e la somma di tutte le differenze è nota come la somma dei residui / errori.

Approccio matematico:

Residuo / Errore = Valori effettivi – Valori previsti

Somma dei residui / errori = Somma (valori effettivi previsti)

Quadrato della somma dei residui / errori = (Somma (valori effettivi previsti))²

vale a dire

Per una profonda comprensione della matematica alla base della regressione lineare, vedi allegato spiegazione video.

Ipotesi di regressione lineare

Le ipotesi di base della regressione lineare sono le seguenti:

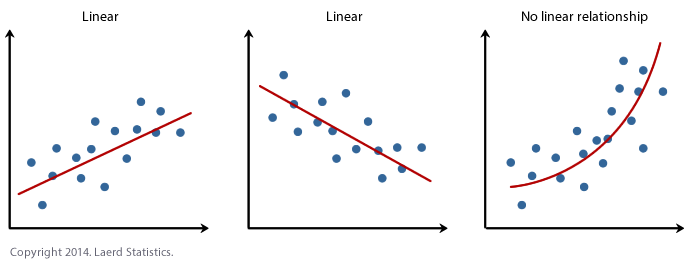
1. Linearità: Stabilisce che la variabile dipendente Y deve essere linearmente correlata alle variabili indipendenti. Questa ipotesi può essere verificata disegnando un diagramma di dispersione tra entrambe le variabili.

2. Normale: Le variabili X e Y devono avere una distribuzione normale. È possibile utilizzare gli istogrammi, Grafici KDE e grafici QQ per verificare l'ipotesi di normalità.

Vedi il mio blog allegato per una spiegazione dettagliata su come controllare la normalità e trasformare le variabili che violano il presupposto.

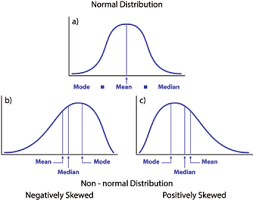
Fonte: https://heljves.com/gallery/vol_1_issue_1_2019_8.pdf

3. omoschedasticità: La varianza dei termini di errore deve essere costante, vale a dire, la dispersione dei residui deve essere costante per tutti i valori di X. Questa ipotesi può essere verificata disegnando un grafico residuo. Se il presupposto viene violato, i punti formeranno una forma ad imbuto, altrimenti saranno costanti.

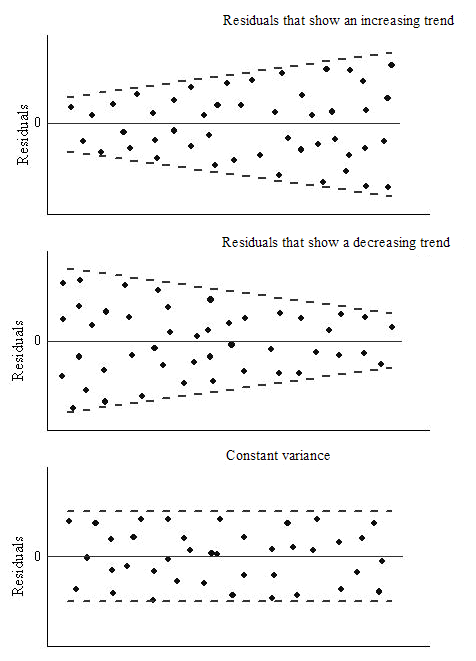
Fonte: OriginLab

4. Indipendenza / Nessuna multicollinearità: Le variabili devono essere indipendenti l'una dall'altra, vale a dire, non dovrebbe esserci alcuna correlazione tra le variabili indipendenti. Per verificare l'ipotesi, possiamo usare una matrice di correlazione o un punteggio VIF. Se il punteggio VIF è maggiore di 5, le variabili sono altamente correlate.

Nell'immagine qui sotto, esiste un'elevata correlazione tra le variabili x5 e x6.

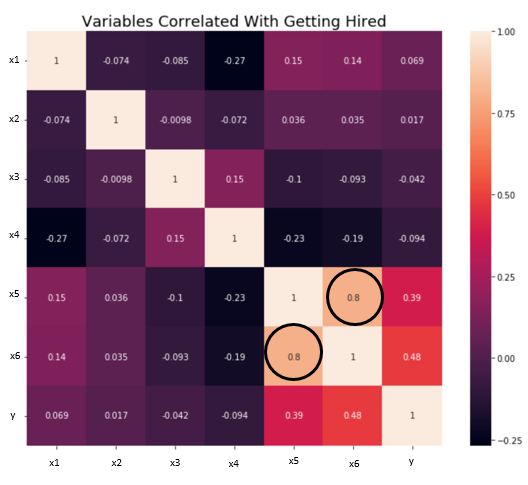
Fonte: verso la scienza dei dati

5. il i termini di errore dovrebbero essere distribuiti normalmente. I grafici QQ e gli istogrammi possono essere utilizzati per controllare la distribuzione dei termini di errore.

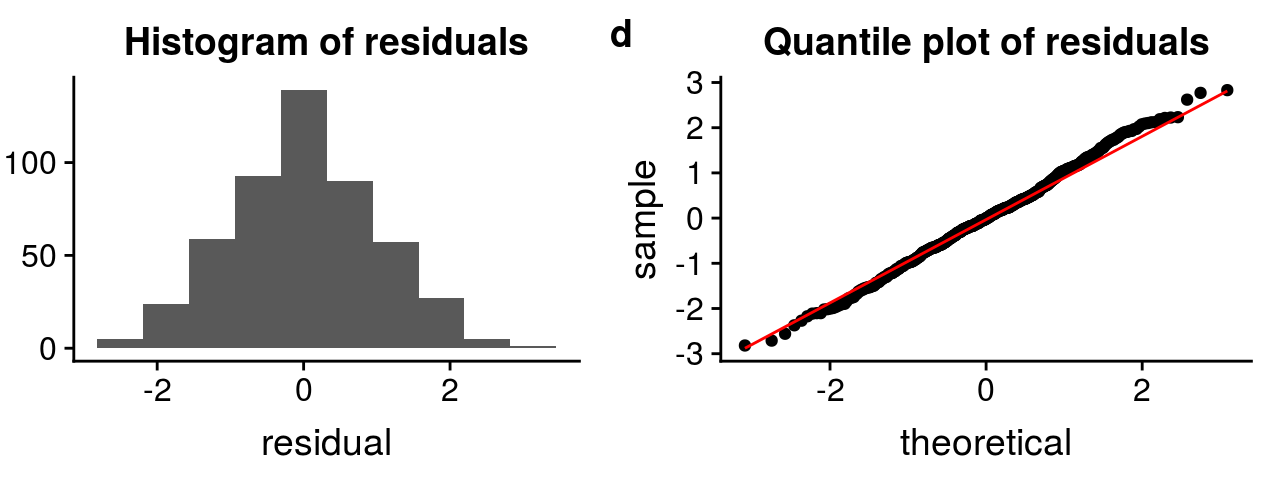
Fonte: http://rstudio-pubs-static.s3.amazonaws.com

6. Nessuna autocorrelazione: I termini di errore devono essere indipendenti l'uno dall'altro. L'autocorrelazione può essere testata utilizzando il test di Durbin Watson. L'ipotesi nulla presuppone che non ci sia autocorrelazione. Il valore del test è compreso tra 0 e 4. Se il valore del test è 2, nessuna autocorrelazione.

Fonte: itfeature.com

Come affrontare la violazione di uno qualsiasi dei presupposti

La violazione delle assunzioni porta ad una diminuzione della precisione del modello, quindi le previsioni non sono accurate e anche l'errore è alto.
Ad esempio, se viene violato il presupposto di indipendenza, la relazione tra variabile indipendente e dipendente non può essere determinata con precisione.

Esistono vari metodi e tecniche disponibili per affrontare la violazione dei presupposti. Analizziamone alcune di seguito.

Violazione del presupposto di normalità delle variabili o dei termini di errore

Per trattare questo problema, possiamo trasformare le variabili nella distribuzione normale usando varie funzioni di trasformazione come la trasformazione logaritmica, Trasformazione reciproca Box-Cox.
Tutte le funzioni sono discusse in questo mio articolo: Come passare alla distribuzione normale

Violazione del presupposto di multicollinearità

Può essere trattato da:

• Fare niente (se non ci sono grandi differenze di precisione)
• Eliminazione di alcune delle variabili indipendenti altamente correlate.
• Derivare una nuova caratteristica combinando linearmente le variabili indipendenti, come aggiungerli o eseguire qualche operazione matematica.
• Esecuzione di un'analisi progettata per variabili altamente correlate, come l'analisi dei componenti principali.

Metriche di valutazione per l'analisi di regressione

Per comprendere le prestazioni del modello di regressione, è necessaria una valutazione del modello. Alcune delle metriche di valutazione utilizzate per l'analisi di regressione sono:

1. R quadrato o coefficiente di determinazione: La metrica più utilizzata per la valutazione del modello nell'analisi di regressione è R al quadrato. Può essere definito come un rapporto tra variazione e variazione totale. Il valore di R al quadrato è compreso tra 0 e 1, il più vicino a 1, migliore è il modello.

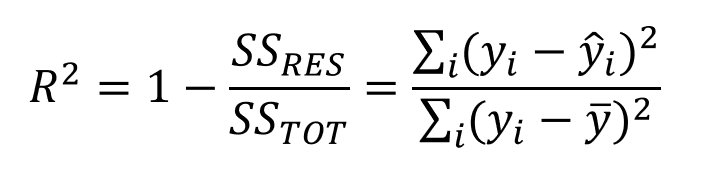
Fonte: medium.datadriveninvestor.com

dove SSRES è la somma residua dei quadrati e SSOT è la somma totale dei quadrati

2. R quadrato montato: È il miglioramento di R al quadrato. Il problema / inconveniente de R2 es que a misuraIl "misura" È un concetto fondamentale in diverse discipline, che si riferisce al processo di quantificazione delle caratteristiche o delle grandezze degli oggetti, fenomeni o situazioni. In matematica, Utilizzato per determinare le lunghezze, Aree e volumi, mentre nelle scienze sociali può riferirsi alla valutazione di variabili qualitative e quantitative. L'accuratezza della misurazione è fondamentale per ottenere risultati affidabili e validi in qualsiasi ricerca o applicazione pratica.... que aumentan las características, aumenta anche il valore di R2, che dà l'illusione di un buon modello. Quindi, R2 aggiustato risolve il problema R2. Considera solo le caratteristiche importanti per il modello e mostra l'effettivo miglioramento del modello.
R2 aggiustato è sempre minore di R2.

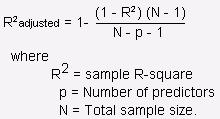
Fonte: stats.stackexchange.com

3. Root errore quadratico medio (MSE): Un'altra metrica comune per la valutazione è la radice dell'errore quadratico medio., che è la media della differenza al quadrato dei valori reali rispetto a quelli previsti.

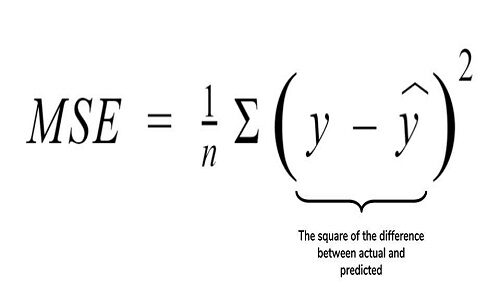
Fonte: cppsecrets.com

4. Root errore quadratico medio (RMSE): È la radice di MSE, vale a dire, la radice della differenza media dei valori effettivi e previsti. RMSE penalizza i grandi errori, mentre MSE no.

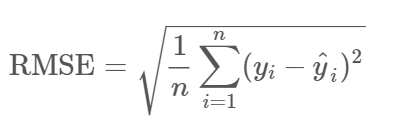
Fonte: community.qlik.com

Note finali

Abbiamo coperto la maggior parte dei concetti del modello di regressione su questo blog. Se vuoi approfondire la matematica dietro il modello, vedi i link allegati al blog.

Per favore, sentiti libero di connetterti con me su LinkedIn e condividi il tuo prezioso contributo. Per favore, dai un'occhiata agli altri miei articoli qui.

Circa l'autore :

Soy Deepanshi Dhingra, Attualmente lavoro come ricercatore di data science e ho un background in analisi, analisi esplorativa dei dati, aprendizaje automático y apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute....

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati

Imparentato