introduzione
Tutti i modelli sono sbagliati, ma alcuni sono utili – George Box
L'analisi di regressione segna il primo passo nella modellazione predittiva. Decisamente, è abbastanza facile da implementare. Né la sua sintassi né i suoi parametri creano alcun tipo di confusione. Ma, basta eseguire solo una riga di codice, non risolve lo scopo. Non solo guardando i valori R² o MSE. La regressione dice molto di più!!
un R, rendimenti dell'analisi di regressione 4 grafica usando plot(model_name) funzione. Ciascuno dei grafici fornisce informazioni significative o piuttosto una storia interessante sui dati. purtroppo, molti dei principianti non riescono a decifrare le informazioni o non si preoccupano di cosa dicono queste trame. Una volta compresi questi grafici, puoi apportare un miglioramento significativo al tuo modello di regressione.
Per migliorare il modello, devi anche comprendere le ipotesi di regressione e i modi per correggerle quando vengono violate.
In questo articolo, Ho spiegato le importanti ipotesi di regressione e grafici (con correzioni e soluzioni) per aiutarti a capire il concetto di regressione in modo più dettagliato. Come sopra, con questa conoscenza puoi apportare miglioramenti drastici ai tuoi modelli.
Nota: Per capire questi grafici, devi conoscere le basi dell'analisi di regressione. Se sei completamente nuovo ad esso, puoi iniziare da qui. Dopo, continua con questo articolo.
Ipotesi di regressione
La regressione è un approccio parametrico. ‘Parametrico’ significa che fai supposizioni sui dati per scopi di analisi. A causa del suo lato parametrico, la regressione è di natura restrittiva. Non funziona bene con set di dati che non soddisfano le tue ipotesi. Perciò, per un'analisi di regressione di successo, è essenziale convalidare queste ipotesi.
Quindi, Come verificheresti? (confermerebbe) se un set di dati segue tutte le ipotesi di regressione? Controllalo usando i grafici di regressione (spiegato di seguito) insieme a qualche prova statistica.
Diamo un'occhiata alle assunzioni importanti nell'analisi di regressione:
- Ci deve essere una relazione lineare e additiva tra la variabile dipendente (Rispondere) e la variabile indipendente (predittore). Una relazione lineare suggerisce che un cambiamento nella risposta Y dovuto a un cambiamento di un'unità in X¹ è costante, indipendentemente dal valore di X¹. Una relazione additiva suggerisce che l'effetto di X¹ su Y è indipendente da altre variabili.
- Non dovrebbe esserci alcuna correlazione tra i termini residui (errore). L'assenza di questo fenomeno è nota come autocorrelazione..
- Le variabili indipendenti non devono essere correlate. L'assenza di questo fenomeno è nota come multicollinearità..
- I termini di errore devono avere una varianza costante. Questo fenomeno è noto come omoschedasticità.. La presenza di varianza non costante si riferisce all'eteroschedasticità.
- I termini di errore dovrebbero essere distribuiti normalmente.
E se questi presupposti venissero violati??
Analizziamo ipotesi specifiche e impariamo a conoscere i tuoi risultati (se vengono violentate):
1. Lineare e additivo: Se si adatta un modello lineare a un set di dati non lineare e non additivo, l'algoritmo di regressione non catturerebbe matematicamente la tendenza, che risulterebbe in un modello inefficiente. Cosa c'è di più, questo si tradurrà in previsioni errate in un set di dati invisibile.
Come controllare: Cerca i grafici del valore residuo rispetto a quello aggiustato (spiegato di seguito). Cosa c'è di più, può includere termini polinomiali (X, X², X³) nel tuo modello per catturare l'effetto non lineare.
2. Autocorrelazione: La presenza di correlazione in termini di errore riduce drasticamente la precisione del modello. Questo di solito accade nei modelli di serie temporali in cui l'istante successivo dipende dall'istante precedente. Se i termini di errore sono correlati, gli errori standard stimati tendono a sottovalutare il vero errore standard.
Se questo accade, rende gli intervalli di confidenza e gli intervalli di previsione più stretti. Un intervallo di confidenza più stretto significa che un intervallo di confidenza di 95% avrebbe una probabilità minore di 0,95 contenere il valore reale dei coefficienti. Comprendiamo gli intervalli di previsione ristretti con un esempio:
Ad esempio, il coefficiente dei minimi quadrati di X¹ è 15.02 e il suo errore standard è 2.08 (nessuna autocorrelazione). Ma in presenza di autocorrelazione, l'errore standard si riduce a 1,20. Di conseguenza, l'intervallo di previsione è ridotto a (13.82, 16.22) a partire dal (12.94, 17.10).
Cosa c'è di più, errori standard inferiori renderebbero i valori p associati inferiori a quelli effettivi. Questo ci farà concludere erroneamente che un parametro è statisticamente significativo..
Come controllare: Consulta la statistica Durbin-Watson (DW). Deve essere tra 0 e 4. Se DW = 2, non implica autocorrelazione, 0 <DW <2 implica un'autocorrelazione positiva mentre 2 <DW <4 indica un'autocorrelazione negativa. Cosa c'è di più, puoi visualizzare il grafico residuo rispetto al tempo e cercare il modello stagionale o correlato nei residui.
3. Multicollinearità: Questo fenomeno esiste quando si scopre che le variabili indipendenti hanno una correlazione moderata o alta. In un modello con variabili correlate, diventa un compito difficile scoprire la vera relazione di un predittore con una variabile di risposta. In altre parole, difficile capire quale variabile contribuisce effettivamente a prevedere la variabile di risposta.
Un altro punto, con la presenza di predittori correlati, gli errori standard tendono ad aumentare. E, con grandi errori standard, l'intervallo di confidenza diventa più ampio, portando a stime meno accurate dei parametri di pendenza.
Cosa c'è di più, quando i predittori sono correlati, il coefficiente di regressione stimato di una variabile correlata dipende da quali altri predittori sono disponibili nel modello. Se questo accade, finirai con una conclusione errata che una variabile influisce fortemente / debolmente alla variabile target. dato che, anche se rimuovi una variabile correlata dal modello, i coefficienti di regressione stimati cambierebbero. Questo non è buono!
Come controllare: È possibile utilizzare il grafico a dispersione per visualizzare l'effetto di correlazione tra le variabili. Cosa c'è di più, puoi anche usare il fattore VIF. Il valore di VIF = 10 implica una grave multicollinearità. Soprattutto, una tabella di correlazione dovrebbe anche risolvere lo scopo.
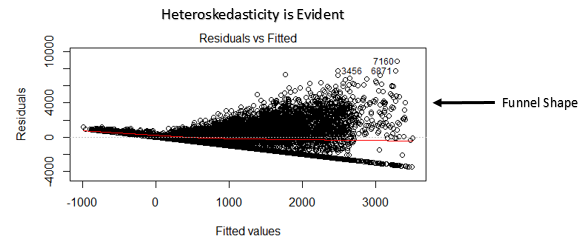
4. eteroschedasticità: La presenza di varianza non costante nei termini di errore determina eteroschedasticità. In genere, la varianza non costante si verifica in presenza di valori anomali o valori di leva estremi. Questi valori sembrano avere troppo peso, quindi influenzano in modo sproporzionato le prestazioni del modello. Quando si verifica questo fenomeno, l'intervallo di confidenza per la previsione fuori campione tende ad essere irrealisticamente ampio o stretto.
Come controllare: Puoi vedere il grafico dei residui rispetto al montaggio. Se c'è eteroschedasticità, il grafico visualizzerà un motivo a forma di imbuto (mostrato nella prossima sezione). Cosa c'è di più, puoi usare il test di Breusch-Pagan / cucinare – Weisberg o il test generale di White per rilevare questo fenomeno.
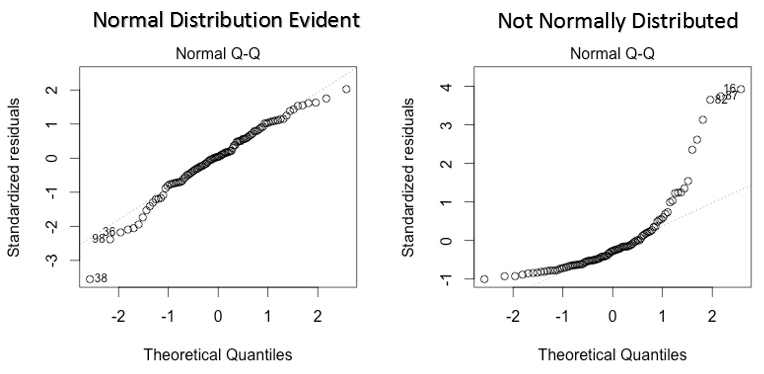
5. Distribuzione normale dei termini di errore: Se i termini di errore non sono distribuiti normalmente, gli intervalli di confidenza possono diventare troppo ampi o troppo stretti. Una volta che l'intervallo di confidenza diventa instabile, la stima dei coefficienti basata sulla minimizzazione dei minimi quadrati è difficile. La presenza di una distribuzione anormale suggerisce che ci sono alcuni punti dati insoliti che devono essere studiati da vicino per creare un modello migliore..
Come controllare: Puoi vedere il grafico QQ (mostrato sotto). Puoi anche eseguire test statistici per la normalità come il test di Kolmogorov-Smirnov., il test di Shapiro-Wilk.
Interpretazione dei grafici di regressione
Fino a questo punto, Abbiamo appreso importanti ipotesi di regressione e metodi da intraprendere, se tali presupposti vengono violati.
Ma non è la fine. Ora, dovresti conoscere le soluzioni anche per affrontare la violazione di questi presupposti. In questa sezione, ho spiegato il 4 grafici di regressione insieme a metodi per superare i limiti delle ipotesi.
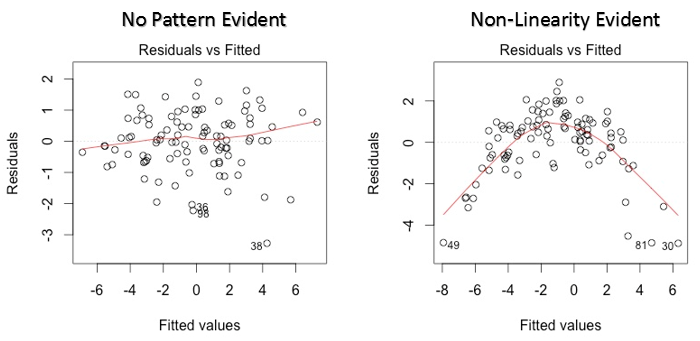
1. Valori residui vs. valori adattati
Questo grafico a dispersione mostra la distribuzione dei residui (errori) rispetto ai valori adattati (valori previsti). È una delle trame più importanti che tutti dovrebbero imparare. Rivela vari spunti utili, inclusi valori anomali. I valori anomali in questo grafico sono etichettati dal loro numero di osservazione, che li rende facili da individuare.
Ci sono due cose importanti che devi imparare:
- Se c'è qualche schema (può essere, una forma parabolica) in questo grafico, consideralo come un segno di non linearità nei dati. Significa che il modello non cattura effetti non lineari.
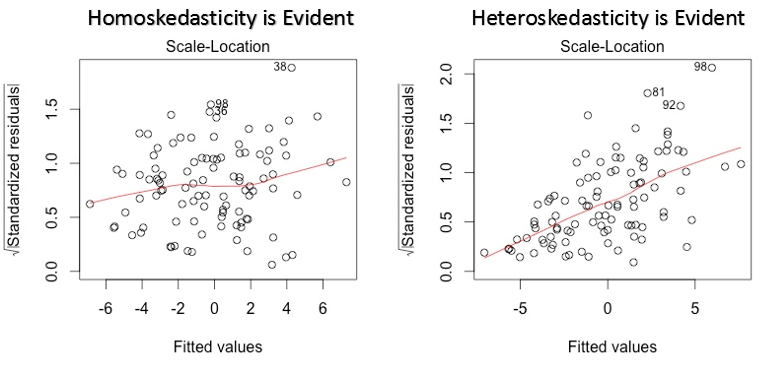
- Se la forma di un imbuto è evidente nel grafico, consideralo come un segno di varianza non costante, vale a dire, eteroschedasticità.
Soluzione: Per superare il problema della non linearità, puoi fare una trasformazione non lineare di predittori come log (X), X o X² trasformano la variabile dipendente. Per superare l'eteroschedasticità, un modo possibile è trasformare la variabile di risposta come log (E) il Y. Cosa c'è di più, puoi usare il metodo dei minimi quadrati ponderati per affrontare l'eteroschedasticità.
2. Grafico QQ normale
Questo qq o quantile-quantile è un diagramma di dispersione che ci aiuta a convalidare l'ipotesi di distribuzione normale in un insieme di dati. Usando questo grafico possiamo dedurre se i dati provengono da una distribuzione normale. Se è così, il grafico mostrerebbe una linea abbastanza retta. C'è un'assenza di normalità negli errori con deviazione in linea retta.
Se ti chiedi cos'è un 'quantile', ecco una semplice definizione: pensa ai quantili come punti nei tuoi dati al di sotto dei quali cade una certa proporzione di dati. Il quantile è spesso chiamato percentile. Ad esempio: quando diciamo che il valore percentile 50 è 120, significa che la metà dei dati è inferiore 120.
Soluzione: Se gli errori non sono distribuiti normalmente, la trasformazione non lineare delle variabili (risposta o predittori) può portare un miglioramento nel modello.
3. Grafico posizione scala
Questo grafico viene utilizzato anche per rilevare l'omoschedasticità (ipotesi di uguale varianza). Mostra come i residui sono distribuiti nell'intervallo di predittori.. È simile al grafico del valore residuo rispetto al grafico rettificato, tranne per il fatto che utilizza valori residui standardizzati. Idealmente, non ci dovrebbero essere schemi riconoscibili nella trama. Ciò implicherebbe che gli errori sono distribuiti normalmente. Ma, nel caso in cui il grafico mostri uno schema riconoscibile (probabilmente a forma di imbuto), implicherebbe una distribuzione degli errori non normale.
Soluzione: Segui la soluzione per l'eteroschedasticità fornita nel grafico 1.
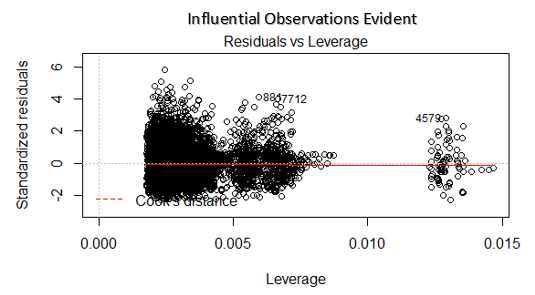
4. Grafico residuo vs leva finanziaria
Conosciuto anche come diagramma della distanza di Cook. La distanza di Cook cerca di identificare i punti che hanno più influenza di altri punti. Tali punti di influenza tendono ad avere un impatto considerevole sulla linea di regressione.. In altre parole, l'aggiunta o la rimozione di tali punti dal modello può modificare completamente le statistiche del modello.
Ma, Queste osservazioni influenti possono essere trattate come valori anomali?? Questa domanda può essere risolta solo dopo aver esaminato i dati. Perciò, in questo grafico, grandi valori contrassegnati dalla distanza di cottura possono richiedere ulteriori indagini.
Soluzione: Per influenzare le osservazioni che non sono altro che valori anomali, si non molti, puoi eliminare quelle righe. In alternativa, puoi ridurre l'osservazione degli outlier con il valore massimo nei dati o trattare quei valori come valori mancanti.
Argomento di studio: Come ho migliorato il mio modello di regressione usando la trasformazione logaritmica
Note finali
Puoi sfruttare il vero potere dell'analisi di regressione applicando le soluzioni descritte sopra.. L'implementazione di queste correzioni in R è piuttosto semplice. Se vuoi conoscere qualche soluzione specifica in R, Puoi lasciare un commento, Sarò felice di aiutarti con le risposte..
Lo scopo di questo articolo era di aiutarti a ottenere le informazioni e la prospettiva sottostanti delle ipotesi e dei diagrammi di regressione.. In questo modo, avrai più controllo sulla tua analisi e potrai modificare l'analisi in base alle tue esigenze.
Hai trovato questo articolo utile? Hai usato queste correzioni per migliorare le prestazioni del modello?? Condividi la tua esperienza / suggerimenti nei commenti.
