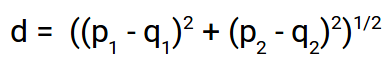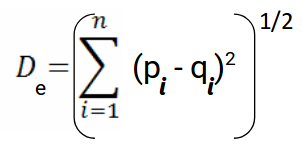Le metriche della distanza sono una parte fondamentale di vari algoritmi di apprendimento automatico. Estas métricas de distancia se utilizan tanto en el apprendimento supervisionatoL'apprendimento supervisionato è un approccio di apprendimento automatico in cui un modello viene addestrato utilizzando un set di dati etichettati. Ogni input nel set di dati è associato a un output noto, consentendo al modello di imparare a prevedere i risultati per nuovi input. Questo metodo è ampiamente utilizzato in applicazioni come la classificazione delle immagini, Riconoscimento vocale e previsione delle tendenze, sottolineandone l'importanza in... como no supervisado, generalmente per calcolare la somiglianza tra i punti dati.
Una metrica della distanza efficace migliora le prestazioni del nostro modello di apprendimento automatico, sia per l'ordinamento o il raggruppamento di attività.
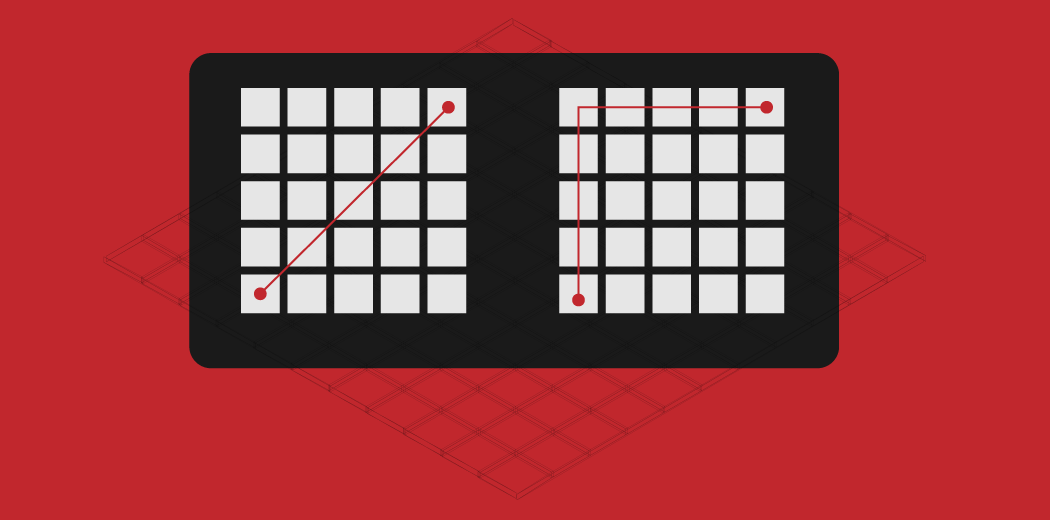
Supponiamo di voler creare cluster utilizzando l'algoritmo K-Means Clustering o Nearest Neighbor per risolvere un problema di classificazione o regressione.. Come definiresti la somiglianza tra le diverse osservazioni qui?? Come possiamo dire che due punti sono simili tra loro??
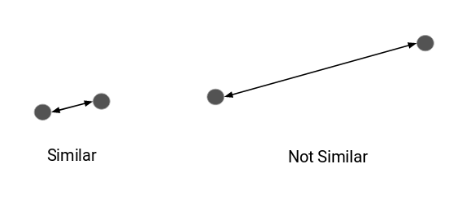
Questo accadrà se le loro caratteristiche sono simili, verità? Quando tracciamo questi punti, saranno più vicini l'uno all'altro in lontananza.
Perciò, possiamo calcolare la distanza tra i punti e quindi definire la somiglianza tra loro. Ecco la domanda da un milione di dollari: Come calcoliamo questa distanza e quali sono le diverse metriche di distanza nell'apprendimento automatico??
Questo è ciò che intendiamo rispondere in questo articolo. analizzeremo 4 tipi di metriche di distanza in apprendimento automatico e capire come funzionano in Chiodo.
4 tipi di metriche di distanza nell'apprendimento automatico
- distanza euclidea
- Distanza da Manhattan
- Minkowski distanza
- Distanza di Hamming
Iniziamo con la metrica di distanza più utilizzata: la distanza euclidea.
1. distanza euclidea
La distanza euclidea rappresenta la distanza più breve tra due punti.
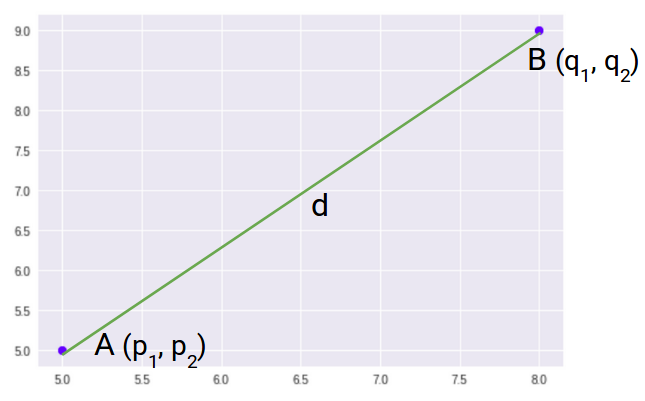
La maggior parte degli algoritmi di apprendimento automatico, compreso K-Mezzi, usa questa metrica di distanza per misurare la somiglianza tra le osservazioni. Diciamo che abbiamo due punti come mostrato di seguito:
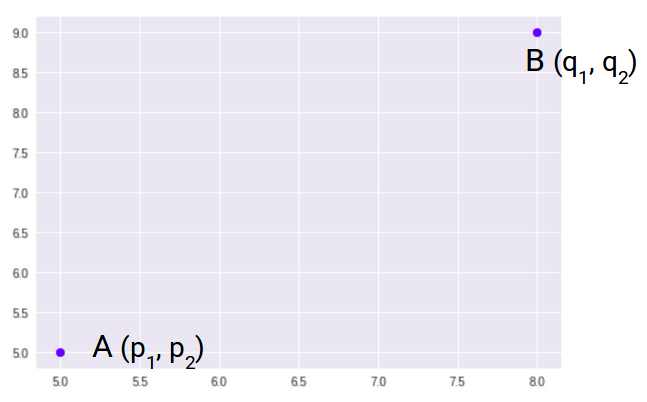
Quindi, la distanza euclidea tra questi due punti A e B sarà:
Ecco la formula per la distanza euclidea:
Usiamo questa formula quando si tratta di 2 dimensioni. Possiamo generalizzare questo per uno spazio n-dimensionale come:
In cui si,
- n = numero di dimensioni
- pi, qi = punti dati
Codifichiamo la distanza euclidea in Chiodo. Questo ti darà una migliore comprensione di come funziona questa metrica di distanza..
Per prima cosa importeremo le librerie necessarie. Userò la libreria SciPy che contiene codici prescritti per la maggior parte delle funzioni di distanza utilizzate in Python:
Questi sono i due punti campione che useremo per calcolare le diverse funzioni di distanza. Calcoliamo ora la distanza euclidea tra questi due punti:
Ecco come possiamo calcolare la distanza euclidea tra due punti in Python. Ora capiamo la metrica della seconda distanza, la distanza da Manhattan.
2. Distanza da Manhattan
La distanza di Manhattan è la somma delle differenze assolute tra i punti in tutte le dimensioni.
Possiamo rappresentare la distanza da Manhattan come:
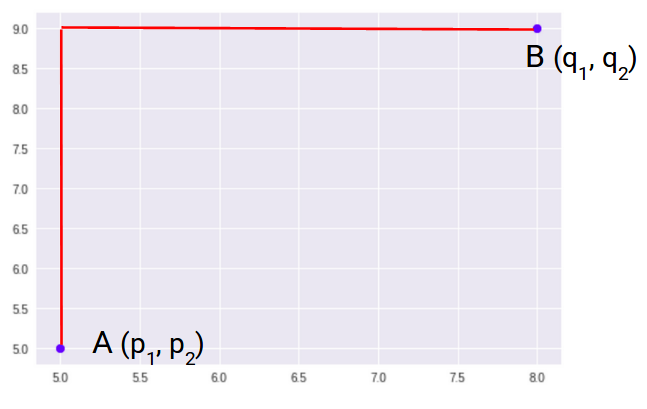
Poiché la rappresentazione di cui sopra è bidimensionale, calcolare la distanza da Manhattan, faremo la somma delle distanze assolute nelle direzioni x e y. Quindi, la distanza da Manhattan in uno spazio bidimensionale è data come:
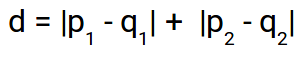
E la formula generalizzata per uno spazio n-dimensionale è data come:
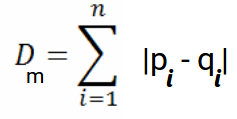
In cui si,
- n = numero di dimensioni
- pi, qi = punti dati
Ora, calcoleremo la distanza di Manhattan tra i due punti:
Notare che La distanza da Manhattan è anche conosciuta come la distanza dell'isolato. SciPy ha una funzione chiamata isolato che restituisce la distanza di Manhattan tra due punti.
Diamo ora un'occhiata alla seguente metrica di distanza: la distanza di Minkowski.
3. Minkowski distanza
La distanza di Minkowski è la forma generalizzata della distanza euclidea e di Manhattan.
La formula per la distanza di Minkowski è data come:
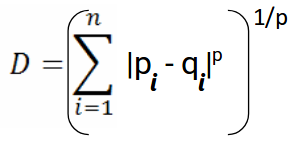
Qui, p rappresenta l'ordine della norma. Calcoliamo la distanza Minkowski dell'ordine 3:
Il parametro p della metrica della distanza SciPy Minkowski rappresenta l'ordine della norma. Quando ordine (P) è 1, rappresenterà la distanza da Manhattan e quando l'ordine nella formula sopra è 2, rappresenterà la Distanza Euclidea.
Verifichiamolo in Python:
Qui, puoi vederlo quando l'ordine è 1, sia Minkowski che Manhattan Distance sono uguali. Controlliamo anche la distanza euclidea:
Quando l'ordine è 2, possiamo vedere che le distanze Minkowski ed Euclidea sono le stesse.
Fino ad ora, abbiamo coperto le metriche di distanza utilizzate quando si tratta di variabili continue o numeriche. Ma E se avessimo variabili categoriali?? Come possiamo decidere la somiglianza tra le variabili categoriali?? Qui è dove possiamo usare un'altra metrica di distanza chiamata Hamming Distance.
4. Distanza di Hamming
La distanza di Hamming misura la somiglianza tra due corde della stessa lunghezza. La distanza di Hamming tra due stringhe della stessa lunghezza è il numero di posizioni in cui i caratteri corrispondenti sono diversi.
Comprendiamo il concetto con un esempio. Diciamo che abbiamo due stringhe:
“Euclidiana” e “Manhattan”
Poiché la lunghezza di queste stringhe è uguale, possiamo calcolare la distanza di Hamming. Andremo personaggio per personaggio e uniremo le catene. Il primo carattere di entrambe le stringhe (e e m rispettivamente) è diverso. Allo stesso modo, il secondo carattere di entrambe le stringhe (uya) è diverso. e così via.
Guarda attentamente: sette caratteri sono diversi, mentre due personaggi (gli ultimi due caratteri) sono simili:
Perciò, la distanza di Hamming qui sarà 7. Nota che maggiore è la distanza di Hamming tra due corde, più diverse saranno queste stringhe (e viceversa).
Vediamo come possiamo calcolare la distanza di Hamming di due stringhe in Python. Primo, definiremo due stringhe che useremo:
Queste sono le due corde “euclideo” e “Manhattan” che abbiamo visto anche nell'esempio. Calcoliamo ora la distanza di Hamming tra queste due stringhe:
Come abbiamo visto nell'esempio precedente, la distanza di Hamming tra "euclidea" e "manhattan" è 7. Abbiamo anche visto che la distanza di Hamming funziona solo quando abbiamo corde della stessa lunghezza.
Vediamo cosa succede quando abbiamo catene di lunghezze diverse:
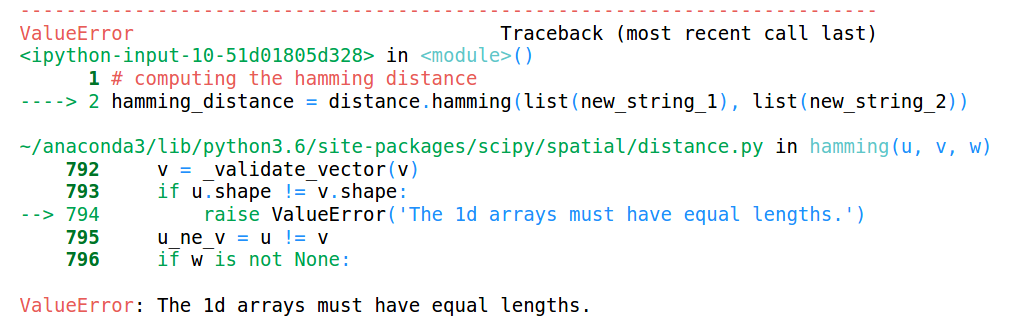
Puoi vedere che le lunghezze di entrambe le catene sono diverse. Vediamo cosa accadrà quando proveremo a calcolare la distanza di Hamming tra queste due stringhe:
Questo genera un errore che dice che le lunghezze degli array devono essere le stesse. Perché, La distanza di Hamming funziona solo quando abbiamo stringhe o array della stessa lunghezza.
Queste sono alcune delle misure di somiglianza o matrici di distanza che vengono generalmente utilizzate nel Machine Learning.
