Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
Sommario
Cos'è la regressione lineare??
Importanza della regressione lineare nell'analisi predittiva.
Applicazione pratica della regressione lineare usando R.
Applicazione per set di dati di pressione sanguigna ed età.
Che cos'è una regressione lineare?
L'analisi di regressione lineare semplice è una tecnica per trovare l'associazione tra due variabili. Las dos variables involucradas son una variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... dependiente que responde al cambio y la variable independiente. Nota che non stiamo calcolando la dipendenza della variabile dipendente dalla variabile indipendente, solo l'associazione.
Ad esempio, un'azienda sta investendo una certa quantità di denaro nella commercializzazione di un prodotto e ha anche raccolto dati di vendita nel corso degli anni analizzando la correlazione tra budget di marketing e dati di vendita, possiamo prevedere la vendita del prossimo anno se l'azienda stanzia una certa somma di denaro per il reparto marketing. L'idea di previsione di cui sopra sembra magica, ma è pura statistica. La regressione lineare consiste fondamentalmente nell'adattare una linea retta al nostro set di dati in modo da poter prevedere eventi futuri.
La linea più adatta sarebbe della forma:
Y = B0 + B1X
In cui si, E – Variabile dipendente
X – Variabile indipendente
B0 e B1 – Parametro di regressione
Previsione della pressione sanguigna per età mediante regressione in R
Equazione della retta di regressione nel nostro set di dati.
PA = 98,7147 + 0,9709 Età
Importazione del set di dati
Importa un set di dati età vs pressione sanguigna che è un file CSV utilizzando la funzione read.csv () in R e memorizza questo set di dati in un dataframe bp.
bp <- leggi.csv ("bp.csv")
Crea frame di dati per prevedere i valori
Creazione di un data frame che memorizzerà l'età di 53 anni. E questo frame di dati verrà utilizzato per prevedere la pressione sanguigna a 53 anni dopo la creazione di un modello di regressione lineare.
P <- as.data.frame(53) colnames(P) <- "Età"
Creando un Diagramma di dispersioneIl grafico a dispersione è uno strumento grafico utilizzato in statistica per visualizzare la relazione tra due variabili. Consiste in un insieme di punti in un piano cartesiano, dove ogni punto rappresenta una coppia di valori corrispondenti alle variabili analizzate. Questo tipo di grafico consente di identificare i modelli, Tendenze e possibili correlazioni, facilitare l'interpretazione dei dati e il processo decisionale sulla base delle informazioni visive presentate.... usando la biblioteca ggplot2
Prendendo l'aiuto della libreria ggplot2 in R, possiamo vedere che esiste una correlazione tra pressione sanguigna ed età, come possiamo vedere che l'aumento dell'età è seguito da un aumento della pressione sanguigna.
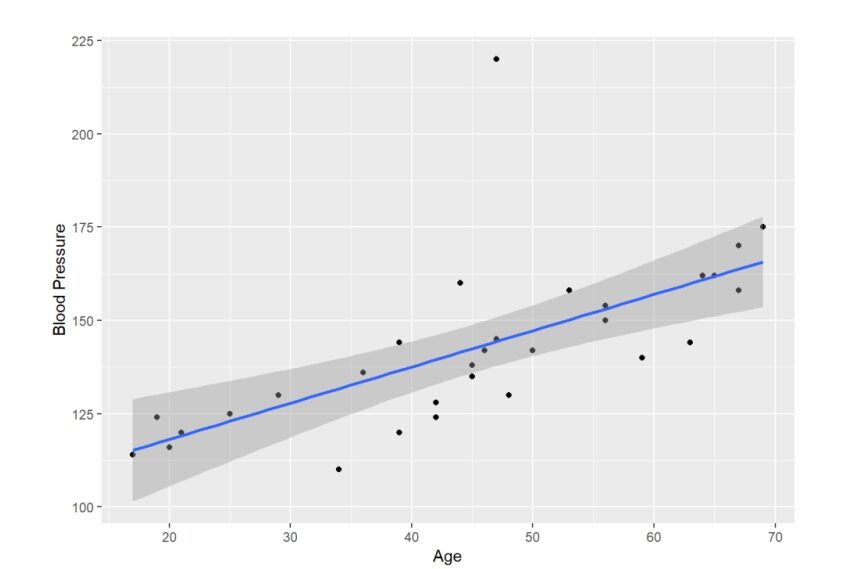
È abbastanza evidente dal grafico che la distribuzione sul grafico è sparsa in modo tale da poter adattare una retta passante per i punti.
Calcola la correlazione tra età e pressione sanguigna
Possiamo anche verificare la nostra precedente analisi che esiste una correlazione tra pressione sanguigna ed età prendendo l'aiuto della funzione cor () in R che viene utilizzato per calcolare la correlazione tra due variabili.
cor(bp$BP,bp$Età)
[1] 0,6575673
Creare un modello di regressione lineare
Ora, con l'aiuto della funzione lm (), facciamo un modello lineare. La funzione lm () ha due attributi, prima è una formula in cui useremo “BP ~ Età” perché l'età è una variabile indipendente e la pressione sanguigna è una variabile dipendente e la seconda sono i dati, dove daremo il nome del frame di dati che contiene i dati che in questo caso è il frame di dati bp.
modello <- lm(BP ~ Età, dati = bp)
Riepilogo del nostro modello di regressione lineare
riepilogo(modello)
Produzione:
## ## Chiamata: ## lm(formula = PA ~ Età, dati = bp) ## ## Residui: ## Min 1Q Mediana 3Q Max ## -21.724 -6.994 -0.520 2.931 75.654 ## ## Coefficienti: ## Stima Standard. Valore di errore t Pr(>|T|) ## (Intercettare) 98.7147 10.0005 9.871 1.28e-10 *** ## Età 0.9709 0.2102 4.618 7.87e-05 *** ## --- ## Significato. codici: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Errore standard residuo: 17.31 Su 28 gradi di libertà ## R-quadrato multiplo: 0.4324, R-quadrato rettificato: 0.4121 ## Statistica F: 21.33 Su 1 e 28 DF, valore p: 7.867e-05
Interpretazione del modello
## Coefficienti: ## Stima Standard. Valore di errore t Pr(>|T|) ## (Intercettare) 98.7147 10.0005 9.871 1.28e-10 *** ## Età 0.9709 0.2102 4.618 7.87e-05 *** ## --- ## Significato. codici: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 B0 = 98.7147 (E- intercettare) B1 = 0.9709 (Coefficiente di età) PA = 98.7147 + 0.9709 Età
Significa che un cambiamento in un'unità di età porterà 0.9709 unità per modificare la pressione sanguigna.
Errore standard È la variabilità attesa nel coefficiente che cattura la variabilità campionaria, quindi la variazione nell'intersezione può essere fino a 10.0005 e la variazione di età sarà 0.2102 niente di più
Valore T: il valore t è il coefficiente diviso per l'errore standard, è fondamentalmente quanto grande è stimato in relazione all'errore, maggiore è il coefficiente rispetto a Std. errore più alto è il t-score e il t-score viene fornito con un p-value perché la sua distribuzione Il p-value è quanto statisticamente significativa è la variabile per il modello per un livello di confidenza del 95% confronteremo questo valore con alfa che sarà 0.05 , quindi nel nostro caso il p-value dell'intersezione e l'Età è minore di alfa (alfa = 0.05), ciò implica che entrambi sono statisticamente significativi per il nostro modello.
## Errore standard residuo: 17.31 Su 28 gradi di libertà
## R quadrato multiplo: 0,4324, R quadrato montato: 0,4121
## Statistica F: 21,33 Su 1 e 28 DF, valore p: 7,867e-05
Errore standard residuo o l'errore standard del modello è fondamentalmente l'errore medio per il modello che è 17.31 nel nostro caso e significa che il nostro modello può avere un errore medio di 17.31 mentre predice la pressione sanguigna. Più piccolo è l'errore, migliore sarà il modello durante la previsione.
R-quadrato multiplo è la ragione per (1- (somma dell'errore al quadrato / somma dei quadrati totali))
R quadrato montato:
Se aggiungiamo variabili, non importa se è significativo nella previsione o meno, il valore di R al quadrato aumenterà, motivo per cui viene utilizzato R al quadrato corretto perché se la variabile aggregata non è significativa per la previsione del modello, il valore R aggiustato -squared si ridurrà, è uno degli strumenti più utili per evitare il sovradattamento del modello.
F – statistiche è il rapporto tra il quadrato medio del modello e il quadrato medio dell'errore, in altre parole, è il motivo per cui il modello funziona bene e cosa sta causando l'errore, e maggiore è il valore F, meglio funziona il modello rispetto all'errore.
Uno sono i gradi di libertà del numeratore della statistica F e 28 è il grado di libertà degli errori.
Prevedere il valore della pressione sanguigna a 53 anni
PA = 98,7147 + 0,9709 Età
La formula di cui sopra verrà utilizzata per calcolare la pressione sanguigna all'età di 53 anni e questo sarà raggiunto utilizzando la funzione di previsione () prima scriveremo il nome del modello di regressione lineare separandolo da una virgola dando il valore del nuovo set di dati in p dall'età 53 è stato precedentemente salvato nel frame di dati p.
prevedere(modello, nuovi dati = p)
## 1
## 150.1708
Quindi, il valore previsto della pressione sanguigna è 150,17 al 53 anni.
Come abbiamo previsto la pressione sanguigna con l'associazione dell'età, ora potrebbe essere coinvolta più di una variabile indipendente che mostra una correlazione con una variabile dipendente chiamata regressione multipla.
Modello di regressione lineare multipla
L'analisi di regressione multilineare è una tecnica statistica per trovare l'associazione di più variabili indipendenti nella variabile dipendente.. Ad esempio, il reddito generato da un'azienda dipende da diversi fattori, compresa la dimensione del mercato, il prezzo, la promozione, il prezzo della concorrenza, eccetera. Fondamentalmente, il modello di regressione lineare multipla stabilisce una relazione lineare tra una variabile dipendente e più variabili indipendenti.
L'equazione di regressione lineare multipla è la seguente:
Y = B0 + B1X1 + B2X2 + .. + BnXk + E
In cui si
E – Variabile dipendente
X – Variabile indipendente
B0, B1, B3,. – Coefficienti di regressione lineare multipla
E- Errore
Prendendo un altro esempio dal dataset di Wine e con l'aiuto di AGST, HarvestRain prevediamo il prezzo del vino.
Importazione del set di dati
Utilizzo della funzione read.csv (), importare il set di dati wine.csv e wine_test.csv rispettivamente nel data frame wine e wine_test.
vino <- leggi.csv("vino.csv")
wine_test <- leggi.csv("wine_test.csv")Scarica il set di dati dal basso
Trova la correlazione tra diverse variabili
Uso della funzione cor () e la funzione rotonda () possiamo arrotondare la correlazione tra tutte le variabili nel dataset del vino a due cifre decimali.
il giro(cor(vino),2)
Produzione:
Anno Prezzo InvernoRain AGST HarvestRain Age FranciaPop ## Anno 1.00 -0.45 0.02 -0.25 0.03 -1.00 0.99 ## Prezzo -0.45 1.00 0.14 0.66 -0.56 0.45 -0.47 ## InvernoPioggia 0.02 0.14 1.00 -0.32 -0.28 -0.02 0.00 ## AGST -0.25 0.66 -0.32 1.00 -0.06 0.25 -0.26 ## VendemmiaPioggia 0.03 -0.56 -0.28 -0.06 1.00 -0.03 0.04 ## Età -1.00 0.45 -0.02 0.25 -0.03 1.00 -0.99 ## FranciaPop 0.99 -0.47 0.00 -0.26 0.04 -0.99 1.00
Trame sparse
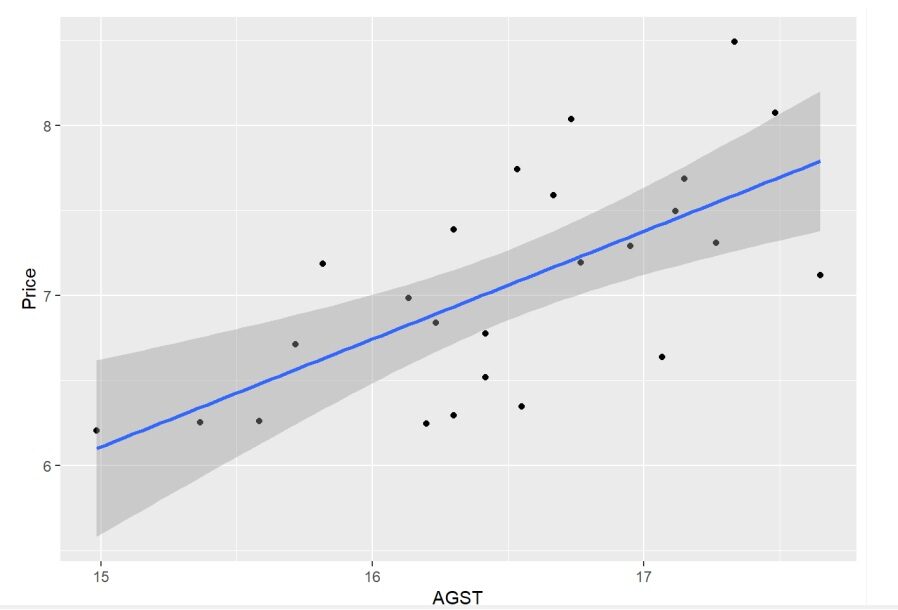
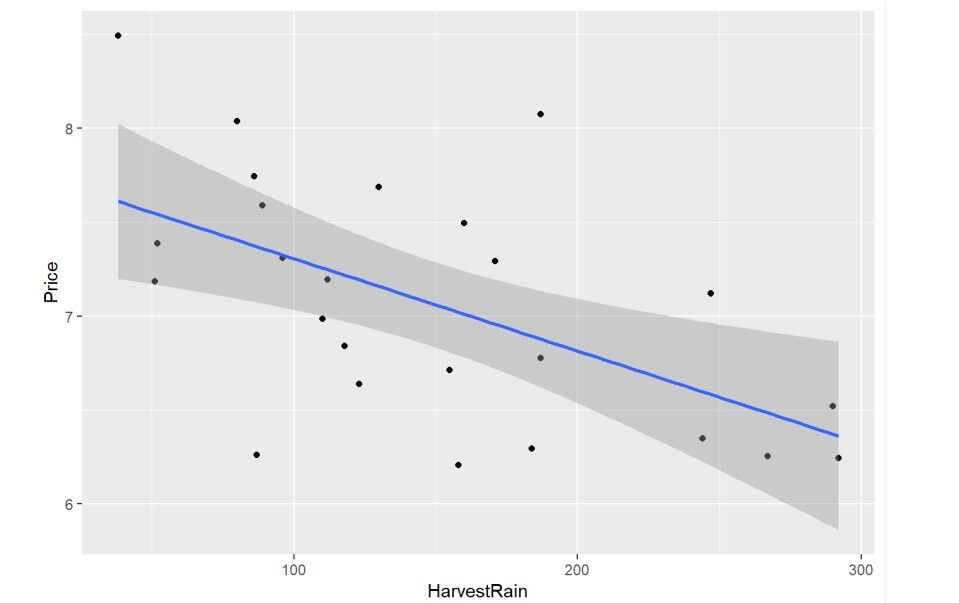
Quando si utilizza la libreria ggplot2 in R, creare un grafico a dispersione che possa mostrare chiaramente che AGST e il prezzo del vino sono altamente correlati. Nello stesso modo, il grafico a dispersioneUn gráfico de dispersión es una representación visual que muestra la relación entre dos variables numéricas mediante puntos en un plano cartesiano. Cada eje representa una variable, y la ubicación de cada punto indica su valor en relación con ambas. Este tipo de gráfico es útil para identificar patrones, correlaciones y tendencias en los datos, facilitando el análisis y la interpretación de relaciones cuantitativas.... entre HarvestRain y el precio del vino también muestra su correlación.
ggplot(vino,aes(x = AGST, y = Prezzo)) + geom_point() +geom_smooth(metodo = "lm")
ggplot(vino,aes(x = HarvestRain, y = Prezzo)) + geom_point() +geom_smooth(metodo = "lm")
Creare un modello di regressione multilineare
modello1 <- lm(Prezzo ~ AGST + VendemmiaPioggia,dati = vino) riepilogo(modello1)
Produzione:
## ## Chiamata: ## lm(formula = Prezzo ~ AGST + VendemmiaPioggia, dati = vino) ## ## Residui: ## Min 1Q Mediana 3Q Max ## -0.88321 -0.19600 0.06178 0.15379 0.59722 ## ## Coefficienti: ## Stima Standard. Valore di errore t Pr(>|T|) ## (Intercettare) -2.20265 1.85443 -1.188 0.247585 ## AGST 0.60262 0.11128 5.415 1.94e-05 *** ## VendemmiaPioggia -0.00457 0.00101 -4.525 0.000167 *** ## --- ## Significato. codici: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Errore standard residuo: 0.3674 Su 22 gradi di libertà ## R-quadrato multiplo: 0.7074, R-quadrato rettificato: 0.6808 ## Statistica F: 26.59 Su 2 e 22 DF, valore p: 1.347e-06
Interpretazione del modello
## Coefficienti: ## Stima Standard. Valore di errore t Pr(>|T|) ## (Intercettare) -2.20265 1.85443 -1.188 0.247585 ## AGST 0.60262 0.11128 5.415 1.94e-05 *** ## VendemmiaPioggia -0.00457 0.00101 -4.525 0.000167 *** ## Significato. codici: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 B0 = 98.7147 (E- intercettare) B1 = 0.9709 (Coefficiente di età) Prezzo = -2.20265 + 0.60262 AGST - 0.00457 VendemmiaPioggia
Significa che un cambiamento in un'unità in AGST porterà 0,60262 unità per cambiare di prezzo e un cambiamento di unità in HarvestRain porterà 0,00457 unità da cambiare di prezzo.
Errore standard è la variabilità attesa nel coefficiente che cattura la variabilità campionaria, quindi la variazione nell'intersezione può essere fino a 1.85443 e la variazione in AGST sarà 0.11128 e la variazione in HarvestRain è 0.00101 niente di più
Valore T: il valore t è il coefficiente diviso per l'errore standard, è fondamentalmente quanto grande è stimato in relazione all'errore, maggiore è il coefficiente rispetto a Std. errore maggiore è il t-score e il t-score viene fornito con un p-value perché è una distribuzione. Il p-value è quanto statisticamente significativa è la variabile per il modello per un livello di confidenza del 95% confronteremo questo valore con alfa per essere 0.05, quindi nel nostro caso il p-value dell'intersezione, AGST e HarvestRain è inferiore a alfa (alfa = 0.05), questo implica che sono tutti statisticamente significativi per il nostro modello.
## Errore standard residuo: 0.3674 Su 22 gradi di libertà
## R quadrato multiplo: 0,7074, R quadrato montato: 0,6808
## Statistica F: 26.59 Su 2 e 22 DF, valore p: 1.347e-06
Errore standard residuo o l'errore standard del modello è fondamentalmente l'errore medio per il modello che è 0.3674 nel nostro caso e significa che il nostro modello può avere una differenza media di 0.3674 pur prevedendo il prezzo dei vini. Più piccolo è l'errore, migliore sarà il modello durante la previsione.
R-quadrato multiplo è la ragione per (1- (somma dell'errore al quadrato / somma dei quadrati totali))
R quadrato montato:
Se aggiungiamo variabili, non importa se è significativo nella previsione o meno, il valore di R al quadrato aumenterà, motivo per cui viene utilizzato R al quadrato corretto perché se la variabile aggregata non è significativa per la previsione del modello, il valore R aggiustato -squared si ridurrà, è uno degli strumenti più utili per evitare il sovradattamento del modello.
F – statistiche è il rapporto tra il quadrato medio del modello e il quadrato medio dell'errore, in altre parole, è il motivo per cui il modello funziona bene e cosa sta causando l'errore, e maggiore è il valore F, meglio funziona il modello rispetto all'errore.
Due sono i gradi di libertà del numeratore della statistica F e 22 è il grado di libertà degli errori.
Predire i valori per la nostra suite di test
predizione <- prevedere(modello1, newdata = wine_test)
Valori previsti con il set di dati di prova
degustazione di vini
## Anno Prezzo InvernoRain AGST HarvestRain Age FranciaPop ## 1 1979 6.9541 717 16.1667 122 4 54835.83 ## 2 1980 6.4979 578 16.0000 74 3 55110.24
predizione
## 1 2 ## 6.982126 7.101033
conclusione
Come possiamo vedere dal set di dati disponibili possiamo creare un modello di regressione lineare e addestrare quel modello, se sono disponibili dati sufficienti, possiamo prevedere con precisione nuovi eventi o, in altre parole, risultati futuri.
