Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.
introduzione
Interessato all'analisi predittiva? Dopo, ricerca sull'intelligenza artificiale, el aprendizaje automático y el apprendimento profondoApprendimento profondo, Una sottodisciplina dell'intelligenza artificiale, si affida a reti neurali artificiali per analizzare ed elaborare grandi volumi di dati. Questa tecnica consente alle macchine di apprendere modelli ed eseguire compiti complessi, come il riconoscimento vocale e la visione artificiale. La sua capacità di migliorare continuamente man mano che vengono forniti più dati lo rende uno strumento chiave in vari settori, dalla salute.... .
Se sei sulla strada dell'apprendimento della scienza dei dati, capire sicuramente cos'è l'apprendimento automatico. Nel mondo digitale di oggi, tutti sanno cos'è l'apprendimento automatico perché era una tecnologia digitale di moda in tutto il mondo.
Ogni passo verso l'adattamento al mondo futuro è guidato da questa tecnologia attuale, e questa tecnologia attuale è guidata da scienziati dei dati come te e me😌.
Qui si parla solo di machine learning, se non sai cos'è, vi diamo una breve introduzione:
Apprendimento automatico è lo studio degli algoritmi informatici, che migliorano automaticamente attraverso l'esperienza e attraverso l'uso dei dati. il tuo algoritmo costruisce un modello basato sui dati che forniamo durante la creazione del modello. Questa è la semplice definizione di machine learning, e quando andiamo in profondità, abbiamo scoperto che ci sono molti algoritmi che vengono utilizzati nella costruzione di modelli. In genere, gli algoritmi di machine learning più utilizzati si basano sul tipo di problema, i ragazzi sono fondamentalmente regressione, classificazione, ecc... Ma qui parleremo solo di algoritmi di regressione.
Facciamo una breve introduzione su cos'è la regressione. Regressione è il metodo statistico degli investimenti, finanza e altre discipline che tentano di determinare la forza e la relazione tra variabili indipendenti e dipendenti. In genere, le variabili indipendenti sono quelle variabili in cui i loro valori vengono utilizzati per ottenere l'output e le variabili dipendenti sono quelle il cui valore dipende da valori indipendenti. Quando si parla di algoritmi di regressione, alcuni algoritmi di regressione comunemente usati vengono utilizzati per addestrare il modello di apprendimento automatico, come semplice regressione lineare, nastro, cresta, eccetera.
Perciò, Parliamo di regressione lineare multipla e capiamo in dettaglio come la regressione lineare semplice differisce dalla regressione lineare multipla.
- Regressione lineare semplice vs regressione lineare multipla
- Set di dati
- Leggi set di dati
- Variabili indipendenti e dipendenti
- Gestione delle variabili categoriali
- Divisione dati
- Applicazione del modello
Regressione lineare semplice contro regressione lineare multipla
Ora, prima di andare avanti, analizziamo l'interazione dietro la semplice regressione lineare, quindi proviamo a confrontare la regressione lineare semplice e multipla basata su quell'intuizione che stiamo effettivamente facendo con il nostro problema di apprendimento automatico.
Regressione lineare semplice
Consideriamo una semplice regressione lineare in qualsiasi algoritmo di apprendimento automatico usando l'esempio,
Ora, Supponiamo di prendere uno scenario di prezzo della casa in cui il nostro asse x è la dimensione della casa e l'asse y è fondamentalmente il prezzo della casa. In questo fondamentalmente, abbiamo due caratteristiche, il primo è f1 e il secondo è f2, dove,
f1 si riferisce alle dimensioni della casa e,
f2 si riferisce al prezzo della casa
quindi sì f1 diventa la funzione autonoma e f2 diventa la caratteristica dipendente, generalmente sappiamo che ogni volta che la dimensione della casa aumenta, aumenta anche il prezzo, supponiamo di disegnare punti di dispersione a caso, attraverso questo punto di dispersione cerchiamo fondamentalmente di trovare la linea di miglior adattamento e questa linea di miglior adattamento è data dall'equazione :
equazione: y = A + Bx
supponiamo, e essere il prezzo della casa e X essere la dimensione della casa, quindi questa equazione assomiglia a questa:
equazione: prezzo = A + B (dimensione)
dove,
A è un'intercetta e B è una pendenza in quell'intercetta
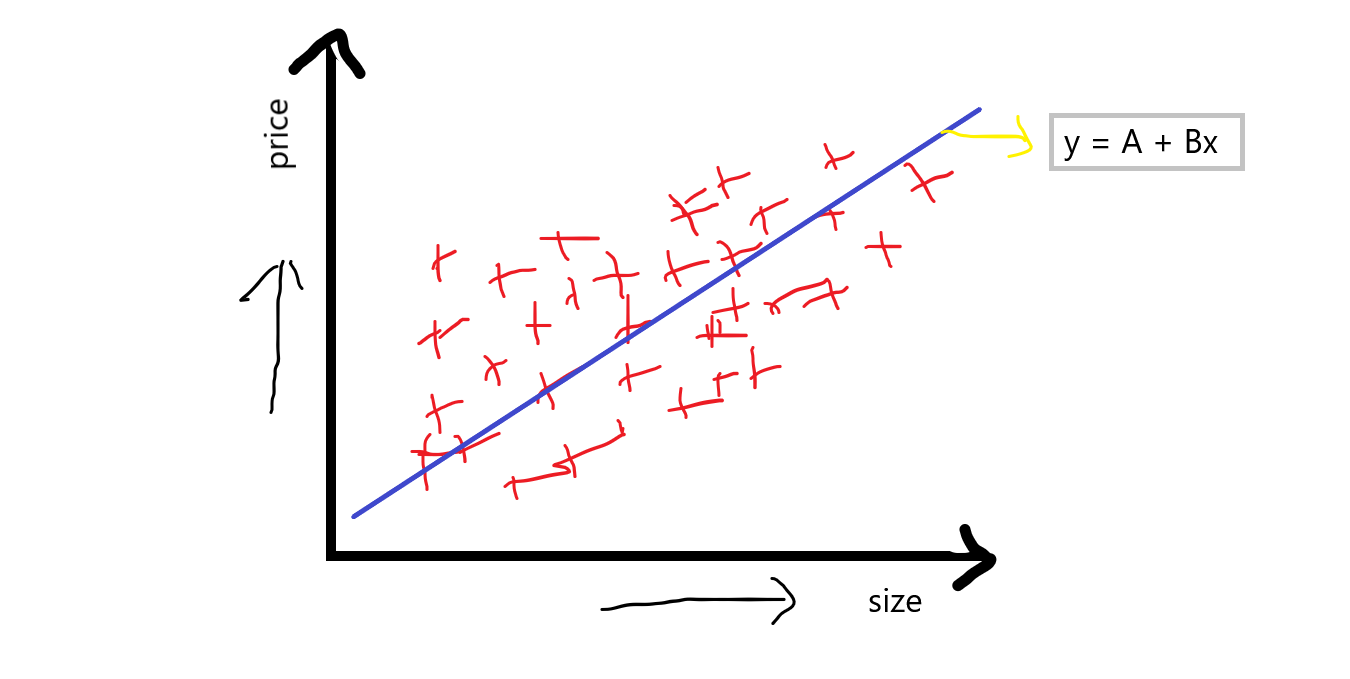
Quando discutiamo di questa equazione, in cui l'intersezione indica sostanzialmente quando il prezzo della casa è 0 allora quale sarà il prezzo base della casa, e la pendenza o coefficiente indica che con l'unità aumenta di dimensione, allora quale sarà l'unità aumenta in pendenza.
però, In cosa differisce rispetto alla regressione lineare multipla??
Regressione lineare multipla
La regressione lineare multipla indica sostanzialmente che avremo molte caratteristiche come f1, f2, f3, f4, e la nostra funzione di output f5. Se prendiamo lo stesso esempio che abbiamo discusso in precedenza, supponiamo:
f1 è la dimensione della casa.
f2 Sono brutte stanze della casa.
f3 è la città della casa.
f4 è lo stato della casa e,
f5 è la nostra caratteristica di uscita che è il prezzo della casa.
Ora, puoi vedere che più funzionalità standalone hanno un enorme impatto anche sul prezzo della casa, il prezzo può variare da caratteristica a caratteristica. Quando si parla di regressione lineare multipla, quindi la semplice equazione di regressione lineare y = A + Bx si trasforma in qualcosa come:
equazione: y = A + B1X1+ B2X2+ B3X3+ B4X4
“Se abbiamo una funzione dipendente e più funzioni indipendenti, in pratica lo chiamiamo regressione lineare multipla. “
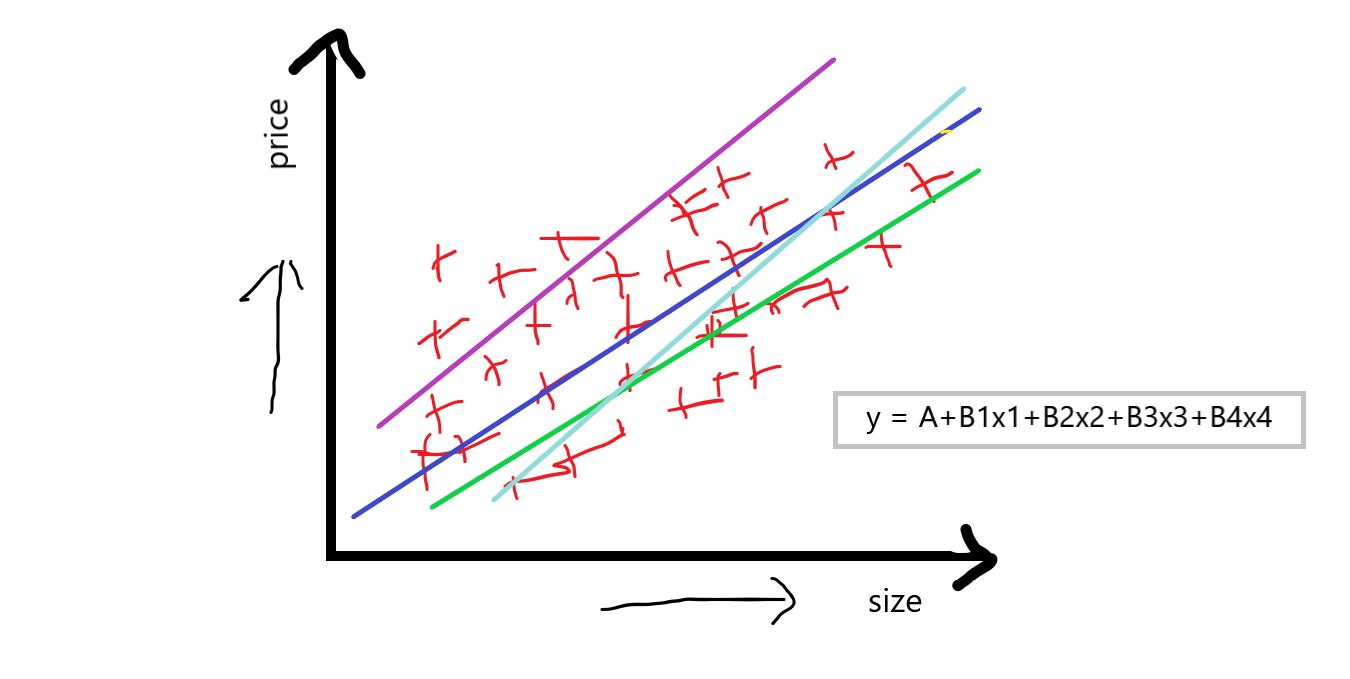
Ora, il nostro obiettivo nell'uso della regressione lineare multipla è che dobbiamo calcolare UN cos'è un incrocio?, e B1 B2 B3 B4 quali sono le pendenze o coefficienti riferiti a questa caratteristica indipendente, che sostanzialmente indica che se aumentiamo il valore di X1 di 1 guida allora B1 dice quanto valore influenzerà il prezzo della casa, e questo era simile rispetto ad altri B2 B3 B4
Quindi, questa è una breve descrizione teorica della regressione lineare multipla. Ora useremo la libreria di regressione lineare scikit impara per risolvere il problema della regressione lineare multipla.
Set di dati
Ora, applichiamo la regressione lineare multipla sul 50_startup set di dati, puoi cliccare qui per scaricare il set di dati.
Leggi set di dati
La maggior parte del set di dati è in un file CSV, per leggere questo file usiamo la libreria pandas:
df = pd.read_csv('50_Avvio.csv')
df
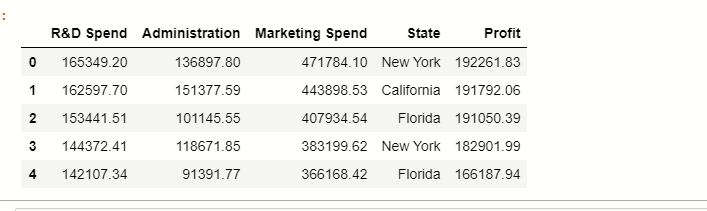
Qui puoi vedere cosa c'è 5 colonne nel set di dati in cui il stato memorizza i punti dati categorici e il resto sono caratteristiche numeriche.
Ora, dobbiamo classificare le caratteristiche indipendenti e dipendenti:
Variabili indipendenti e dipendenti
C'è un totale di 5 caratteristiche nel set di dati, in cui fondamentalmente i profitti sono la nostra caratteristica dipendente, e il resto sono le nostre caratteristiche indipendenti:
#separare gli altri attributi dall'attributo di previsione
x = df.drop('Profitto',asse=1)
#separte the predicting attribute into Y for model training
y = ['profitto']Gestione delle variabili categoriali
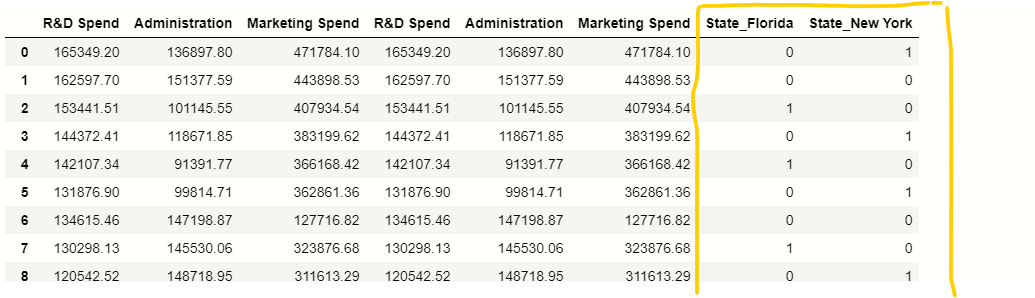
Nel nostro set di dati, c'è una colonna categorica Stato, dobbiamo gestire questi valori categorici presenti all'interno di questa colonna per cui useremo i panda get_dummy () funzione:
# maneggiare variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... categórica
stati = pd.get_dummies (X, drop_first = Vero)
# rimozione della colonna extra
x = x.drop ('Stato', asse = 1)
# concatenazione di variabili indipendenti e nuova variabile categoriale.
x = pd.concat ([X,stati], asse = 1)
X
Divisione dati
Ora, tenemos que dividir los datos en partes de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina.... y prueba para las que usamos scikit-learn train_test_split () funzione.
# importazione train_test_split da sklearn da sklearn.model_selection import train_test_split # dividere i dati x_treno, x_test, y_train, y_test = train_test_split(X, e, test_size = 0.2, stato_casuale = 42)
Applicazione del modello
Ora, applichiamo il modello di regressione lineare ai nostri dati di addestramento, primo, dobbiamo importare la regressione lineare dalla libreria scikit-learn, non esiste un'altra libreria per implementare la regressione lineare multipla, lo facciamo solo con regressione lineare.
# modulo di importazione da sklearn.linear_model import LinearRegression # creazione di un oggetto della classe LinearRegression LR = regressione lineare() # adattamento dei dati di allenamento LR.fit(x_treno,y_train)
Finalmente, se eseguiamo questo, allora il nostro modello sarà pronto, ora abbiamo i dati da x_test, Usiamo questi dati per la previsione di profitto.
y_prediction = LR.predict(x_test) y_prediction
Ora, dobbiamo confrontare i valori di y_prediction con i valori originali perché dobbiamo calcolare la precisione del nostro modello, che è stato implementato da un concetto chiamato r2_score. discutiamo brevemente di r2_score:
r2_score: –
È una funzione all'interno di sklearn. modulo metriche, dove il valore di r2_score varia tra 0 e 100 per cento, possiamo dire che è strettamente correlato a MSE.
r2 è fondamentalmente calcolato dalla formula fornita di seguito:
formula: r2 = 1 – (SSres / SSsignificare )
Ora, quando dico SSres vale a dire, è la somma dei residui e SSsignificare si riferisce alla somma dei mezzi.
dove,
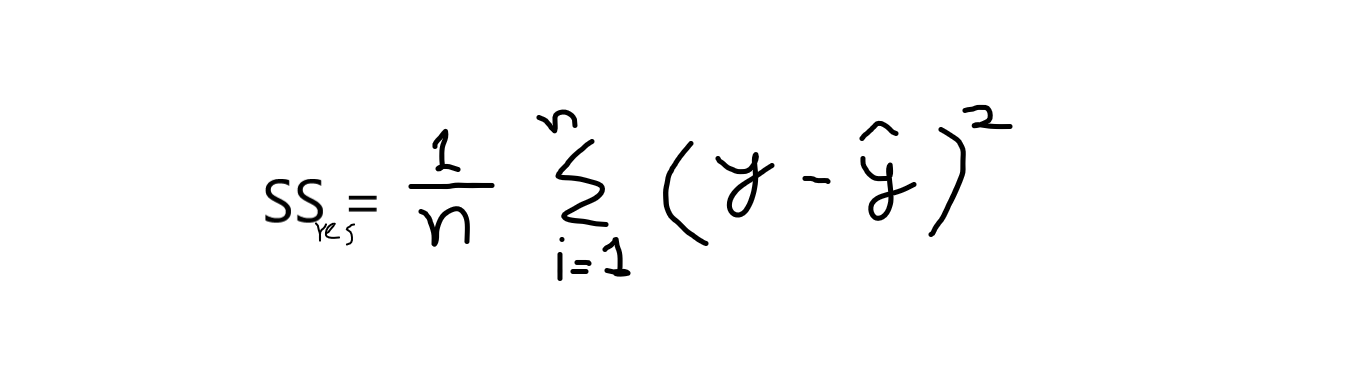
e = valori originali
e ^ = valori previsti. e,
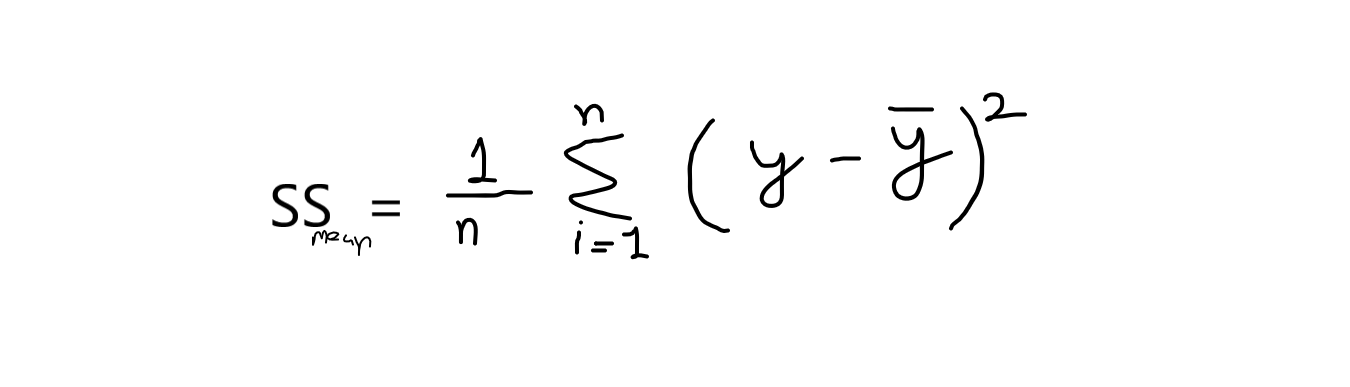
Se prendiamo il calcolo di questa equazione, allora dobbiamo sapere che il valore della somma delle medie è sempre maggiore della somma dei residui. Se questa condizione è soddisfatta, quindi il nostro modello è buono per le previsioni. I suoi valori vanno da 0,0 e 1.
“La proporzione della varianza nella variabile dipendente che è prevedibile da (S) variabile (S) Indipendente”.
Il miglior punteggio possibile è 1.0 e può essere negativo perché il modello può essere arbitrariamente peggiore. Un modello costante che predice sempre il valore atteso di y, indipendentemente dalle caratteristiche di ingresso, otterrebbe un punteggio R2 di 0.0.
# importazione del modulo r2_score
de sklearn.metrics importa r2_score
de sklearn.metrics importare mean_squared_error
# prevedere il punteggio di precisione
punteggio = r2_score (y_test, y_prediction)
Stampa ('r2 socre è', punteggiatura)
Stampa ('mean_sqrd_error è ==', mean_squared_error (y_test, y_prediction))
Stampa ('root_mean_squared errore di è ==', np.sqrt (mean_squared_error (y_test, y_prediction)))
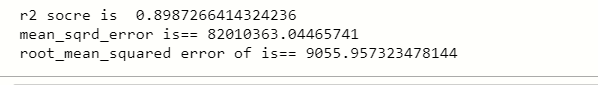
Puoi vedere che il punteggio di precisione è superiore a 0,8, il che significa che possiamo usare questo modello per risolvere più regressioni lineari, e anche il tasso di errore quadratico medio è basso.
Note finali
Ciao, scienziati dei dati 😎 sopra abbiamo fatto una discussione dettagliata sulla regressione lineare multipla, e l'esempio che usiamo è l'esempio di regressione lineare multipla perfetta. Spero che ora tu capisca meglio la regressione lineare multipla.
spero ti sia piaciuto!
Mi puoi connettere su LinkedIn: www.linkedin.com/in/mayur-badole-189221199
Cosa c'è di più, leggi gli altri miei articoli: https://www.analyticsvidhya.com/blog/author/mayurbadole2407/
Grazie.
