Grandi dati

Regressione lineare per principianti con implementazione Python

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.

Avvertimento: questo articolo è per principianti assoluti, Immagino che tu sia appena entrato nel campo dell'apprendimento automatico con alcune abilità matematiche del liceo e un po' di programmazione di base, ma non è nemmeno obbligatorio.

introduzione

La regressione lineare è l'algoritmo di apprendimento automatico supervisionato più elementare. Monitorare nel senso che l'algoritmo può rispondere alla tua domanda in base ai dati taggati che fornisci all'algoritmo. La risposta sarebbe come prevedere i prezzi delle case, classificare i cani rispetto ai gatti. Qui parleremo di un'attività di regressione utilizzando la regressione lineare. Alla fine, prevediamo i prezzi delle case in base all'area della casa.

Non voglio annoiarti tirando fuori tutte le parole del gergo del machine learning, All'inizio, quindi lasciami iniziare con l'equazione lineare più elementare. (y = mx + B) che tutti conosciamo dai tempi della scuola.

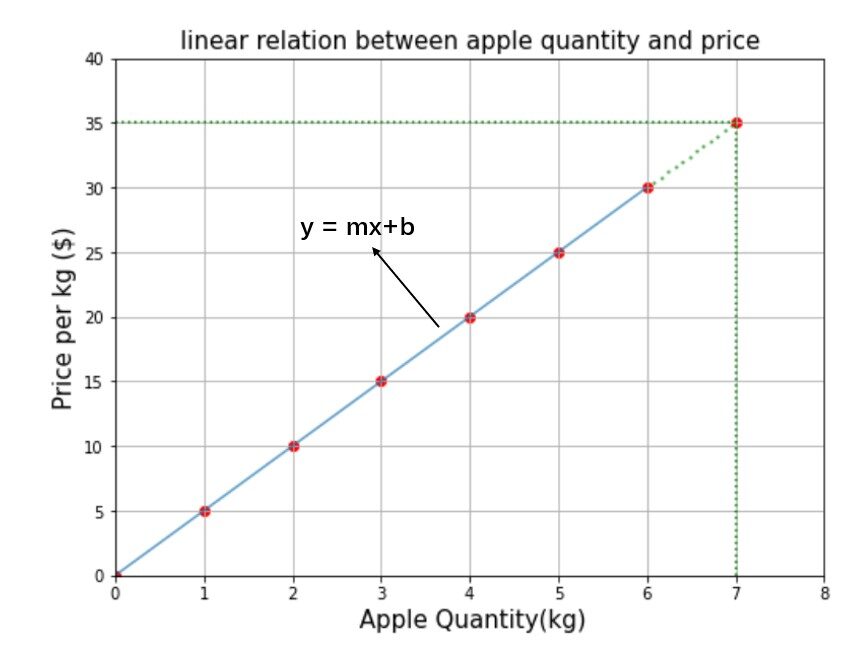
Il figura"Figura" è un termine che viene utilizzato in vari contesti, Dall'arte all'anatomia. In campo artistico, si riferisce alla rappresentazione di forme umane o animali in sculture e dipinti. In anatomia, designa la forma e la struttura del corpo. Cosa c'è di più, in matematica, "figura" è legato alle forme geometriche. La sua versatilità lo rende un concetto fondamentale in molteplici discipline.... anterior muestra la relación entre la cantidad de manzana y el precio de costo. Quanto devi pagare 7 kg di mele? So che è facile. e 1 costi kg 5 $, poi 7 costo kg 7 * 5 = 35 $ o disegnerà semplicemente una linea perpendicolare dal punto 7 lungo l'asse y fino a toccare l'equazione lineare e il valore corrispondente sull'asse y è la risposta come mostrato. dalla linea tratteggiata verde sul grafico. Ma risolveremo usando la formula di un'equazione lineare.

Ora, se devo trovare il prezzo di 9,5 kg di mela, secondo il nostro modello mx + B = 5 * 9.5 + 0 = $ 47.5 è la risposta. In questa fase, potresti averlo capito Metro e B sono gli ingredienti principali dell'equazione lineare o in altre parole Metro e B Sono chiamati parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.....

Sfortunatamente, questo non è il problema dell'apprendimento automatico né l'equazione lineare è un algoritmo di previsione, ma fortunatamente la regressione lineare genera il risultato nello stesso modo in cui lo fa l'equazione lineare. Lo scopo principale dell'algoritmo di regressione lineare è trovare il valore di Metro e B che si adattano al modello e dopo quello Metro e b sono usati prevedere il risultato dei dati di input forniti.

Prevedere i prezzi delle case

Ora scaveremo un po' più a fondo nella soluzione del problema della regressione. Guarda i campioni di dati o anche chiamato come ejemplos de addestramentoLa formazione è un processo sistematico volto a migliorare le competenze, conoscenze o abilità fisiche. Viene applicato in vari ambiti, come lo sport, Formazione e sviluppo professionale. Un programma di allenamento efficace include la pianificazione degli obiettivi, Pratica regolare e valutazione dei progressi. L'adattamento alle esigenze individuali e la motivazione sono fattori chiave per ottenere risultati di successo e sostenibili in qualsiasi disciplina.... dato nella figura sotto.

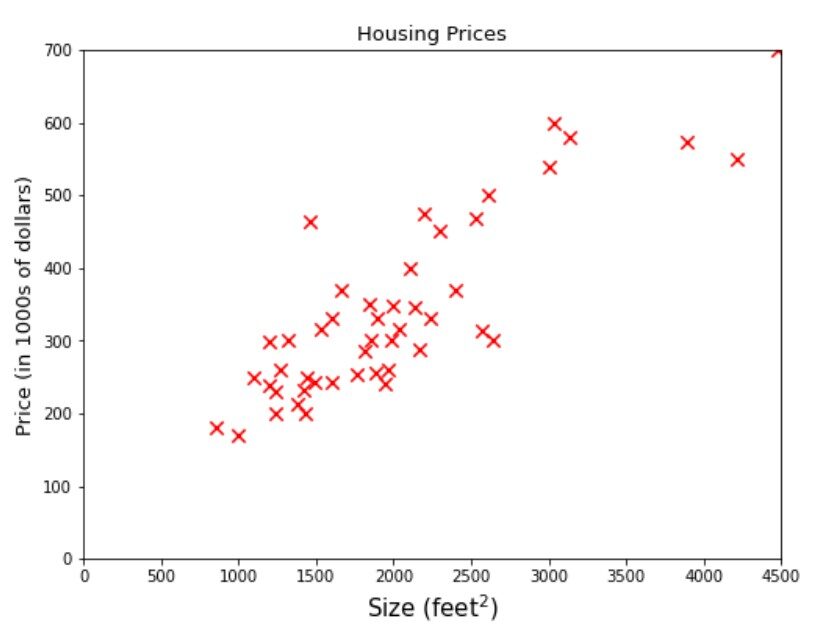
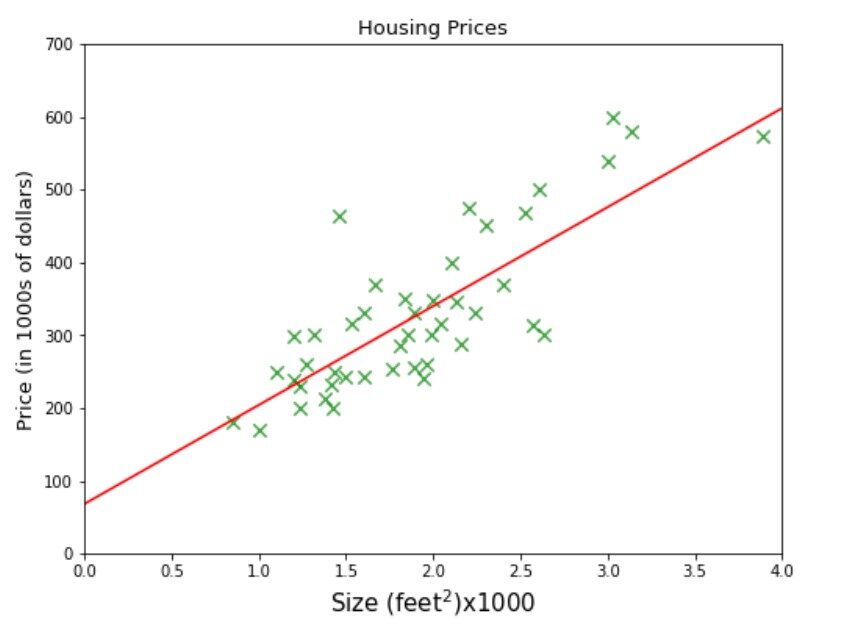
Il nome di un'azienda LA SI DO ti fornisce un dati su di lui dimensione della casa e il suo prezzo. L'azienda richiede fornendo loro un modello di apprendimento automatico che può prevedere i prezzi delle case per qualsiasi dato Taglia. Diciamo quale sarebbe il miglior prezzo stimato per un'area di 3000 piedi quadrati. Se stai pensando a avvolgere una linea da qualche parte tra il set di dati e traccia una linea verticale da 3000 sull'asse x fino a toccare la linea e poi il valore corrispondente sull'asse y, vale a dire 470 sarebbe la risposta, allora sei sulla strada giusta, è rappresentato dalla linea tratteggiata verde nella figura sottostante.

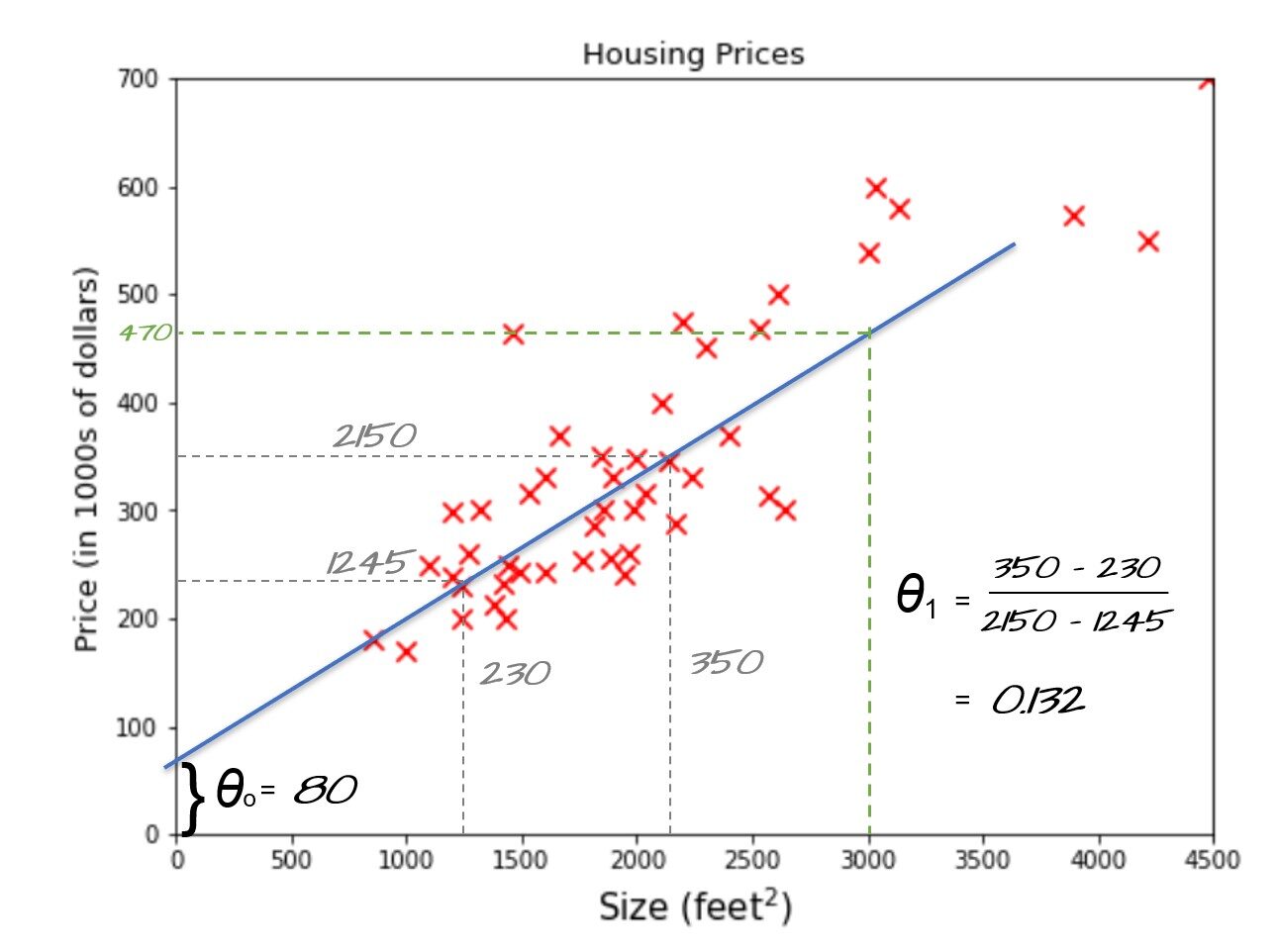
Facciamo in un altro modo, se potessimo trovare l'equazione della retta y = mx + b che usiamo per adattare i dati rappresentati dalla linea obliqua blu, quindi possiamo facilmente trovare il modello in grado di prevedere i prezzi delle case per una data area. . Basato sul gergo dell'apprendimento automatico y = mx + B Si chiama anche funzione ipotesi dove mio può essere rappresentato da rispettivamente theta0 e theta1. theta0 è anche chiamato termine di bias e theta1, theta2, .. chiamato pesos.

Vedi la linea blu nella foto sopra. Quando si prelevano due campioni che si toccano o sono molto vicini alla linea, possiamo trovare il theta1 (in sospeso) = 0.132 e zero theta = 80 come mostra l'immagine. Ora possiamo usare la nostra funzione di ipotesi per prevedere il prezzo della casa per una dimensione di 3000 piedi quadrati, vale a dire. 80 + 3000 * 0,132 = 476. $ 476,000 potrebbe essere il miglior prezzo stimato per una casa di 3000 metratura e questo potrebbe essere un modo ragionevole per preparare un modello di apprendimento automatico quando hai appena finito 50 campioni e con solo una caratteristica (dimensione).

Ma il set di dati del mondo reale potrebbe essere dell'ordine di migliaia o addirittura milioni e il numero di caratteristiche potrebbe variare tra (5–100) o anche in migliaia. A quel punto la nostra intuizione non sarà utile per trovare migliaia di parametri solo guardando un set di dati, ecco perché abbiamo bisogno di un algoritmo di apprendimento automatico per eseguire un calcolo così complesso. Avere una tazza di caffè, rinfrescati e torna indietro perché d'ora in poi capirai come funziona l'algoritmo e ti verranno presentate molte nuove terminologie. Prepararsi!!

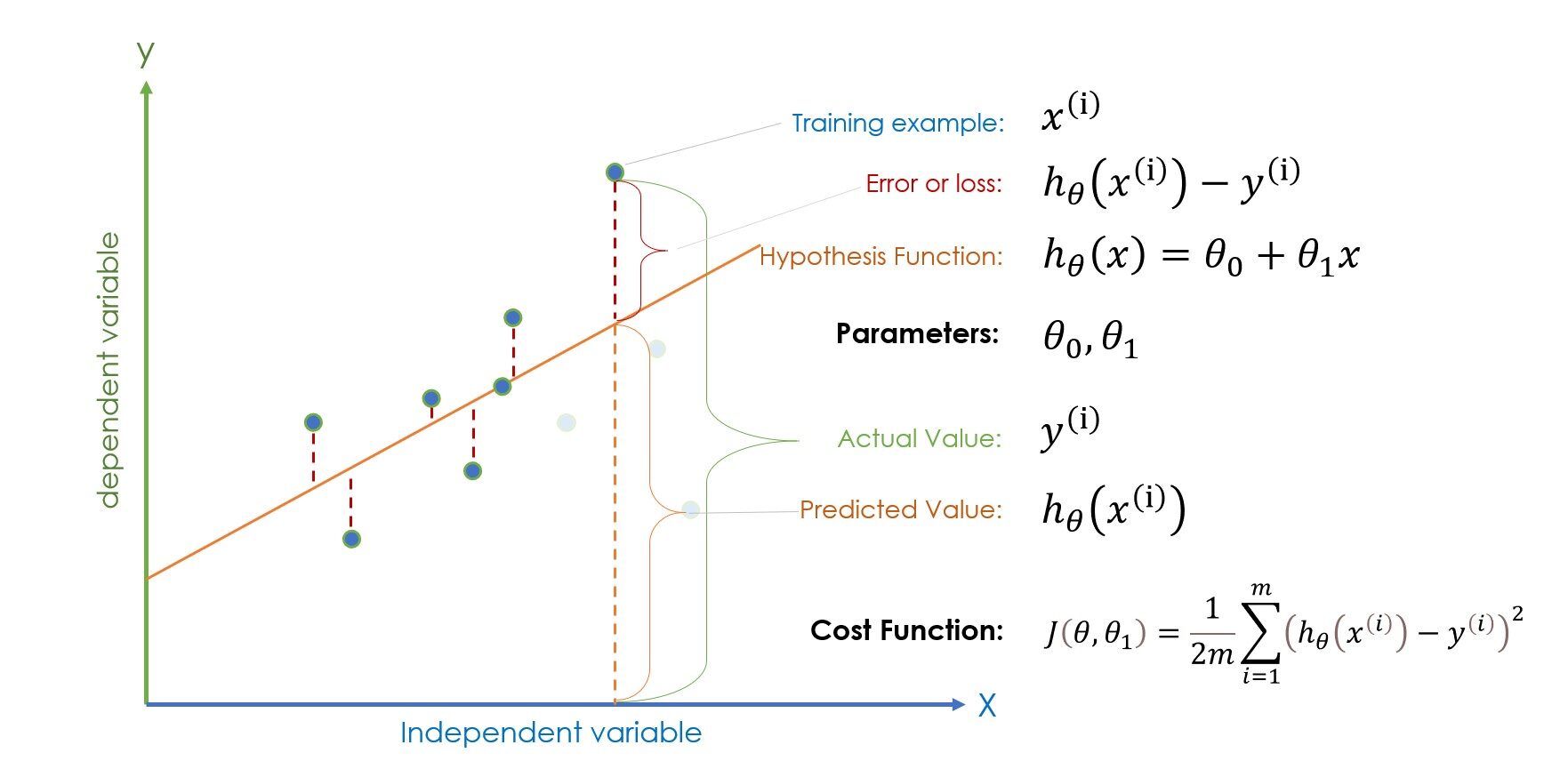
Nota: (io) nell'equazione rappresenta l'i-esimo esempio di allenamento, non il potere.

Se le terminologie fornite nella figura sopra ti sembrano extraterrestri, prenditi qualche minuto per familiarizzare e prova a trovare una connessione con ogni termine. Se lo sai fino a un certo punto, andiamo avanti. Una volta che i valori dei parametri, vale a dire termine di bias e theta1 inizializzare in modo casuale, la funzione ipotesi è pronta per la previsione, e poi il errore (|valore previsto – valore corrente|) viene calcolato per verificare se il parametro inizializzato casualmente fornisce la previsione corretta o meno.

Se l'errore è troppo alto, quindi l'algoritmo aggiorna i parametri con un nuovo valore, se l'errore è di nuovo alto, aggiornerà nuovamente i parametri con il nuovo valore. L'algoritmo continua questo processo fino a quando l'errore non viene ridotto al minimo. Per minimizzare l'errore abbiamo una funzione speciale chiamata Descenso de gradienteGradiente è un termine usato in vari campi, come la matematica e l'informatica, per descrivere una variazione continua di valori. In matematica, si riferisce al tasso di variazione di una funzione, mentre in progettazione grafica, Si applica alla transizione del colore. Questo concetto è essenziale per comprendere fenomeni come l'ottimizzazione negli algoritmi e la rappresentazione visiva dei dati, consentendo una migliore interpretazione e analisi in... ma prima, capiamo cosa Funzione di costo è e come funziona?

Qui, nella funzione di costo, stiamo cercando di trovare il quadrato di differenze tra il valore previsto e il valore effettivo di ciascun esempio di addestramento e quindi aggiungere tutti i differenze insieme o in altre parole, stiamo trovando il quadrato di errore di ciascuno esempio di addestramento e poi riassumere tutti gli errori insieme. L'output che otteniamo è semplicemente la media errore al quadrato di un particolare insieme di parametri. Ok, basta parole, facciamo il calcolo. Per semplificare il calcolo, useremo un solo parametro theta1 e un set di dati molto semplice.

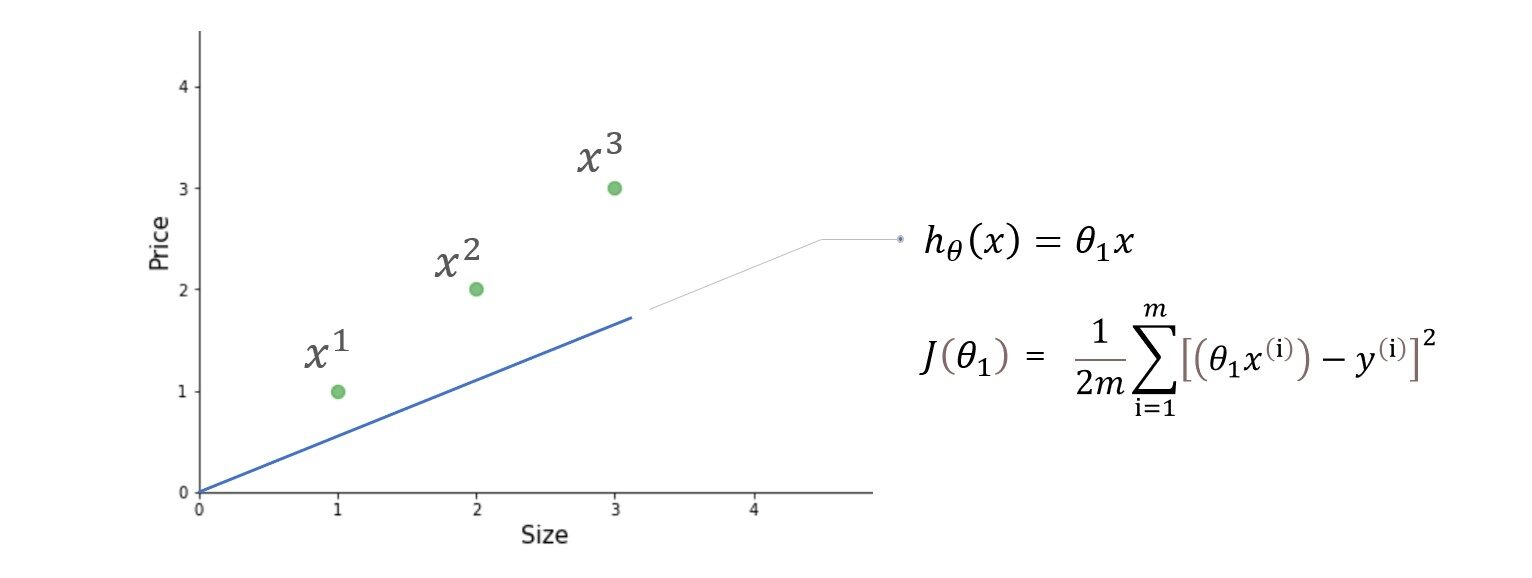
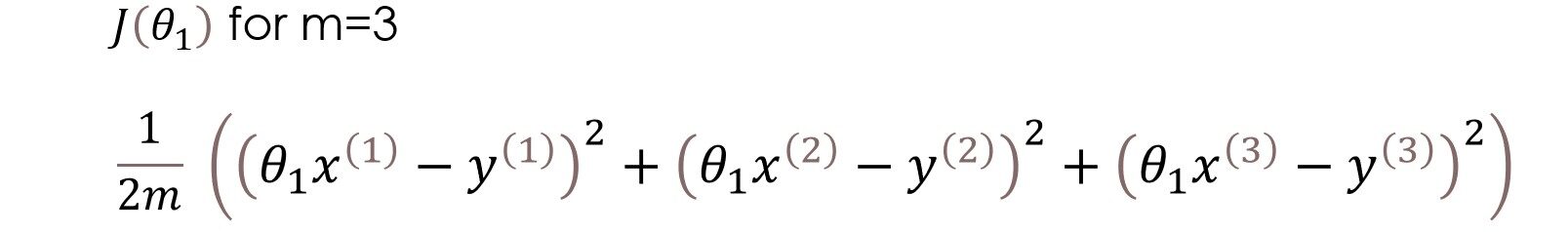
Abbiamo tre esempi di formazione (X1 = 1, y1 = 1), (X2 = 2, y2 = 2) e (X3 = 3, y3 = 3). la figura a sinistra è la funzione ipotesi e la figura a destra è la funzione di costo rappresentata graficamente per diversi valori del parametro.

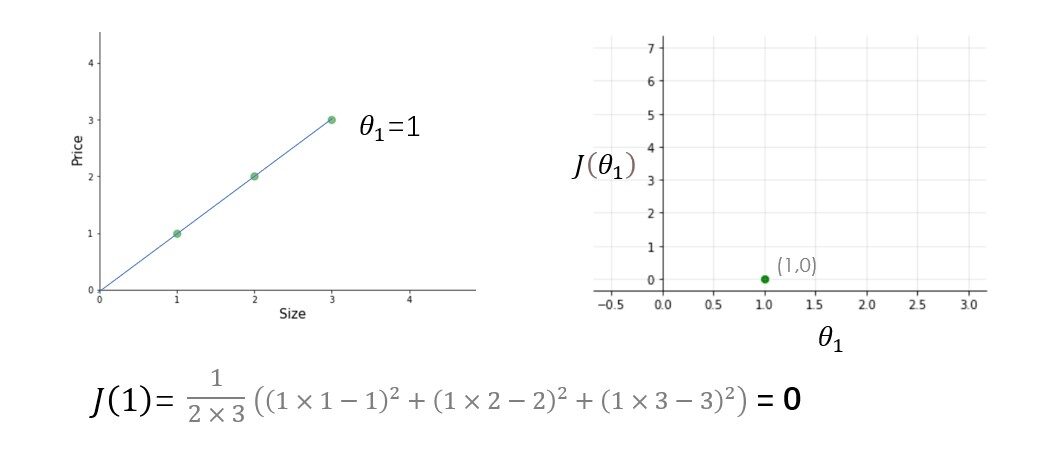
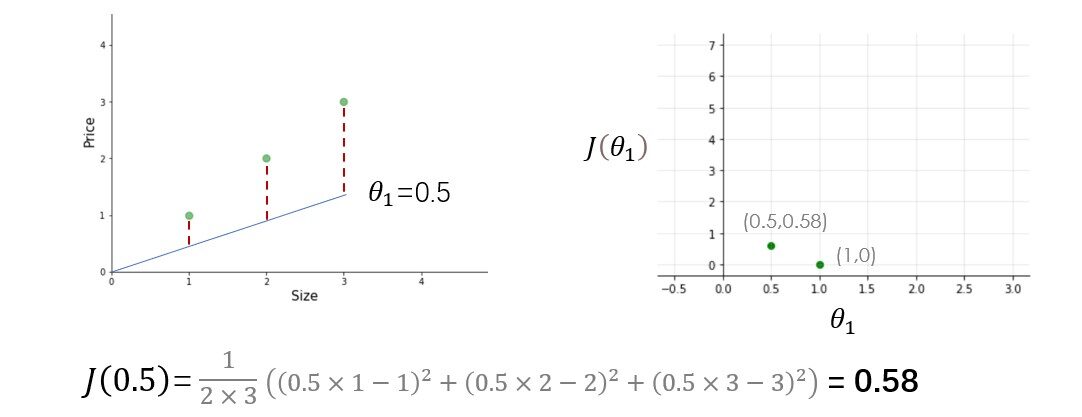
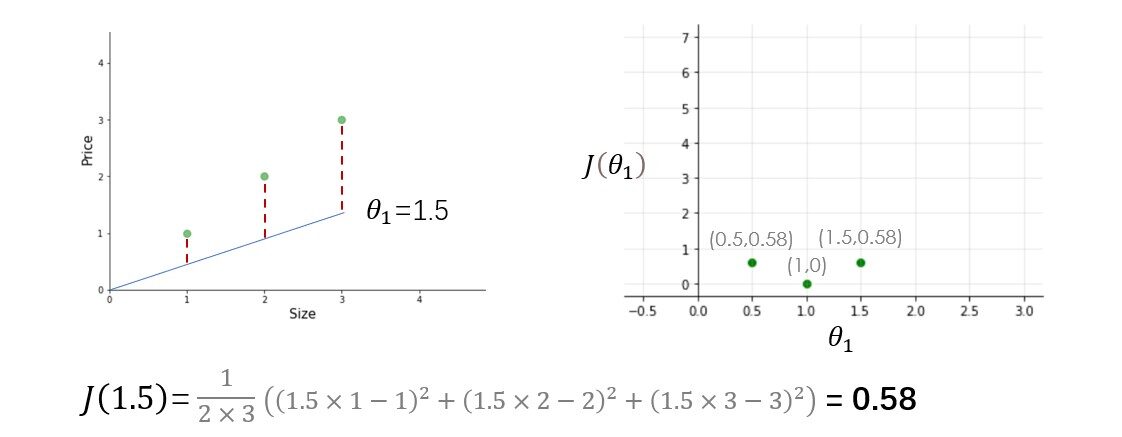
Prova tu stesso altri valori di theta1 e calcola il costo di ciascun valore di theta1. Una volta che disegno tutti questi punti, la funzione di costo apparirà come una curva a forma di ciotola come mostrato nella figura sottostante.

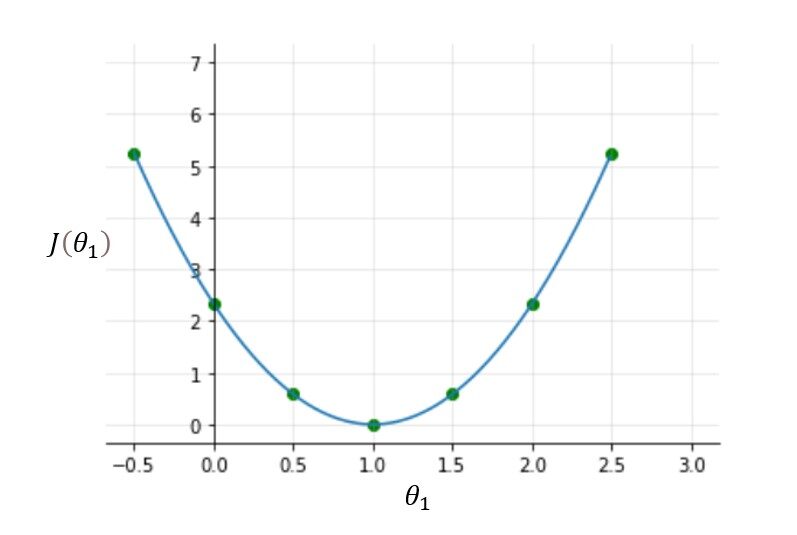
Dalla figura e dal calcolo, è chiaro che la funzione di costo è minima a theta1 = 1 o nella parte inferiore della curva a forma di ciotola. Lo scopo di tutto questo duro lavoro non è calcolare il valore minimo della funzione di costo, abbiamo un modo migliore per farlo, Invece, cerchiamo di capire il relazione Tra parametri, funzione ipotesi, e funzione di costo. Assicurati di aver compreso tutti questi concetti prima di procedere oltre..

Funzione di costo di codifica:

Discesa gradiente:

Perché abbiamo bisogno di una discesa del gradiente?

Prossimamente minimizzare la funzione di costo, Ma come? Vedremo

La funzione di costo funziona solo quando conosci i valori dei parametri.Nell'esempio di esempio sopra, scegliamo manualmente il valore dei parametri ogni volta, ma durante il calcolo algoritmico, una volta che i valori dei parametri sono stati inizializzati casualmente, è la discesa del gradiente che deve decidere quali parametri. valore da scegliere nella prossima iterazione per ridurre al minimo l'errore, è la discesa del gradiente che decide di quanto aumentare o diminuire i valori dei parametri.

Analogia: Come funziona Gradient Descent?

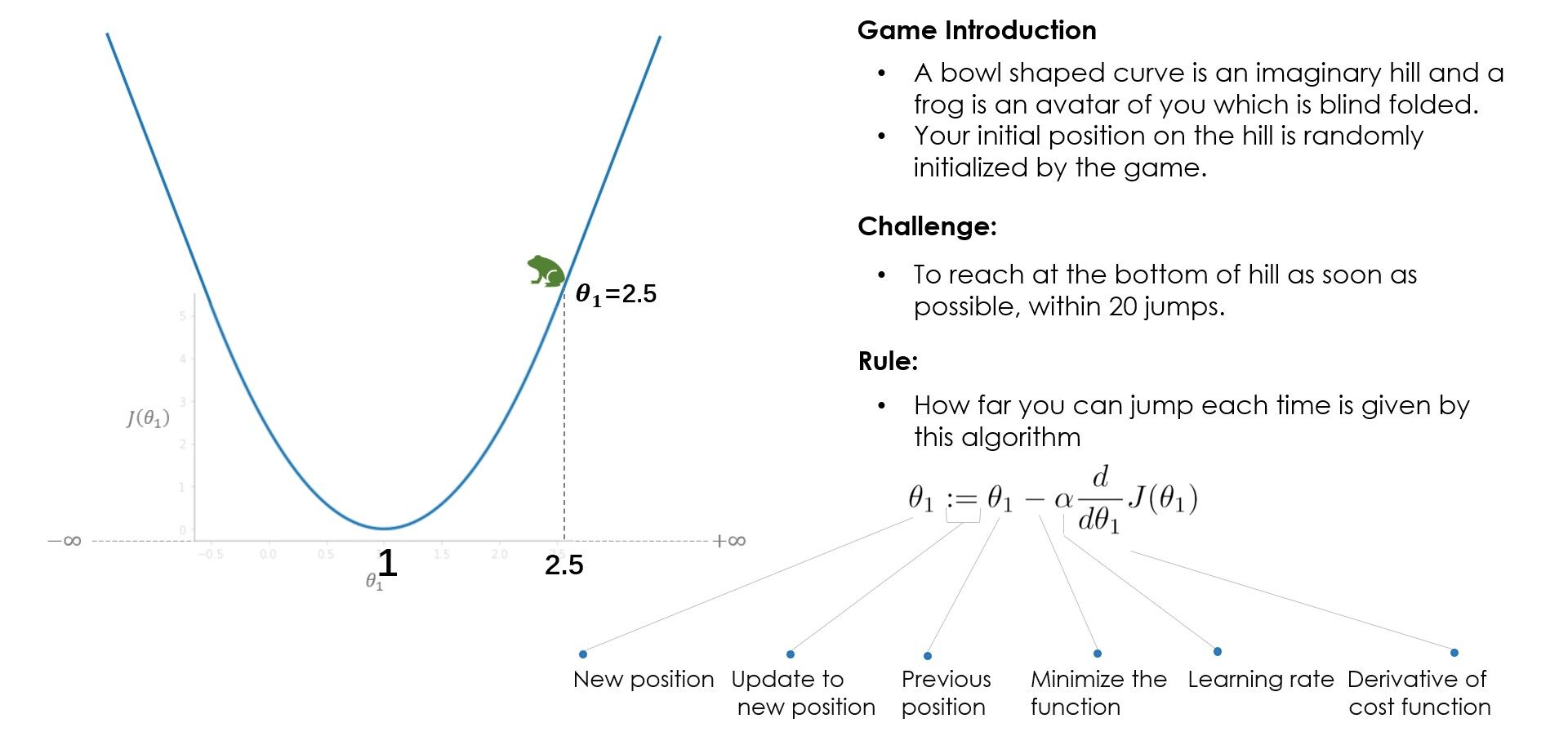
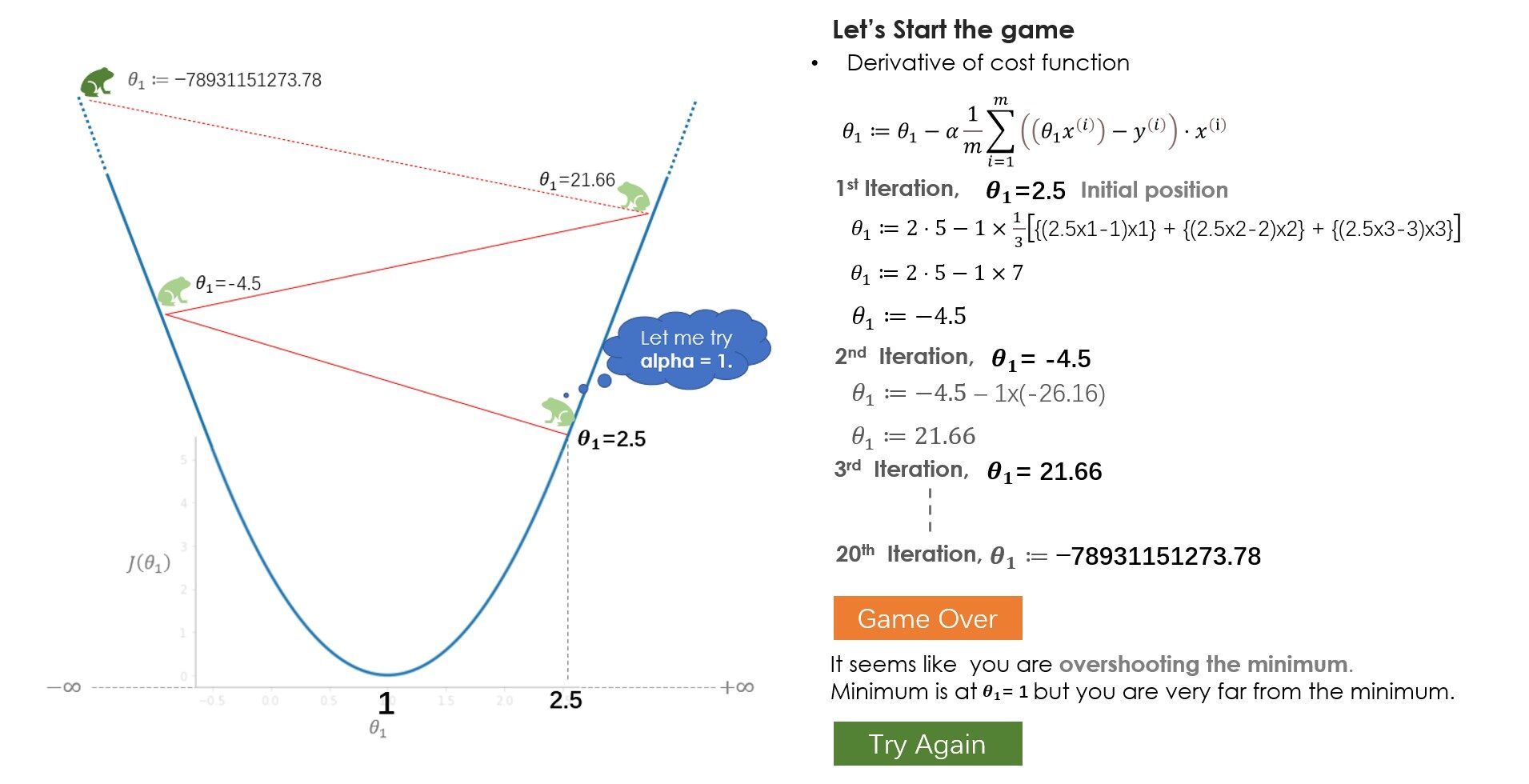
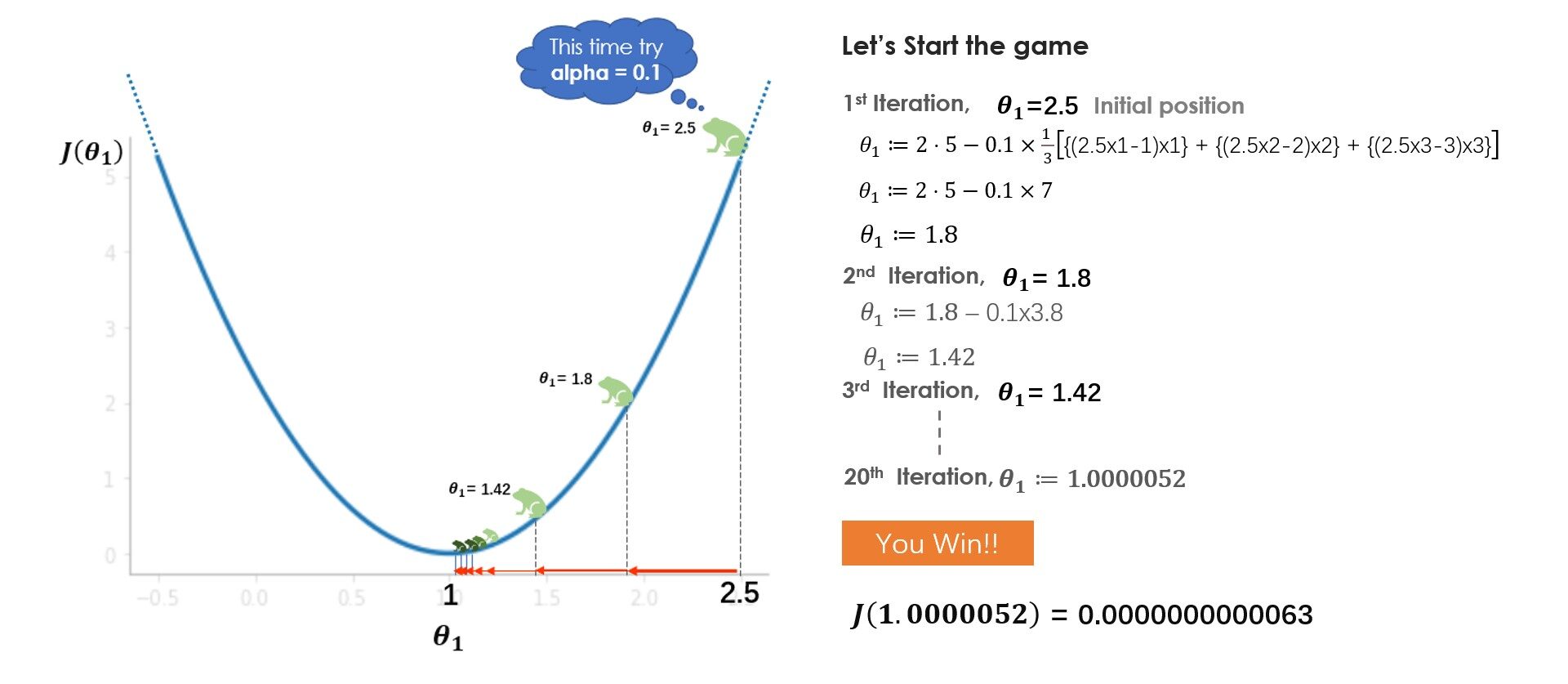
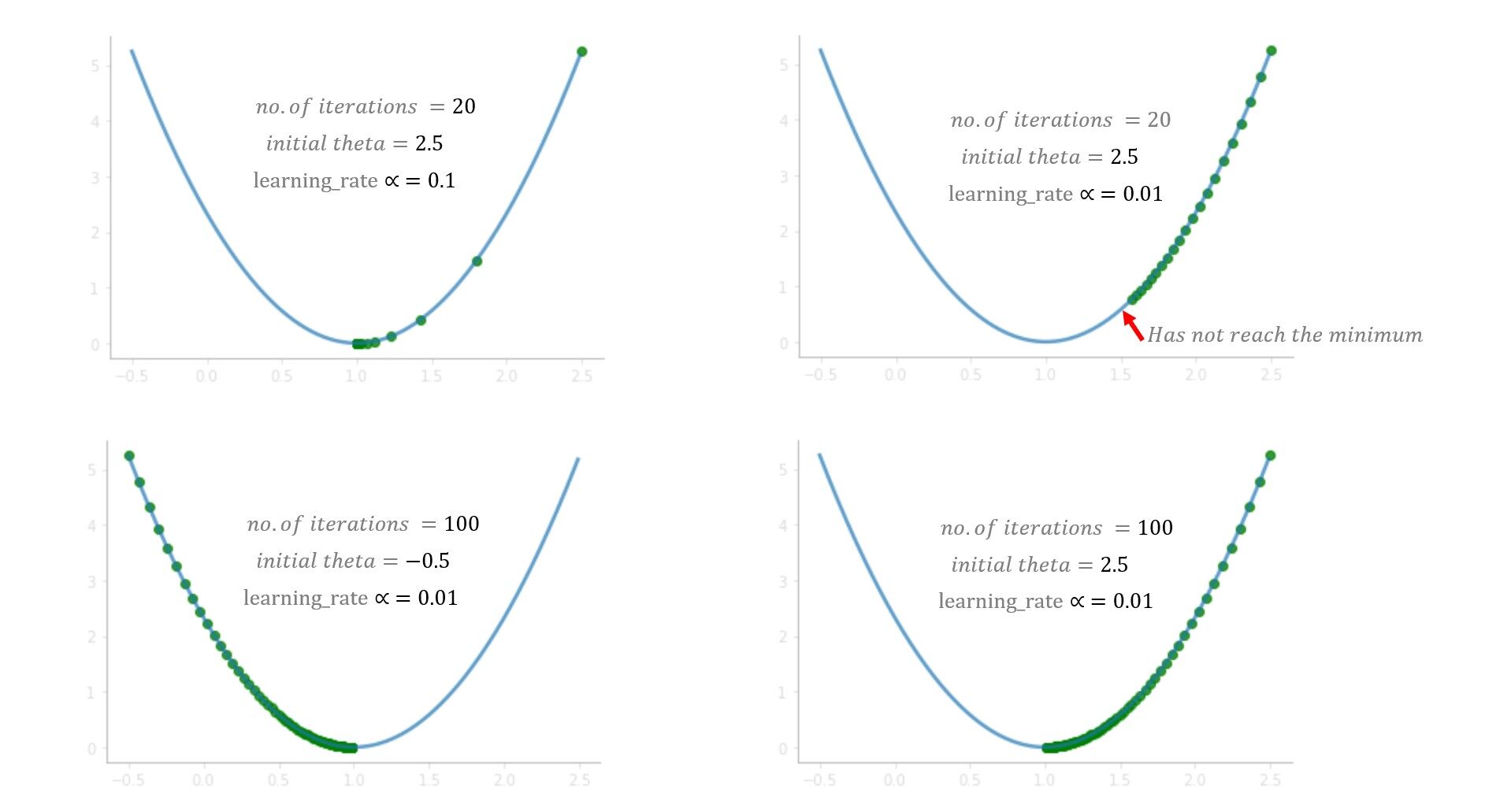
Cosa hai imparato dal gioco? All'inizio, provi un tasso di apprendimento (alfa) = 1 ma non raggiungi il minimo, perché i passi più grandi superano il minimo. Nella prossima partita, provi con alfa = 0.1, e questa volta sei riuscito ad arrivare in fondo in tutta sicurezza. E se avessi provato alfa = 0.01? Bene, poi, andrai gradualmente giù ma non raggiungerai il fondo, 20 i salti non bastano per arrivare in fondo con alpha = 0.01, 100 i salti potrebbero bastare. Mentre risolvi un problema del mondo reale, normalmente un alfa compreso tra 0,01 e 0,1 dovrebbe funzionare bene, ma varia con il numero di iterazioni che l'algoritmo richiede, alcuni problemi potrebbero richiedere 100 o anche 1000 iterazioni.

Sulla base di questi fattori, puoi provare diversi valori alfa. Sebbene la regolazione del valore alfa sia uno dei compiti importanti per comprendere l'algoritmo, Ti suggerisco di guardare altre parti dell'algoritmo oltre alle parti derivate, il segno meno, aggiorna i parametri e capisci quali sono i ruoli dei tuoi individui.

Discesa del gradiente di codifica

Fino ad ora, stiamo usando un solo parametro per calcolare la funzione di costo e gli algoritmi. Che aspetto ha la funzione di costo e come funziona l'algoritmo quando abbiamo due o più parametri? Vedere la figura sotto per una comprensione intuitiva. Immagina di essere da qualche parte sulla cima della montagna e di lottare per scendere alla base della montagna con gli occhi bendati..

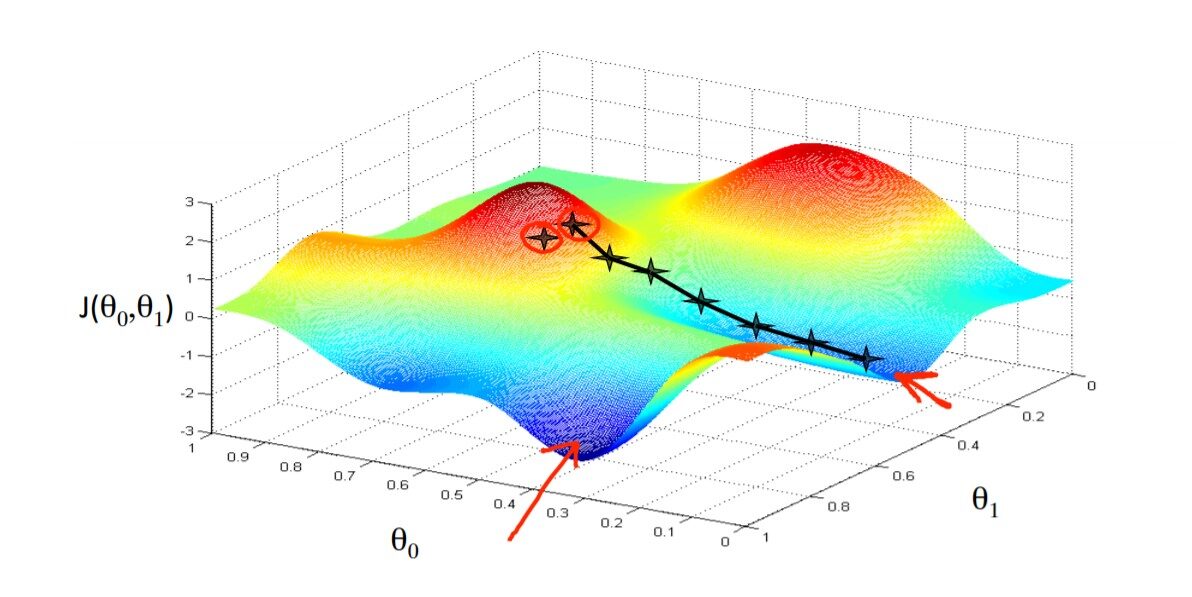
Il principio di funzionamento dell'algoritmo è lo stesso per qualsiasi numero di parametri, è solo che più sono i parametri più è la direzione della pendenza. Nell'esempio sopra della curva a forma di ciotola, dobbiamo solo osservare la pendenza di theta1, ma ora l'algoritmo deve guardare in entrambe le direzioni per minimizzare la funzione di costo. Codifichiamo e comprendiamo l'algoritmo. Si prega di fare riferimento alla figura sottostante per riferimento:

Eccoci qui, il nostro modello prevede 475,88 * 1000 = $ 475,880 per le dimensioni della casa 3 * 1000 piedi quadrati. È molto vicino alla nostra previsione che abbiamo fatto all'inizio usando la nostra intuizione.

conclusione

Come principiante, può essere un po' difficile capire tutti i concetti di regressione lineare in un tempo di lettura così breve. Non direi che sai tutto sulla regressione lineare da questo articolo. Lo scopo di questo articolo è rendere gli algoritmi comprensibili nel modo più semplice possibile. Segui il collegamento alla risorsa di seguito per una migliore comprensione. Spero ti sia piaciuto leggere l'articolo. Grazie per aver letto.