Simulazione Monte Carlo | Esegui la simulazione Monte Carlo in R

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati.

introduzione

Questo articolo si propone di presentare la simulazione Monte Carlo per l'analisi dell'incertezza variabile. Monte Carlo può sostituire la propagazione dell'errore perché supera gli svantaggi della propagazione dell'errore.. noi discuteremo:

• Come eseguire la propagazione degli errori;
• Perché usare Monte Carlo invece della propagazione degli errori? e
• I passi per realizzare l'incertezza di Montecarlo.

Iniziamo questa discussione con cose semplici. Quanto spende un impiegato della città A per le spese di soggiorno in un mese? Ci sono migliaia di dipendenti nella città A con spese di soggiorno diverse. Per rispondere alla domanda precedente, dobbiamo chiedere a diversi dipendenti e registrare le loro risposte. Quei dipendenti risponderanno in modo diverso. Le tue spese di soggiorno varieranno lungo una distribuzione di probabilità. Anche se non abbiamo le risorse per chiedere a tutti i dipendenti, possiamo campionare un gruppo di, ad esempio, 50 dipendenti in modo che l'indagine rappresenti la popolazione.

tuttavia, abbiamo ancora bisogno di un numero per rappresentare la spesa totale del soggiorno. Diciamo che otteniamo la spesa media mensile per essere $ 2000. Oh bene, un altro modo è utilizzare la mediana per rappresentare la spesa totale. Per esprimere altre possibili spese di soggiorno, possiamo usare la deviazione standard. Ad esempio, il costo della vita mensile nella città A è $ 2000 ± 500 (media ± deviazione standard).

Significa che se i dati sono normalmente distribuiti, il 68,2% dei dipendenti trascorrono tra $ 1500 e $ 2500. Ce n'è un altro 31,8% dei dipendenti che spendono meno di $ 1500 e altro ancora $ 2500 nel costo della vita mensile. La probabilità di spesa per vivere diminuisce man mano che si allontana dalla media. C'è una probabilità di 0,1% di trovare dipendenti con spese di soggiorno inferiori $ 500 o superiore a $ 3500. La deviazione standard riflette l'incertezza variabile del costo della vita. Indica l'estensione inferiore e superiore della variabile, invece di fare affidamento su un unico valore.

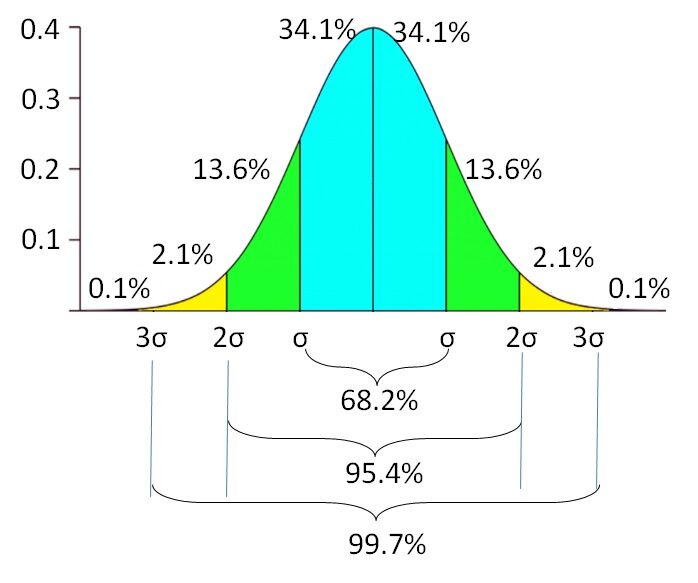
propagazione dell'errore

Poiché i dipendenti della città A hanno un reddito: $ 3200 ± 2000, spese di soggiorno: $ 2000 ± 500, credito: $ 180 ± 130, entrate o spese impreviste: $ 20 ± 300 e tasso di interesse bancario: 0,85 ± 0,35% mensile. Vogliamo calcolare quanto può risparmiare un dipendente in un mese. L'equazione è espressa di seguito:

risparmio = (Reddito – Spese di soggiorno – Credito + Reddito / spese impreviste) × (1 + Interessi)

Il risparmio mensile viene calcolato come reddito totale dedotto dalle spese di soggiorno e dal credito e aggiunto a eventuali entrate o spese impreviste. Dopo un mese, aumento del risparmio nominale dovuto agli interessi bancari. Calcoleremo il risparmio medio mensile e l'incertezza. Osserva la seguente equazione su come calcolare l'incertezza.

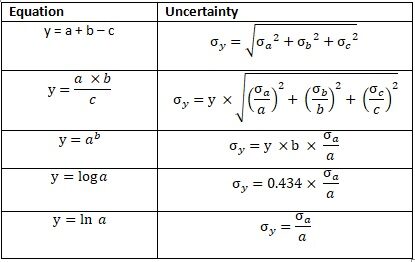
Fig.2 Propagazione dell'errore

Salvataggio1 = ((3200 ± 2000) - (2000 ± 500) - (180 ± 130) + (20 ± 300)) × (1 + (0.0085 ± 0.0035))

Salvataggio1 = 1040 ± σRisparmio_1

?Risparmio_1 = ((20002 + 5002 + 1302 + 20002))0.5

?Risparmio_1 = 2087

Risparmio1 ± σRisparmio_1 = 1040 ± 2087

Questo calcola il risparmio mensile dopo aver contabilizzato gli interessi bancari.

Salvataggio = Salvataggio1 × (1 + (0.0085 ± 0.0035)) 

Salvataggio = (1040 ± 2087) × (1.0085 ± 0.0035)

Salvataggio = 1049 ± σRisparmio_2

?Salvataggio = 1049 × ((2087/1040)2 + (0.0035/1.0085)2)0.5

?Salvataggio = 1049 × 2.01

?Salvataggio = 2105

Risparmio ± σ_Salvataggio = 1049 ± 2105

Dal risultato, possiamo vederlo, in media, le persone possono risparmiare $ 1049 tra un mese con l'incertezza di $ 2105. Il limite inferiore del risparmio mensile è – $ 1056 ($ 1049 – $ 2105), che è un valore negativo. L'incertezza stessa lo è 2105, Che cos'è 2 volte maggiore del valore medio. Se osserviamo il grafico, possiamo vedere che i risparmi dei dipendenti vanno da – $ 6000 e $ 8000. Sembra strano perché i limiti inferiore e superiore sono quasi bilanciati. penso che, in realtà, l'importo del risparmio dovrebbe avere una variabilità maggiore dell'importo del disavanzo.

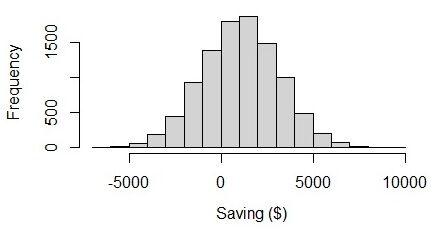
Fig.3 Visualizzazione del risparmio in una distribuzione normale

come sta succedendo? Il problema è nei dati sul reddito. Il reddito di $ 3200 ± 2000 presenta un'elevata incertezza a causa della variabilità del reddito. L'incertezza è più di un terzo del valore medio. Se assumiamo che questa sia una distribuzione normale, vedremo che il 4.8% della popolazione ha un reddito inferiore 0, cosa che non sembra probabile che accada. Infatti, il reddito deve essere sempre superiore alla % 0. Questo problema si verifica quando assumiamo che tutte le variabili siano distribuite normalmente., ma in realtà non lo sono.

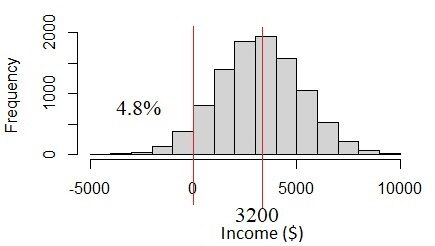
Fig.4 Distribuzione normale se la deviazione standard del reddito è troppo grande

Simulazione Monte Carlo

Qual'è la soluzione? Un altro modo per valutare l'incertezza è applicare la simulazione Monte Carlo. Monte Carlo è originariamente il nome di un'area amministrativa di Monaco. Ma il Monte Carlo della nostra discussione oggi è roba statistica.. Monte Carlo può superare lo svantaggio della propagazione dell'errore. La simulazione Monte Carlo, a differenza della propagazione dell'errore, può lavorare su una distribuzione di dati diversa dalla distribuzione normale e su dati con una deviazione standard elevata.

Fig.5 Montecarlo a Monaco. Fonte: Google Map

La simulazione Monte Carlo simula o genera un insieme di numeri casuali in base alla distribuzione dei dati e ai parametri di ciascuna variabile. Una volta generato, tutti i valori delle variabili vengono calcolati utilizzando l'equazione. Questo suona un po' più complicato rispetto all'utilizzo della propagazione degli errori. Ma usa gli strumenti della scienza dei dati, come Python o R, sarà molto semplice. in questa discussione, dimostreremo l'uso del linguaggio statistico R.

Passaggi per eseguire una simulazione Monte Carlo

1. Controllare la funzione di densità di probabilità della distribuzione dei dati.

Diciamo che esaminiamo il record di dati fornito dal sondaggio di 50 intervistato. Esistono molti tipi di funzioni di densità di probabilità e dobbiamo determinare quale si adatta ai nostri dati.. Le variabili normalmente distribuite sono solo spese di soggiorno e entrate o spese impreviste. La distribuzione dei dati sul reddito è positiva.

In questo caso, lo tratteremo come una distribuzione gamma. Questo è il motivo per cui la media e la propagazione dell'errore non sono adatte per questi dati.. Anche le altre due variabili non hanno una distribuzione normale.. Il tasso di interesse bancario è distribuito uniformemente 0,3 e 1,5.

La distribuzione dei dati sui prestiti per estinguere il credito è piuttosto singolare. I dati sono distribuiti principalmente in due gruppi di popolazione. Il primo gruppo ha meno credito del secondo. Diciamo che la distribuzione dei dati sul credito non si adatta a nessuna funzione di densità di probabilità. Dopo, useremo una distribuzione non parametrica.

2. Genera simulazione Monte Carlo

Generare una simulazione Monte Carlo significa generare un insieme di numeri casuali con la stessa distribuzione dei dati dei dati originali.. Per fare questo, impostiamo semplicemente il numero di simulazioni ei parametri di distribuzione in base al tipo di distribuzione. Impostiamo il numero di simulazioni su 10,000. Significa che simuleremo i dati di 50 intervistato in 10,000 dati.

I parametri della distribuzione normale sono medi / media e deviazione standard. Sappiamo che le medie ± deviazioni standard delle spese di soggiorno e entrate o risultati imprevisti lo sono 2000 ± 500 e 20 ± 300 rispettivamente. Ora, possiamo generare le distribuzioni. In questo articolo, Userò il linguaggio R. Certo, altri linguaggi della scienza dei dati, come Python, possono anche loro. Vedi che i dati simulati hanno una media e uno standard simili, non lo stesso, che i parametri di input.

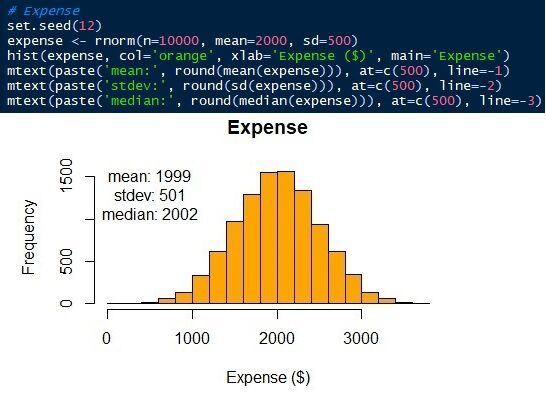
Fig.6 Distribuzione normale delle spese di soggiorno

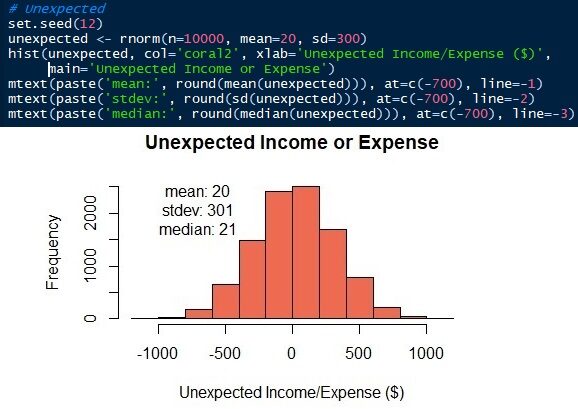
Fig.7 Distribuzione normale di entrate o spese impreviste

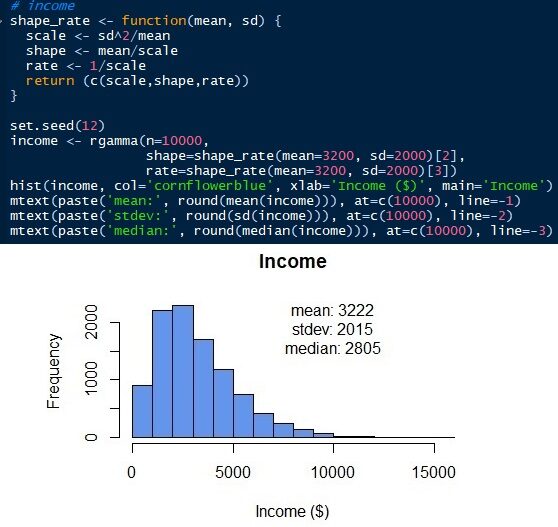
Per generare la distribuzione gamma, abbiamo bisogno di conoscere altri parametri. A differenza della distribuzione normale, la distribuzione gamma ha scala, forma e velocità come parametri. Ma possiamo ottenere quei parametri con la media e la deviazione standard (a partire dal). Scala = sd²/significare. forma = media / scala. Tasso = 1 / scala. Dopo, possiamo simulare la distribuzione gamma dei guadagni dei dipendenti come mostrato di seguito. La distribuzione gamma può avere solo valori positivi. Non c'è alcun valore sotto 0 poiché il reddito di tutti i dipendenti deve essere un numero positivo. La distribuzione normale darebbe valori negativi se l'errore standard è troppo grande.. Si noti che la distribuzione simulata ha una media e una deviazione standard di 3222 e 2015 rispettivamente, che sono vicini ai parametri di input originali. Ma abbiamo una mediana di 2805. La mediana della distribuzione gamma, a differenza della distribuzione normale, è lontano dalla media.

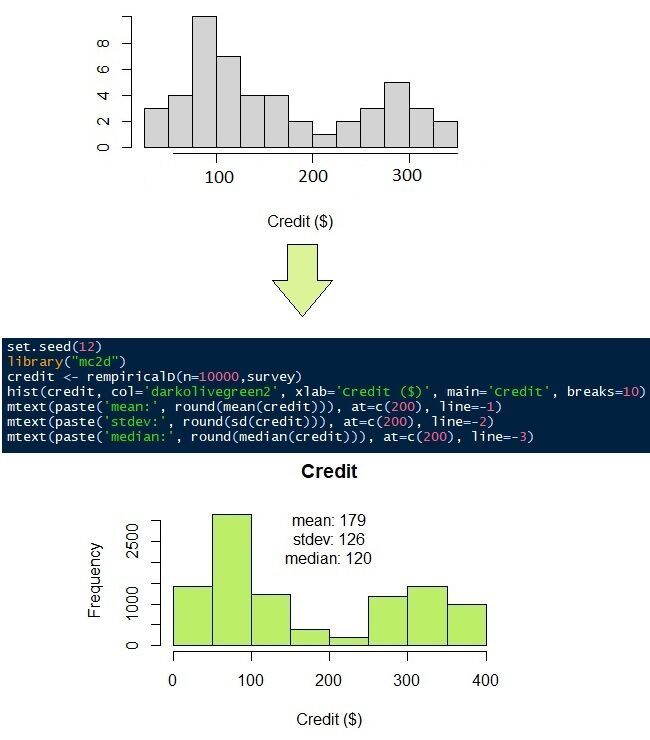
Credito da pagare mensilmente, come menzionato prima, non ha una funzione di densità di probabilità adeguata. Dai un'occhiata alle risposte di 50 sondaggi in figura 9 (istogramma grigio). Sembra che la maggior parte delle persone debba ripagare il proprio credito $ 100 e $ 300. Per simulare il 50 osservazioni su 10,000 osservazioni, possiamo usare una distribuzione non parametrica. Come suggerisce il nome, la distribuzione non parametrica non richiede parametri, come la media, la deviazione standard, il modulo o la tariffa, così come le distribuzioni normale e gamma. Richiede solo i dati originali.

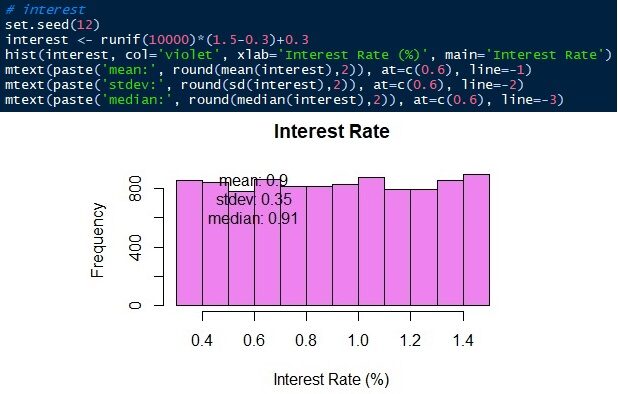
L'ultima variabile da simulare è il tasso di interesse bancario. Il tasso di interesse bancario varia da 0,3 un 1,5 uniformemente. Facciamo lo stesso 10,000 osservazioni che vanno da 0.3 un 1.5 con la stessa probabilità.

3. Combinazione di simulazioni Monte Carlo

L'ultimo passaggio consiste nel combinare le simulazioni Monte Carlo utilizzando l'equazione per calcolare il risparmio mensile. Per fare questo, dobbiamo solo mettere insieme tutte le simulazioni in una tabella. Dopo, possiamo calcolare 10,000 righe di risparmio mensile. Il risultato è $ 1073 ± 2052, non troppo diverso dalla propagazione dell'errore. Ma, La simulazione Monte Carlo mostra la densità di probabilità. Possiamo vedere che il risparmio medio è $ 666 e gli intervalli di dati da $ 2000 e 10000.

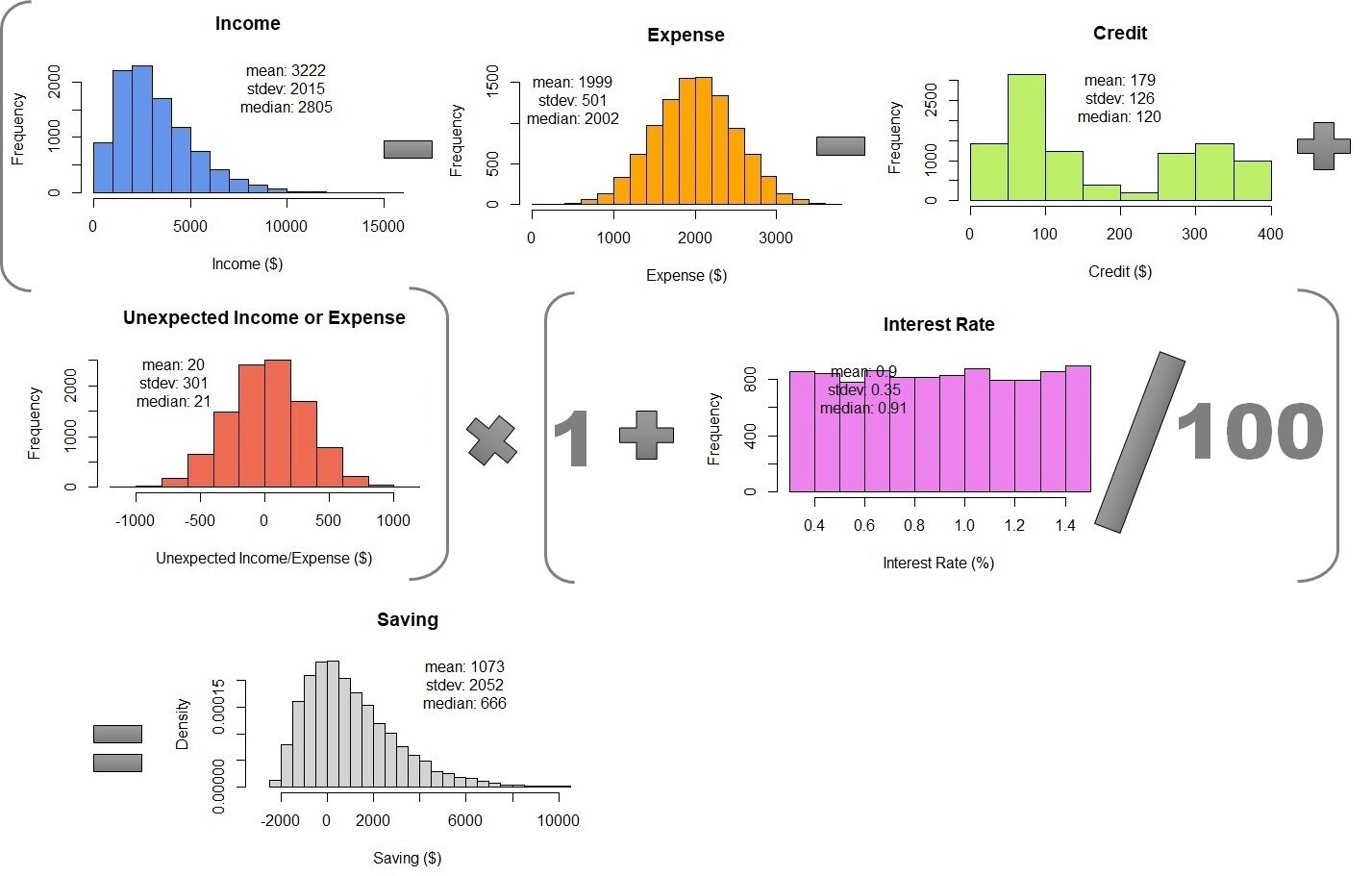
Tavolo 1 – Combinazione di simulazioni Monte Carlo

Ora, Vediamo un altro esempio con variabilità spaziale e temporale. Il compito è calcolare il deflusso superficiale di un bacino. Il bacino è il limite dell'idrologia delle acque superficiali. Tutta la pioggia che cade al di sotto del bacino non attraverserà il confine. Parte della pioggia si infiltra nel terreno in base alla dimensione delle particelle di terreno e al tipo di copertura del suolo.. L'acqua che non si infiltra nel terreno è chiamata deflusso superficiale.. Il deflusso superficiale scorrerà nel fiume come scarico del fiume.

La tabella seguente mostra l'intensità delle precipitazioni mensili in un anno e il coefficiente di deflusso in un anno. 1,5 km.² cuenca. L'incertezza può essere dovuta all'eterogeneità spaziale e temporale. Il coefficiente di precipitazione e deflusso (a causa del tipo di suolo e di copertura del suolo) varia spazialmente nel bacino. Le precipitazioni del bacino vengono misurate con diversi pluviometri. Danno precipitazioni medie con incertezza dovuta alla distribuzione spaziale. La distribuzione della copertura del suolo fornisce anche l'incertezza del coefficiente di deflusso.

Un coefficiente di deflusso è la proporzione di pioggia che non si infiltra nel suolo e diventa deflusso superficiale.. Il tipo di terreno forestale o grossolano ha un basso coefficiente di deflusso. Gli insediamenti o le case hanno un alto coefficiente di deflusso. La conversione della copertura forestale in insediamenti aumenta il coefficiente di deflusso perché una percentuale maggiore di acqua piovana sarà di deflusso superficiale..

La variabilità temporale si verifica anche perché le precipitazioni nelle stagioni umide e secche sono diverse.. Il cambiamento della copertura del suolo nel tempo causa anche variabilità temporale del coefficiente di deflusso. Altre fonti di incertezza sono la qualità degli strumenti di misurazione, metodi di misurazione, condizioni ambientali e altre condizioni inspiegabili dovute alla mancanza di conoscenza.

Mio	precipitazione (mm / mio)	coefficiente di deflusso	La zona (km2)
uno	320 ± 37	0,3 ± 0,2	1,5
febbraio	350 ± 59	0,3 ± 0,2	1,5
mar	205 ± 26	0,4 ± 0,1	1,5
aprile	170 ± 41	0,4 ± 0,1	1,5
Mayo	106 ± 48	0,4 ± 0,1	1,5
giu	91 ± 32	0,4 ± 0,1	1,5
lug	77 ± 16	0,4 ± 0,1	1,5
fa	52 ± 15	0,7 ± 0,2	1,5
settembre	100 ± 50	0,7 ± 0,2	1,5
ott	120 ± 46	0,7 ± 0,2	1,5
novembre	253 ± 45	0,7 ± 0,2	1,5
dic	210 ± 48	0,7 ± 0,2	1,5

L'equazione è deflusso superficiale = tasso di precipitazione × coefficiente di deflusso × bacino idrografico. L'intera distribuzione viene simulata utilizzando una distribuzione gamma. Il deflusso medio mensile di superficie è 124.000 ± 30 m³/mio. La mediana è 120.000 m³/mio.

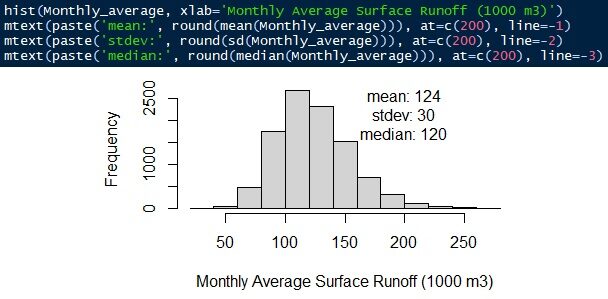
Fig.12 Deflusso superficiale medio mensile

Circa l'autore

Connettiti con me qui https://www.linkedin.com/in/rendy-kurnia/

Imparentato