Test statistici | Selezione delle funzioni mediante test statistici

Questo articolo è stato pubblicato nell'ambito del Blogathon sulla scienza dei dati

introduzione

La selezione delle funzionalità è il processo di selezione delle funzionalità rilevanti per un modello di machine learning. Significa che seleziona solo quegli attributi che hanno un effetto significativo sull'output del modello.

Prendi in considerazione il caso in cui vai al grande magazzino per acquistare prodotti alimentari. Un prodotto ha molte informazioni, vale a dire, Prodotto, categoria, scadenza, MRP, ingredienti e dettagli di fabbricazione. Tutte queste informazioni sono le caratteristiche del prodotto. Normalmente, controlla il marchio, MRP e data di scadenza prima di acquistare un prodotto. tuttavia, la sezione ingredienti e produzione non ti riguarda. Perciò, la marca, el mrp, la data di scadenza sono le caratteristiche rilevanti e l'ingrediente, i dettagli di produzione sono irrilevanti. Ecco come viene eseguita la selezione delle funzionalità.

Nel mondo reale, un set di dati può avere migliaia di funzionalità e potrebbero esserci possibilità che alcune funzionalità siano ridondanti, alcuni potrebbero essere correlati e alcuni potrebbero essere irrilevanti per il modello. In questa fase, se usi tutte le funzioni, ci vorrà molto tempo per addestrare il modello e la precisione del modello sarà ridotta. Perciò, la selezione delle caratteristiche diventa importante nella costruzione del modello. Esistono molti altri modi per selezionare le funzionalità, come eliminazione di caratteristiche ricorsive, algoritmi genetici, alberi decisionali. tuttavia, Ti dirò il metodo di filtraggio più semplice e manuale usando i test statistici.

Ora che hai una conoscenza di base della selezione delle funzioni, vedremo come implementare vari test statistici sui dati per selezionare caratteristiche importanti.

obbiettivo

L'obiettivo principale di questo blog è comprendere i test statistici e la loro implementazione in dati reali in Python, che aiuterà nella selezione delle caratteristiche.

Terminologie

Prima di addentrarci nei tipi di test statistici e nella loro implementazione, è necessario comprendere i significati di alcune terminologie.

Verifica di ipotesi

Il test di ipotesi nelle statistiche è un metodo per testare i risultati di esperimenti o sondaggi per vedere se ha risultati significativi.. Utile quando si desidera inferire su una popolazione basata su un campione o una correlazione tra due o più campioni.

Ipotesi nullaLa hipótesis nula es un concepto fundamental en la estadística que establece una afirmación inicial sobre un parámetro poblacional. Su propósito es ser probada y, en caso de ser refutada, permite aceptar la hipótesis alternativa. Este enfoque es esencial en la investigación científica, ya que proporciona un marco para evaluar la evidencia empírica y tomar decisiones basadas en datos. Su formulación y análisis son cruciales en estudios estadísticos....

Questa ipotesi stabilisce che non vi è alcuna differenza significativa tra campione e popolazione o tra popolazioni diverse.. È indicato con H₀.

Non. Supponiamo che la media di 2 i campioni sono gli stessi.

Ipotesi alternativa

L'affermazione contraria all'ipotesi nulla è inclusa nell'ipotesi alternativa. È indicato con H₁.

Non. Assumiamo che la media di 2 i campioni non sono uniformi.

valore critico

È un punto sulla scala della statistica test oltre il quale l'ipotesi nulla viene respinta.. Più alto è il valore critico, minore è la probabilità che 2 i campioni appartengono alla stessa distribuzione. Il valore critico per qualsiasi test può

valore p

p-value significa "valore di probabilità"; indica la probabilità che un esito si sia verificato per caso. Fondamentalmente, il valore p viene utilizzato nei test di ipotesi per aiutarti a supportare o rifiutare l'ipotesi nulla. Più piccolo è il p-value, più forte è l'evidenza per rifiutare l'ipotesi nulla.

Grado di libertà

Il grado di libertà è il numero di variabili indipendenti. Questo concetto viene utilizzato per calcolare la statistica t e la statistica chi-quadrato.

Puoi fare riferimento a statistichewho.com per maggiori informazioni su queste terminologie.

Test statistici

Una prueba estadística es una forma de determinar si la variabileIn statistica e matematica, un "variabile" è un simbolo che rappresenta un valore che può cambiare o variare. Esistono diversi tipi di variabili, e qualitativo, che descrivono caratteristiche non numeriche, e quantitativo, che rappresentano quantità numeriche. Le variabili sono fondamentali negli esperimenti e negli studi, poiché consentono l'analisi delle relazioni e dei modelli tra elementi diversi, facilitare la comprensione di fenomeni complessi.... aleatoria sigue la hipótesis nula o la hipótesis alternativa. Fondamentalmente, dice se il campione e la popolazione o due o più campioni hanno differenze significative. Puoi usare varie statistiche descrittive come media, medianoLa mediana è una misura statistica che rappresenta il valore centrale di un insieme di dati ordinati. Per calcolarlo, I dati sono organizzati dal più basso al più alto e viene identificato il numero al centro. Se c'è un numero pari di osservazioni, I due valori fondamentali sono mediati. Questo indicatore è particolarmente utile nelle distribuzioni asimmetriche, poiché non è influenzato da valori estremi...., modo, intervallo o deviazione standard per questo scopo. tuttavia, generalmente usiamo la media. Il test statistico ti dà un numero che viene poi confrontato con il p-value. Se il suo valore è maggiore del p-value, accettare l'ipotesi nulla, altrimenti, lei rifiuta.

La procedura per implementare ciascun test statistico sarà la seguente:

• Calcoliamo il valore statistico utilizzando la formula matematica
• Quindi calcoliamo il valore critico utilizzando tabelle statistiche.
• Con l'aiuto del valore critico, calcoliamo il p-value
• Se il p-value> 0.05 accettiamo l'ipotesi nulla, altrimenti lo rifiutiamo

Ora che hai compreso la selezione delle funzionalità e i test statistici, possiamo muoverci verso l'implementazione di vari test statistici insieme al loro significato. Prima di ciò, ti mostrerò il set di dati e questo set di dati verrà utilizzato per tutti i test.

Set di dati

Il set di dati che utilizzerò è un set di dati di previsione del prestito che è stato preso dal concorso di analisi Vidhya. Puoi anche partecipare al concorso e scaricare il set di dati. qui.

Per prima cosa ho importato tutti i moduli Python necessari e il set di dati.

importa numpy come np
importa panda come pd
import seaborn come sb
da numpy import sqrt, addominali, il giro
importa scipy.stats come statistiche
da scipy.stats importa la norma
df=pd.read_csv('prestito.csv')
df.head()

Ci sono molte caratteristiche nel set di dati, come genere, dipendenti, formazione scolastica, reddito del richiedente, ammontare del prestito, storia creditizia. Utilizzeremo queste funzionalità e verificheremo se un effetto di una funzionalità influisce su altre funzionalità utilizzando vari test, vale a dire, Prova Z, test di correlazione, Test ANOVA e test Chi-quadro.

Prova Z

Un test Z viene utilizzato per confrontare la media di due campioni dati e dedurre se appartengono o meno alla stessa distribuzione.. Non implementiamo il test Z quando la dimensione del campione è inferiore a 30.

Un test Z può essere un test Z a un campione o un test Z a due campioni.

Il campione unico prova t determina se la media campionaria è statisticamente diversa da una media della popolazione nota o ipotizzata. Il test Z a due campioni confronta 2 variabili indipendenti.

Implementeremo un test Z a due campioni.

La statistica Z è indicata da

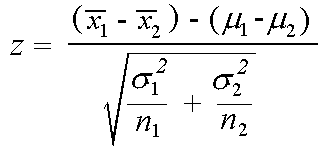
Implementazione

Si prega di notare che implementeremo 2 test di esempio z in cui una variabile sarà categorica con due categorie e l'altra variabile sarà continua per applicare il test z.

Qui useremo il Genere variabile categoriale e Reddito del richiedente Variabile continua. Il genere ha 2 gruppi: maschio e femmina. Quindi l'ipotesi sarà:

Ipotesi nulla: Non vi è alcuna differenza significativa tra il reddito medio di uomini e donne.

Ipotesi alternativa: c'è una differenza significativa tra il reddito medio di uomini e donne.

Codice

M_mean=df.loc[df['Genere']=='Uomo','Richiedente Reddito'].Significare()
F_mean=df.loc[df['Genere']=='Femmina','Richiedente Reddito'].Significare()
M_std=df.loc[df['Genere']=='Uomo','Richiedente Reddito'].standard()
F_std=df.loc[df['Genere']=='Femmina','Richiedente Reddito'].standard()
no_of_M=df.loc[df['Genere']=='Uomo','Richiedente Reddito'].contare()
no_of_F=df.loc[df['Genere']=='Femmina','Richiedente Reddito'].contare()

Il codice sopra calcola il reddito medio dei candidati di sesso maschile, il reddito medio delle donne richiedenti, la sua deviazione standard e il numero di campioni di uomini e donne.

dueSampZ La función calculará la estadística z y el valor p sin pasar por los parametriIl "parametri" sono variabili o criteri che vengono utilizzati per definire, misurare o valutare un fenomeno o un sistema. In vari campi come la statistica, Informatica e Ricerca Scientifica, I parametri sono fondamentali per stabilire norme e standard che guidano l'analisi e l'interpretazione dei dati. La loro corretta selezione e gestione sono fondamentali per ottenere risultati accurati e pertinenti in qualsiasi studio o progetto.... de entrada calculados anteriormente.

def dueSampZ(X1, X2, mudiff, sd1, sd2, n1, n2):
    pooledSE = sqrt(sd1**2/n1 + sd2**2/n2)
    z = ((X1 - X2) - mudiff)/raggruppatoSE
    pval = 2*(1 - norma.cdf(addominali(Insieme a)))
    torna indietro(Insieme a,3), pval
z,p= dueSampZ(M_significa,F_significa,0,M_std,F_std,no_of_M,no_of_F)
Stampa('Z'= z,'p'= p)

Z = 1.828

p = 0.06759726635832197

se p<0.05:
    Stampa("rifiutiamo l'ipotesi nulla")
altro:
    Stampa("accettiamo ipotesi nulla")

accettiamo l'ipotesi nulla

Poiché il valore p è maggiore di 0.5 accettiamo l'ipotesi nulla. Perciò, concludiamo che non vi è alcuna differenza significativa tra il reddito di uomini e donne.

Prova T

Un t-test viene anche utilizzato per confrontare la media di due campioni dati., come il test Z. tuttavia, viene implementato quando la dimensione del campione è inferiore a 30. Si assume una distribuzione normale del campione. Può anche essere uno o due campioni. Il grado di libertà è calcolato da n-1 dove n è il numero di campioni.

È indicato da

Implementazione

Sarà implementato allo stesso modo del test Z. L'unica condizione è che la dimensione del campione deve essere inferiore a 30. Ti ho mostrato l'implementazione del test Z. Ora, puoi provare il T-Test.

Test di correlazione

Un test di correlazione è una metrica per valutare la misura in cui le variabili sono associate tra loro.

Si noti che le variabili devono essere continue per applicare il test di correlazione.

Esistono diversi metodi per i test di correlazione, vale a dire, covarianza, Coefficiente di correlazione di Pearson, Coefficiente di correlazione di rango di Spearman, eccetera.

Useremo il coefficiente di correlazione delle persone poiché è indipendente dai valori delle variabili.

Coefficiente di correlazione di Pearson

Viene utilizzato per misurare la correlazione lineare tra 2 variabili. È indicato da

Immagine google

I suoi valori sono compresi tra -1 e 1.

Se il valore di r è 0, significa che non c'è relazione tra le variabili X e Y.

Se il valore di r è compreso tra 0 e 1, significa che esiste una relazione positiva tra X e Y, e la sua forza aumenta da 0 un 1. Relazione positiva significa che se il valore di X aumenta, aumenta anche il valore di Y.

Se il valore di r è compreso tra -1 e 0, significa che esiste una relazione negativa tra X e Y, e la sua forza diminuisce da -1 un 0. Relazione negativa significa che se il valore di X aumenta, il valore di Y diminuisce.

Implementazione

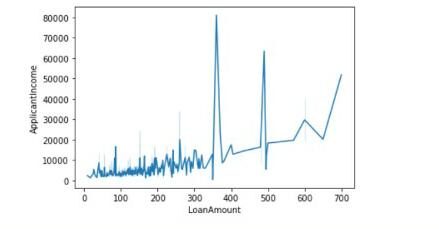
Qui useremo due variabili o caratteristiche continue: Ammontare del prestito e Reddito del richiedente. Concluderemo se esiste una relazione lineare tra l'importo del prestito e il reddito del richiedente con il valore del coefficiente di correlazione di Pearson e tracciamo anche il grafico tra di loro.

Codice

Ci sono alcuni valori mancanti nella colonna LoanAmount, primo, lo riempiamo con il valore medio. Poi ha calcolato il valore del coefficiente di correlazione.

df['Ammontare del prestito']= df['Ammontare del prestito'].riempire (df['Ammontare del prestito'].significare())

pcc = ad esempio corrcoef (df.ApplicantIncome, df.LoanAmount)

stampare (pcc)

[[1.         0.56562046]
 [0.56562046 1.        ]]

I valori delle diagonali indicano la correlazione delle caratteristiche con se stesse. 0.56 rappresentano che c'è qualche correlazione tra le due caratteristiche.

Possiamo anche disegnare il grafico come segue:

sns.lineplot(dati=df,x='Importo Prestito',y = 'Richiedente Reddito')

ANOVA test

ANOVA significa Analisi della varianza. Come suggerisce il nome, usa la varianza come parametro per confrontare più gruppi indipendenti. ANOVA può essere ANOVA unidirezionale o ANOVA bidirezionale. L'ANOVA unidirezionale viene applicata quando ci sono tre o più gruppi indipendenti di una variabile. Implementeremo lo stesso in Python.

La statistica F può essere calcolata da

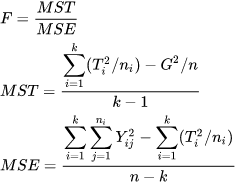
Implementazione

Qui useremo il dipendenti variabile categoriale e Reddito del richiedente Variabile continua. I dipendenti hanno 4 gruppi: 0,1,2,3+. Quindi l'ipotesi sarà:

Ipotesi nulla: Non vi è alcuna differenza significativa tra il reddito medio tra i diversi gruppi di persone a carico.

Ipotesi alternativa: c'è una differenza significativa tra il reddito medio tra i diversi gruppi di persone a carico.

Codice

Primo, gestiamo i valori mancanti nella funzione Dipendenti.

df['dipendenti'].è zero().somma()
df['dipendenti']=df['dipendenti'].riempire('0')

Dopo di che, creiamo un data frame con le caratteristiche Dependents e RichiedentIncome. Dopo, con l'aiuto della libreria scipy.stats, calcoliamo la statistica F e il p-value.

df_anova = df[['fattura_totale','giorno']]
grps = pd.unique(df.day.values)
d_data = {grp:df_anova['fattura_totale'][df_anova.day == grp] per grp in grps}
F, p = stats.f_oneway(d_data['Sole'], d_data['Sab'], d_data['gio'],d_data["ven"])

Stampa('F ={},p={}'.formato(F,P))

F =5.955112389949444,p=0.0005260114222572804

e P <0,05:

stampare (“rifiuta l'ipotesi nulla”)

il riposo:

stampare (“accettare ipotesi nulla”)

Rifiuta ipotesi nulla.

Poiché il p-value è minore di 0.5 rifiutiamo l'ipotesi nulla. Perciò, concludiamo che c'è una differenza significativa tra il reddito dei vari gruppi di Dipendenti.

Test del chi quadrato

Questo test viene applicato quando si hanno due variabili categoriali da una popolazione. Viene utilizzato per determinare se esiste un'associazione o una relazione significativa tra le due variabili.

Ci sono 2 tipi di test chi quadrato: bontà di adattamento chi-quadrato e test chi-quadrato per l'indipendenza, implementeremo quest'ultimo.

Il grado di libertà nel test chi-quadrato è calcolato da (n-1) * (m-1) dove n e m sono rispettivamente numeri di righe e colonne.

È indicato da:

Implementazione

Useremo le caratteristiche categoriche Genere e Stato del prestito e scopri se c'è un'associazione tra di loro usando il test chi-quadrato.

Ipotesi nulla: non esiste un'associazione significativa tra le caratteristiche di genere e lo stato del prestito.

Ipotesi alternativa: esiste un'associazione significativa tra le caratteristiche di genere e lo stato del prestito.

Codice

Primo, recuperiamo la colonna Gender e LoanStatus e formiamo un array.

dataset_table=pd.crosstab(set di dati['sesso'],set di dati['fumatore'])
dataset_table

Loan_Status  N  Y
Gender
Female      37   75
Maschio        33  339

Dopo, calcoliamo i valori osservati e attesi utilizzando la tabella sopra.

osservato=dataset_table.values
val2=stats.chi2_contingency(dataset_table)
atteso=val2[3]

Quindi calcoliamo la statistica chi-quadrato e il p-value usando il seguente codice:

da scipy.stats import chi2
chi_square=somma([(o-e)**2./e per o,e in zip(osservato,previsto)])
chi_square_statistic=chi_square[0]+chi_square[1]
p_value=1-chi2.cdf(x=chi_square_statistica,df = ddof)

Stampa("statistica chi-quadrato:-",chi_square_statistica)

Stampa("Livello di significatività": ',alfa)

Stampa('Grado di libertà: ',verrò)

Stampa('p-value:',p_value)

statistica chi-quadrato:- 0.23697508750826923
Livello di significatività:  0.05
Grado di libertà:  1
valore p: 0.6263994534115932

se p_value<=alfa:

    Stampa("Rifiuta l'ipotesi nulla")

altro:

    Stampa("Accetta l'ipotesi nulla")

Accetta l'ipotesi nulla

Poiché il valore p è maggiore di 0.05, accettiamo l'ipotesi nulla. Concludiamo che non vi è alcuna associazione significativa tra le due caratteristiche.

Riepilogo

Primo, abbiamo discusso della selezione delle funzionalità. Si passa poi ai test statistici e alle varie terminologie ad esso collegate.. Finalmente, abbiamo visto l'applicazione di test statistici, vale a dire, Prova Z, T test, test di correlazione, ANOVA e test Chi-quadrato insieme alla loro implementazione in Python.

Riferimenti

Immagine eccezionale – Immagine google

Statistiche – statistichewho.com

A proposito di me

Ciao! Soy Ashish Choudhary. Sto studiando B.Tech alla JC Bose University of Science and Technology. La scienza dei dati è la mia passione e sono orgoglioso di scrivere blog interessanti ad essa correlati. Sentiti libero di contattarmi su LinkedIn.

Il supporto mostrato in questo articolo non è di proprietà di DataPeaker e viene utilizzato a discrezione dell'autore.

Imparentato