Este artigo foi publicado como parte do Data Science Blogathon.
Introdução
Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA.. Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA.. Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA., Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA..
Para saber a sazonalidade, Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA..
Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA., Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA..
Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA.
Um método estatístico popular e amplamente utilizado para previsão de séries temporais é o modelo ARIMA., daí a série temporal com tendências, daí a série temporal com tendências, daí a série temporal com tendências. daí a série temporal com tendências. Por outro lado, daí a série temporal com tendências, daí a série temporal com tendências. Em geral, daí a série temporal com tendências.
daí a série temporal com tendências. daí a série temporal com tendências.
Neste tutorial, daí a série temporal com tendências.
daí a série temporal com tendências. É realmente simplificado em termos de uso. Porém, É realmente simplificado em termos de uso.
É realmente simplificado em termos de uso.
É realmente simplificado em termos de uso:
p: É realmente simplificado em termos de uso, É realmente simplificado em termos de uso.
d: É realmente simplificado em termos de uso, É realmente simplificado em termos de uso.
q: É realmente simplificado em termos de uso, É realmente simplificado em termos de uso.
É realmente simplificado em termos de uso, É realmente simplificado em termos de uso, quer dizer, eliminar tendência e estruturas sazonais que afetam negativamente o modelo de regressão.
PASSOS
1. Exibir dados da série time
2. Identifique se a data está parada
3. Plote os gráficos de correlação e correlação automática
4. Construa o modelo ARIMA ou ARIMA sazonal com base nos dados
Comecemos
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
Neste tutorial, Estou usando o seguinte conjunto de dados.
df = pd.read_csv('time_series_data.csv')
df.head()
# Updating the header
df.columns=["Mês","Vendas"]
df.head()
df.describe()
df.set_index('Mês',inplace = True)
from pylab import rcParams
rcParams['figure.figsize'] = 15, 7
df.plot()
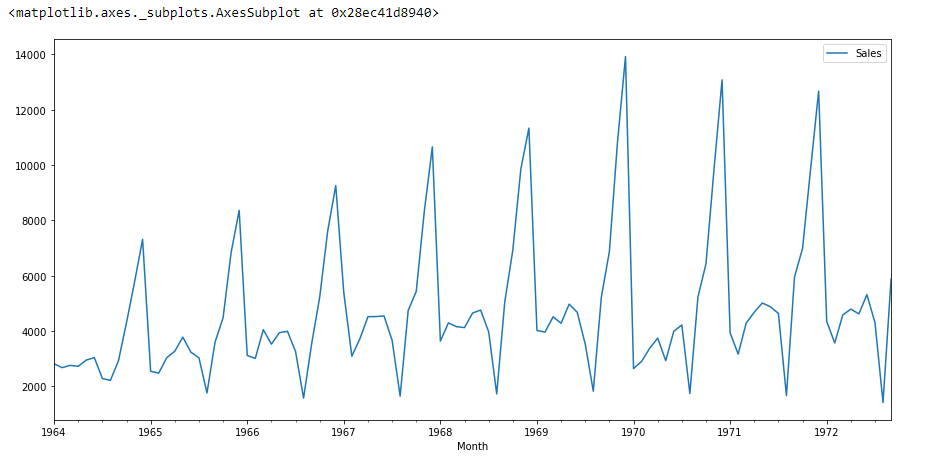
se olharmos para o gráfico acima, então podemos encontrar uma tendência de que há um momento em que as vendas são altas e vice-versa. Isso significa que podemos ver que os dados seguem a sazonalidade.. Para ARIMA, a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários. a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários, a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários.
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários, a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários.
de statsmodels.tsa.stattools import adfuller
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários.
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários(df['Vendas'])
Para identificar a natureza dos dados, vamos usar a hipótese nula.
H0: A hipótese nula: a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários.
H1: A hipótese alternativa: É uma afirmação sobre a população que contradiz H0 e o que concluímos quando rejeitamos H0.
#Ho: não é estacionário
# H1: está parado
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários.
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários(a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários):
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários(a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários)
a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários [a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários,a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários,a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários,a primeira coisa que fazemos é identificar se os dados são estacionários ou não estacionários]
por valor,rótulo em zip(resultado,rótulos):
imprimir(rótulo+' : '+str(valor) )
se resultado[1] <= 0.05:
imprimir("forte evidência contra a hipótese nula(Ho), rejeitar a hipótese nula. Os dados estão parados")
outro:
imprimir("evidência fraca contra hipótese nula,indicando que não está estacionário ")
adfuller_test(df['Vendas'])
Depois de executar o código acima, vamos obter o valor P,
Estatística de teste ADF : -1.8335930563276237 valor p : 0.3639157716602447 #Lags usados : 11 Número de Observações : 93
Aqui o valor P é 0.36, que é maior que 0.05, o que significa que os dados aceitam a hipótese nula, o que significa que os dados não são estacionários.
Vamos tentar ver a primeira diferença e a diferença sazonal:
df['Vendas Primeira Diferença'] = df['Vendas'] - df['Vendas'].mudança(1) df['Primeira Diferença Sazonal']= df['Vendas']-df['Vendas'].mudança(12) df.head()

# Again testing if data is stationary
adfuller_test(df['Primeira Diferença Sazonal'].derrubar())
Estatística de teste ADF : -7.626619157213163
valor p : 2.060579696813685e-11
#Lags Used : 0
Número de Observações : 92
Aqui o valor P é 2.06, o que significa que vamos rejeitar a hipótese nula. Em seguida, os dados estão estacionários.
df['Primeira Diferença Sazonal'].enredo()
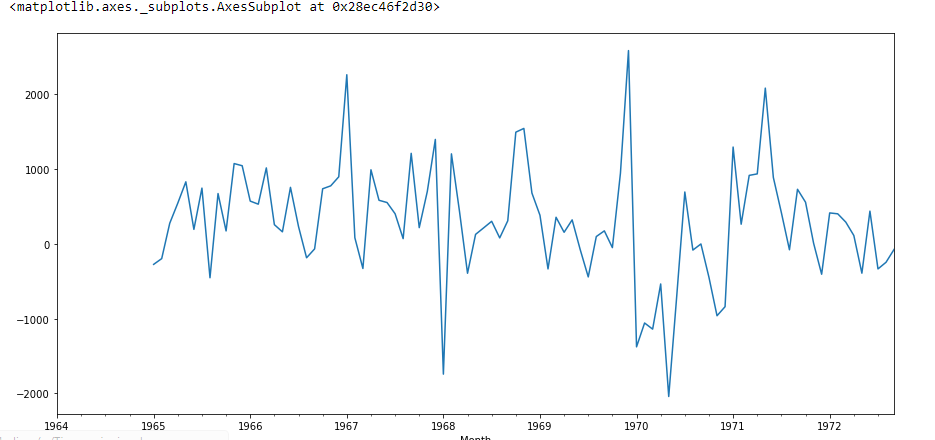
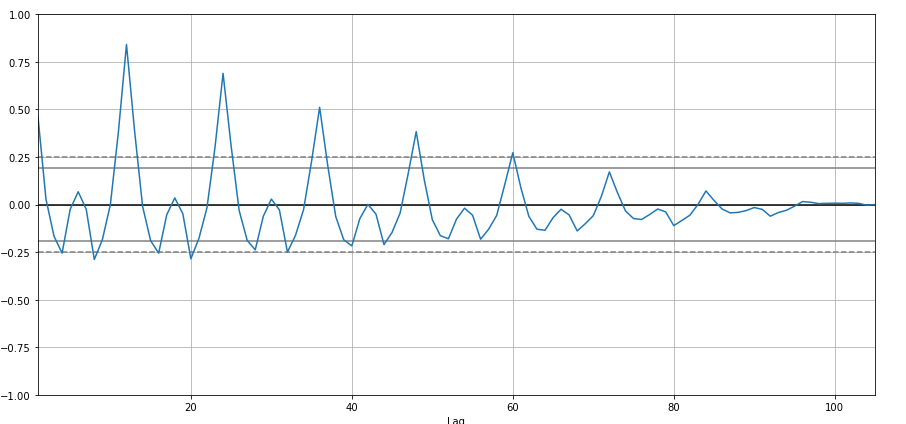
Vou criar autocorrelação:
from pandas.plotting import autocorrelation_plot
autocorrelation_plot(df['Vendas'])
plt.show()
de statsmodels.graphics.tsaplots importação plot_acf,plot_pacf
import statsmodels.api as sm
fig = plt.figure(figsize =(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df['Primeira Diferença Sazonal'].derrubar(),lags=40,ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df['Primeira Diferença Sazonal'].derrubar(),lags=40,ax=ax2)
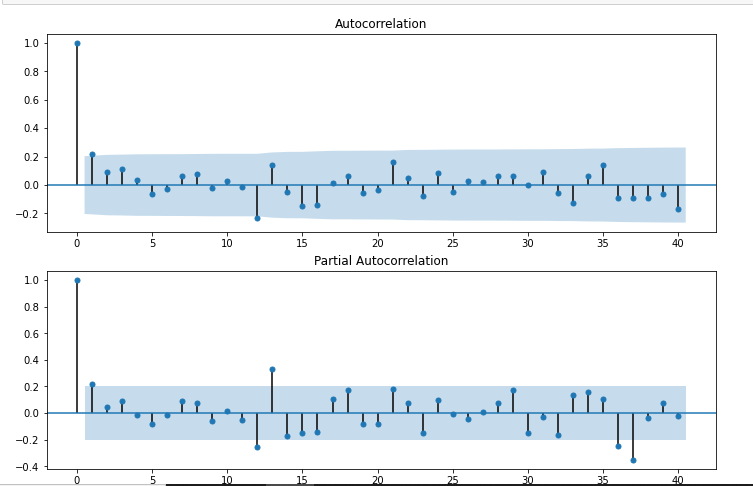
# For non-seasonal data #p=1, d=1, q=0 ou 1 from statsmodels.tsa.arima_model import ARIMA model=ARIMA(df['Vendas'],ordem=(1,1,1)) model_fit=modelo.fit() model_fit.summary()
| Dep. Variável: | D. Vendas | Não. Observações: | 104 |
|---|---|---|---|
| Modelo: | ARIMA (1, 1, 1) | probabilidade logarítmica | -951.126 |
| Método: | css-mle | SD de innovaciones | 2227.262 |
| Encontro: | Rio Mié, 28 outubro 2020 | AIC | 1910.251 |
| Clima: | 11:49:08 | BIC | 1920.829 |
| Shows: | 02-01-1964 | HQIC | 1914.536 |
| – 09-01-1972 |
| Coeficiente | std err | Com | P> | Com | | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| constante | 22.7845 | 12.405 | 1.837 | 0.066 | -1.529 | 47.098 |
| ar. L1. Vendas D | 0.4343 | 0,089 | 4.866 | 0.000 | 0,259 | 0,609 |
| mamã. L1. Vendas D | -1,0000 | 0,026 | -38.503 | 0.000 | -1.051 | -0,949 |
| Verdade | Imaginário | Módulo | Frequência | |
|---|---|---|---|---|
| AR.1 | 2.3023 | + 0,0000j | 2.3023 | 0,0000 |
| MA.1 | 1,0000 | + 0,0000j | 1,0000 | 0,0000 |
df['previsão']=model_fit.predict(start=90,end=103,dynamic=True) df[['Vendas','previsão']].enredo(figsize =(12,8))
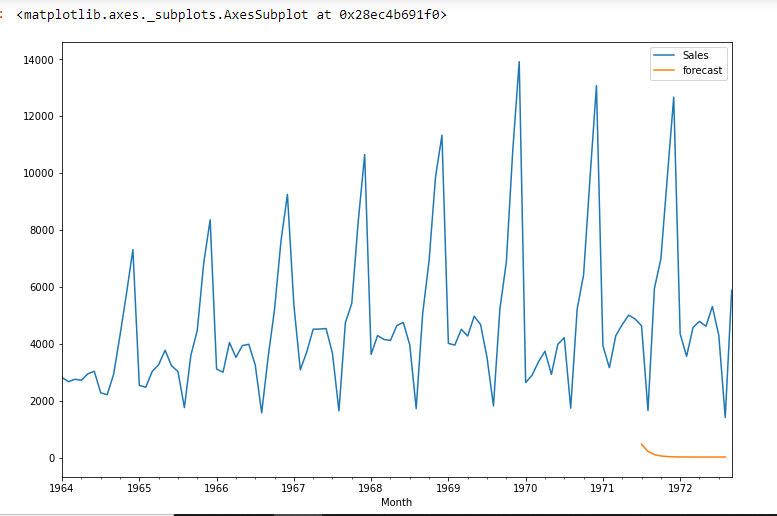
import statsmodels.api as sm
model=sm.tsa.statespace.SARIMAX(df['Vendas'],ordem=(1, 1, 1),seasonal_order=(1,1,1,12))
resultados=modelo.fit()
df['previsão']=resultados.prever(start=90,end=103,dynamic=True)
df[['Vendas','previsão']].enredo(figsize =(12,8))
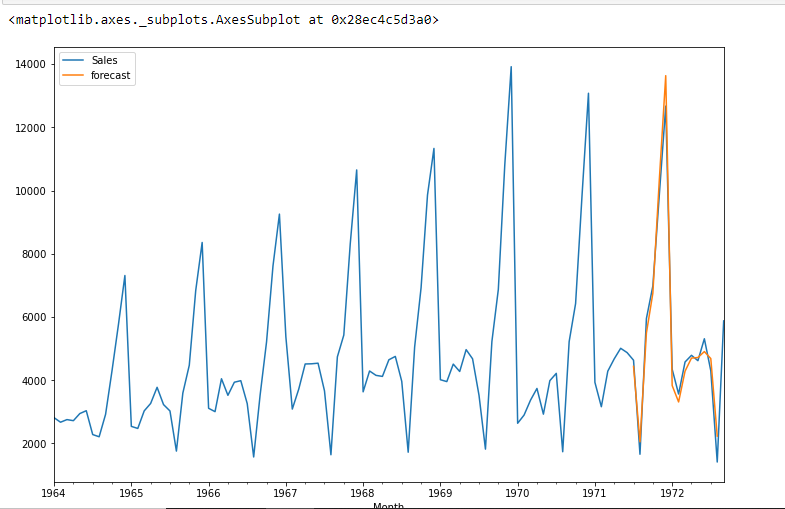
from pandas.tseries.offsets import DateOffset
future_dates=[df.index[-1]+ DateOffset(meses=x)para x no alcance(0,24)]
future_datest_df=pd.DataFrame(future_datest_df=pd.DataFrame[1:],colunas = df.columns)
future_datest_df=pd.DataFrame()
future_datest_df=pd.DataFrame([df,future_datest_df=pd.DataFrame])
future_datest_df=pd.DataFrame['previsão'] future_datest_df=pd.DataFrame(start = 104, future_datest_df=pd.DataFrame 120, future_datest_df=pd.DataFrame)
future_datest_df=pd.DataFrame[['Vendas', 'previsão']].enredo(figsize =(12, 8))
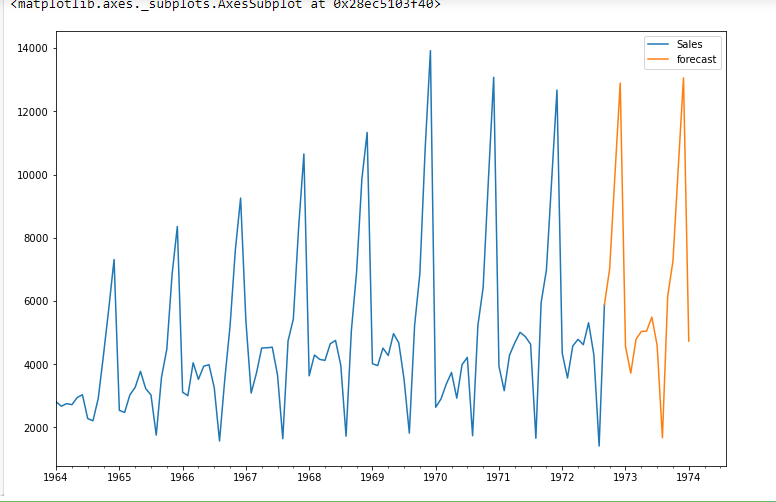
conclusão
A previsão de séries temporais é realmente útil quando temos que tomar decisões futuras ou quando temos que fazer análises, podemos fazer isso rapidamente usando ARIMA, existem muitos outros modelos a partir dos quais podemos fazer previsões de séries temporais, mas ARIMA é realmente fácil de entender.
Espero que este artigo o ajude e economize uma boa quantidade de tempo.. Deixe-me saber se você tem alguma sugestão..
CÓDIGO FELIZ.
Prabhat Pathak (Perfil do linkedIn) future_datest_df=pd.DataFrame.






