Como detectar e eliminar outliers

Este artigo foi publicado como parte do Data Science Blogathon

Introdução

No meu artigo anterior, Eu falo sobre os conceitos teóricos sobre outliers e tento encontrar a resposta para a pergunta: “Quando devemos remover os outliers e quando devemos mantê-los?”.

Para entender melhor este artigo, você deve primeiro ler isso Artigo e, em seguida, prossiga para que você tenha uma ideia clara sobre a análise de outlier em projetos de ciência de dados.

Neste artigo, Tentaremos responder às seguintes questões juntamente com o Piton implementação,

👉 Como lidar com outliers?

👉 Como detectar outliers?

👉 Quais são as técnicas de detecção e remoção de outliers?

Comecemos

Como lidar com outliers?

👉 Guarnição: Excluir outliers. de nossa análise. Aplicando esta técnica, nosso os dados tornam-se escassos quando há mais outliers presentes no conjunto de dados. Sua principal vantagem é o seu O mais rápido natureza.

👉Tamponamento: Nesta técnica, Cap nosso outliers e faça o limite quer dizer, acima ou abaixo de um determinado valor, todos os valores serão considerados outliers, e o número de outliers no conjunto de dados dá esse número limite.

Por exemplo, Se você está trabalhando na função de renda, pessoas acima de um determinado nível de renda podem se comportar da mesma forma que aquelas com renda mais baixa. Neste caso, pode limitar o valor da receita a um nível que o mantenha intacto e, em consequência, lidar com outliers.

👉Trate os outliers como um valor ausente: Por assumindo outliers como observações ausentes, trate-os de acordo, quer dizer, igual a valores ausentes.

Você pode verificar o item de valor ausente aqui

👉 Discretização: Nesta técnica, ao fazer os grupos, incluímos os outliers em um determinado grupo e os forçamos a se comportar da mesma maneira que os de outros pontos desse grupo. Esta técnica também é conhecida como Binning.

Você pode aprender mais sobre discretização aqui.

Como detectar outliers?

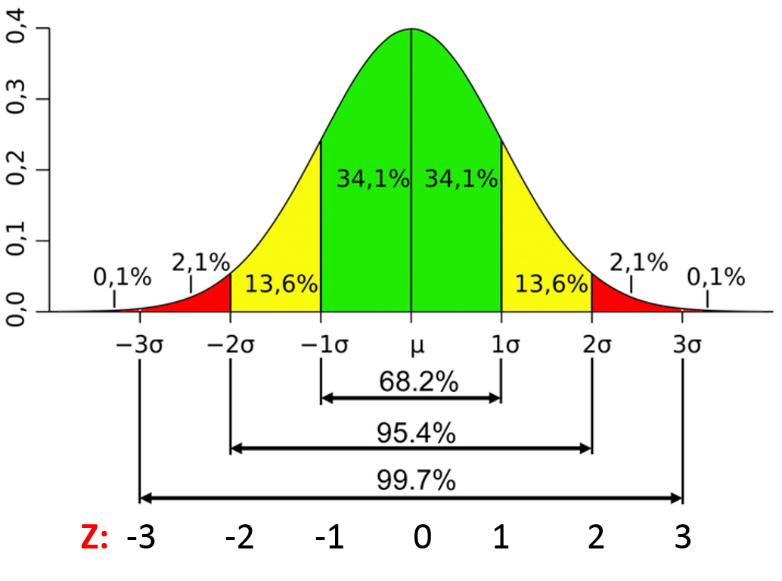
👉 Para distribuições normais: Use relações de distribuição normal empíricas.

– Os pontos de dados abaixo media-3 * (sigma) ou acima meios de comunicação + 3 * (sigma) são outliers.

onde média e sigma são os valor médio e Desvio padrão de uma coluna particular.

FIG. Características de uma distribuição normal

Fonte da imagem: Ligação

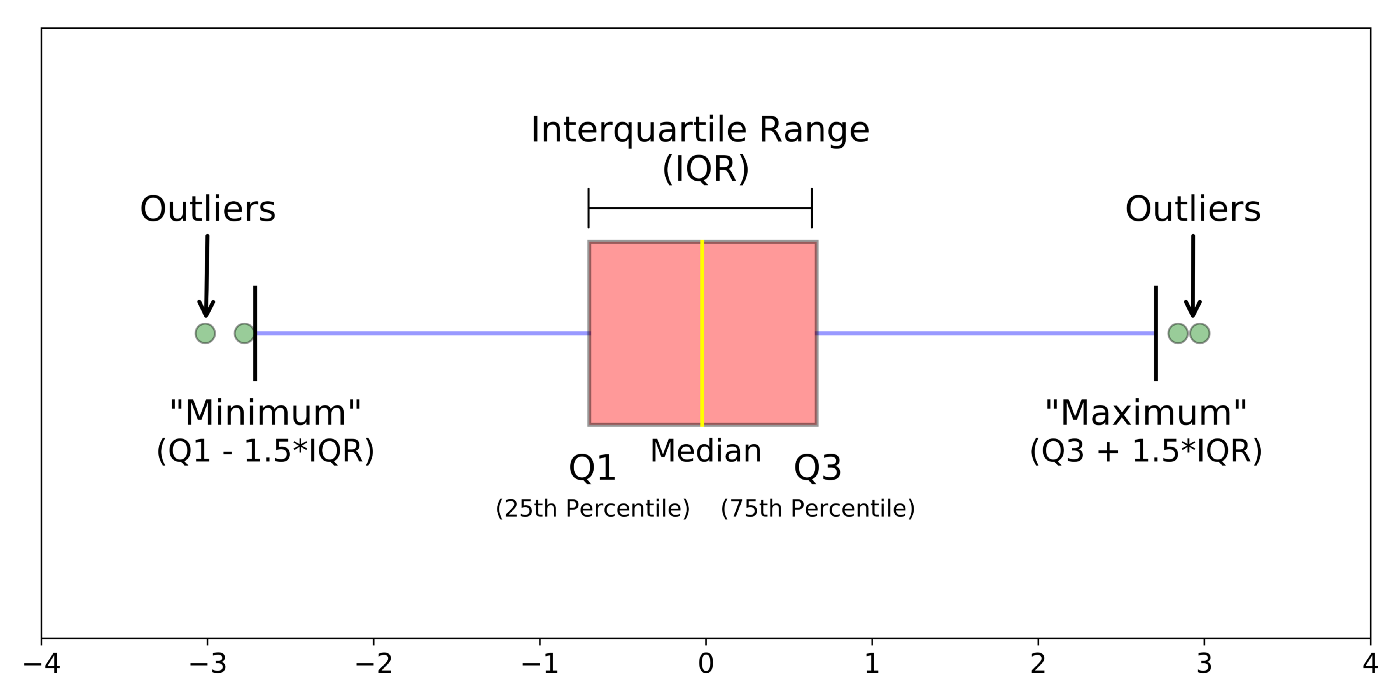
👉 Para distribuições distorcidas: Use a regra de proximidade de intervalo interquartil (IQR).

– Os pontos de dados abaixo T1 – 1.5 IQR ou acima 3º T + 1.5 IQR são outliers.

onde Q1 e Q3 são os 25 e Percentil 75 do conjunto de dados respectivamente, e IQR representa o intervalo interquartil e é dado por Q3 – T1.

FIG. IQR para detectar outliers

Fonte da imagem: Ligação

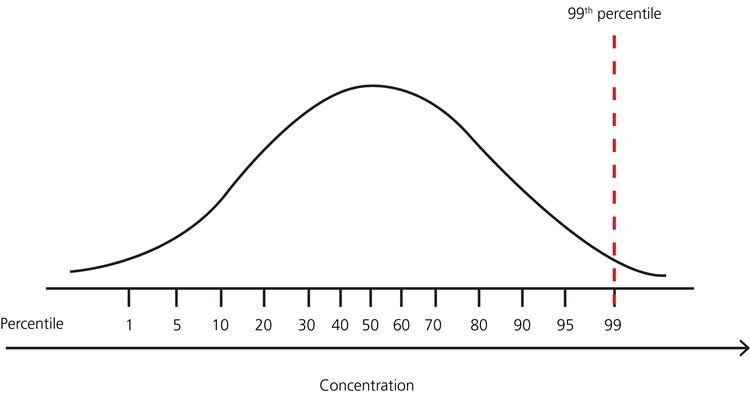
👉 Para outras distribuições: Usar abordagem baseada em percentil.

Por exemplo, Pontos de dados que estão longe do percentil 99% e menos do que o percentil 1 são considerados outliers.

FIG. Representação de percentil

Fonte da imagem: Ligação

Técnicas para detecção e eliminação de outliers:

👉 Tratamento de pontuação Z:

Suposição– Os recursos são normalmente ou aproximadamente normalmente distribuídos.

Paso 1: Importação de dependências necessárias

importar numpy como np
importar pandas como pd
import matplotlib.pyplot as plt
importado do mar como sns

Paso 2: leia e carregue o conjunto de dados

df = pd.read_csv('placement.csv')
df.sample(5)

Paso 3: Plote os lotes de distribuição para os recursos

import warnings
warnings.filterwarnings('ignorar')
plt.figure(figsize =(16,5))
plt.subplot(1,2,1)
sns.distplot(df['cgpa'])
plt.subplot(1,2,2)
sns.distplot(df['placement_exam_marks'])
plt.show()

Paso 4: encontrar os valores-limite

imprimir("Maior permitida",df['cgpa'].quer dizer() + 3*df['cgpa'].std())
imprimir("Menor permitida",df['cgpa'].quer dizer() - 3*df['cgpa'].std())

Produção:

Maior permitida 8.808933625397177
Menor permitida 5.113546374602842

Paso 5: descobrir outliers

df[(df['cgpa'] > 8.80) | (df['cgpa'] < 5.11)]

Paso 6: Aparador outlier

new_df = df[(df['cgpa'] < 8.80) & (df['cgpa'] > 5.11)]
new_df

Paso 7: limitação outlier

upper_limit = df['cgpa'].quer dizer() + 3*df['cgpa'].std()
lower_limit = df['cgpa'].quer dizer() - 3*df['cgpa'].std()

Paso 8: agora, aplicar a tampa

df['cgpa'] = np.where(
    df['cgpa']>upper_limit,
    upper_limit,
    np.where(
        df['cgpa']<lower_limit,
        lower_limit,
        df['cgpa']
    )
)

Paso 9: agora ver as estatísticas usando o “Descrever”

df['cgpa'].descrever()

Produção:

contar    1000.000000
quer dizer        6.961499
std         0.612688
min         5.113546
25%         6.550000
50%         6.960000
75%         7.370000
max         8.808934
Nome: cgpa, tipo d: float64

Isso completa nossa técnica baseada em pontuação Z!!

👉 Filtragem baseada em IQR:

Usado quando nossa distribuição de dados é tendenciosa.

Paso 1: importar as dependências necessárias

importar numpy como np
importar pandas como pd
import matplotlib.pyplot as plt
importado do mar como sns

Paso 2: leia e carregue o conjunto de dados

df = pd.read_csv('placement.csv')
df.head()

Paso 3: Plote o gráfico de distribuição dos recursos.

plt.figure(figsize =(16,5))
plt.subplot(1,2,1)
sns.distplot(df['cgpa'])
plt.subplot(1,2,2)
sns.distplot(df['placement_exam_marks'])
plt.show()

Paso 4: Forme um diagrama de caixa para o recurso tendencioso

sns.boxplot(df['placement_exam_marks'])

Paso 5: Encontre o IQR

percentil25 = df['placement_exam_marks'].Quântico(0.25)
percentil75 = df['placement_exam_marks'].Quântico(0.75)

Paso 6: Encontre o limite superior e inferior

upper_limit = percentil75 + 1.5 * iqr
lower_limit = percentile25 - 1.5 * Iqr

Paso 7: descobrir outliers

df[df['placement_exam_marks'] > upper_limit]
df[df['placement_exam_marks'] < lower_limit]

Paso 8: Cortar fora

new_df = df[df['placement_exam_marks'] < upper_limit]
new_df.forma

Paso 9: Compare parcelas após o corte

plt.figure(figsize =(16,8))
plt.subplot(2,2,1)
sns.distplot(df['placement_exam_marks'])
plt.subplot(2,2,2)
sns.boxplot(df['placement_exam_marks'])
plt.subplot(2,2,3)
sns.distplot(new_df['placement_exam_marks'])
plt.subplot(2,2,4)
sns.boxplot(new_df['placement_exam_marks'])
plt.show()

Paso 10: Ligado

new_df_cap = df.copy()
new_df_cap['placement_exam_marks'] = np.where(
    new_df_cap['placement_exam_marks'] > upper_limit,
    upper_limit,
    np.where(
        new_df_cap['placement_exam_marks'] < lower_limit,
        lower_limit,
        new_df_cap['placement_exam_marks']
    )
)

Paso 11: Compare parcelas após limitação

plt.figure(figsize =(16,8))
plt.subplot(2,2,1)
sns.distplot(df['placement_exam_marks'])
plt.subplot(2,2,2)
sns.boxplot(df['placement_exam_marks'])
plt.subplot(2,2,3)
sns.distplot(new_df_cap['placement_exam_marks'])
plt.subplot(2,2,4)
sns.boxplot(new_df_cap['placement_exam_marks'])
plt.show()

Isso completa nossa técnica baseada em IQR!

👉 Percentil:

– Esta técnica funciona definindo um determinado valor de limiar, que decide com base em nossa abordagem para o problema.

– Enquanto eliminamos outliers limitando, esse método particular é conhecido como Winsorización.

– Aqui a gente sempre guarda simetria em ambos os lados significa que se removermos o 1% direito, então, à esquerda, também diminuímos um 1%.

Paso 1: importar as dependências necessárias

importar numpy como np
importar pandas como pd

Paso 2: leia e carregue o conjunto de dados

df = pd.read_csv('peso-altura.csv')
df.sample(5)

Paso 3: Esboce o gráfico de distribuição das características de “altura”

sns.distplot(df['Altura'])

Paso 4: Esboce o box plot da característica de “altura”

sns.boxplot(df['Altura'])

Paso 5: Encontre o limite superior e inferior

upper_limit = df['Altura'].Quântico(0.99)
lower_limit = df['Altura'].Quântico(0.01)

Paso 7: aplicar acabamento

new_df = df[(df['Altura'] <= 74.78) & (df['Altura'] >= 58.13)]

Paso 8: Compare a distribuição e o gráfico de caixa após o recorte

sns.distplot(new_df['Altura'])
sns.boxplot(new_df['Altura'])

👉 Winsorización:

Paso 9: Aplicar limitação (Winsorización)

df['Altura'] = np.where(df['Altura'] >= Upper_limit,
        upper_limit,
        np.where(df['Altura'] <= lower_limit,
        lower_limit,
        df['Altura']))

Paso 10: Compare a distribuição e o gráfico de caixa após a restrição

sns.distplot(df['Altura'])
sns.boxplot(df['Altura'])

Isso completa nossa técnica baseada em percentil!!

Notas finais

Obrigado pela leitura!

Se você gostou e quer saber mais, visite meus outros artigos sobre ciência de dados e aprendizado de máquina clicando no Ligação

Sinta-se à vontade para entrar em contato comigo em Linkedin, Correio eletrônico.

Qualquer coisa não mencionada ou você deseja compartilhar suas idéias? Sinta-se à vontade para comentar abaixo e eu entrarei em contato com você.

Sobre o autor

Chirag Goyal

Atualmente, Estou cursando bacharelado em tecnologia (B.Tech) em Ciência da Computação e Engenharia da Instituto Indiano de Tecnologia de Jodhpur (IITJ). Estou muito animado com o aprendizado de máquina, a aprendizado profundoAqui está o caminho de aprendizado para dominar o aprendizado profundo em, Uma subdisciplina da inteligência artificial, depende de redes neurais artificiais para analisar e processar grandes volumes de dados. Essa técnica permite que as máquinas aprendam padrões e executem tarefas complexas, como reconhecimento de fala e visão computacional. Sua capacidade de melhorar continuamente à medida que mais dados são fornecidos a ele o torna uma ferramenta fundamental em vários setores, da saúde... e inteligência artificial.

A mídia mostrada neste artigo não é propriedade da DataPeaker e é usada a critério do autor.

Relacionado