Este artigo foi publicado como parte do Data Science Blogathon.
Introdução
Vou discutir este tópico em detalhes abaixo.
Etapas de regressão linear
Como o nome sugere, a ideia por trás da realização da regressão linear é que devemos chegar a uma equação linear que descreve a relação entre variáveis dependentes e independentes..
Paso 1
Supongamos que tenemos un conjunto de datos donde x es la variávelEm estatística e matemática, uma "variável" é um símbolo que representa um valor que pode mudar ou variar. Existem diferentes tipos de variáveis, e qualitativo, que descrevem características não numéricas, e quantitativo, representando quantidades numéricas. Variáveis são fundamentais em experimentos e estudos, uma vez que permitem a análise de relações e padrões entre diferentes elementos, facilitando a compreensão de fenômenos complexos.... independiente e Y es una función de x (E= f (x)). Portanto, usando regressão linear podemos formar a seguinte equação (equação para a linha mais adequada):
Y = mx + c
Esta é uma equação de uma linha reta onde m é a inclinação da linha e c é a intersecção.
Paso 2
Agora, para derivar a linha mais adequada, primeiro atribuímos valores aleatórios à minha senhora, calculamos o valor correspondente de Y para um dado x. este valor y é o valor de saída.
Paso 3
Como a regressão logística é um algoritmo supervisionado de aprendizagem de máquina, já sabemos o valor de Y real (variável dependente). Agora, como temos nosso valor de saída calculado (vamos representá-lo como ŷ), podemos verificar se nossa previsão é precisa ou não.
No caso da regressão linear, calculamos esse erro (residual) usando o método MSE (erro quadrático médio) y lo denominamos Função de perdaA função de perda é uma ferramenta fundamental no aprendizado de máquina que quantifica a discrepância entre as previsões do modelo e os valores reais. Seu objetivo é orientar o processo de treinamento, minimizando essa diferença, permitindo assim que o modelo aprenda de forma mais eficaz. Existem diferentes tipos de funções de perda, como erro quadrático médio e entropia cruzada, cada um adequado para diferentes tarefas e...:
A função de perda pode ser escrita como:
L = 1 / n ∑ ((e – ŷ)2)
Onde n é o número de observações.
Paso 4
Para alcançar a melhor linha ajustada, temos que minimizar o valor da função de perda.
Para minimizar a função de perda, utilizamos una técnica llamada descenso de gradienteGradiente é um termo usado em vários campos, como matemática e ciência da computação, descrever uma variação contínua de valores. Na matemática, refere-se à taxa de variação de uma função, enquanto em design gráfico, Aplica-se à transição de cores. Esse conceito é essencial para entender fenômenos como otimização em algoritmos e representação visual de dados, permitindo uma melhor interpretação e análise em....
Vamos analisar como funciona a descida gradiente (embora eu não vou mergulhar nos detalhes, como este não é o tema central deste artigo).
Gradiente descendente
Se olharmos para a fórmula da função de perda, o 'erro quadrado médio'’ significa que o erro é representado em termos de segunda ordem.
Se fizermos um gráfico da função de perda para o peso (em nossa equação os pesos são myc), será uma curva parabólica. Agora que nossa moto é para minimizar a função de perda, temos que chegar ao fim da curva.
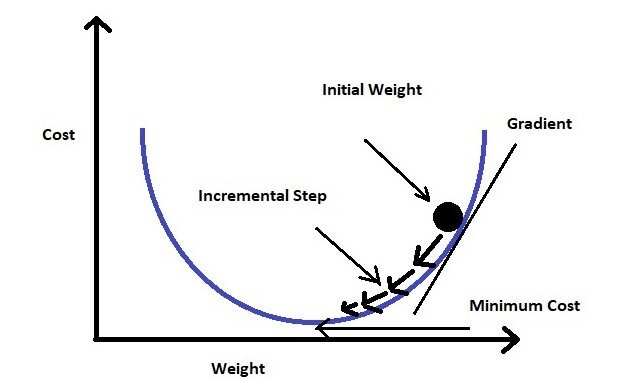
Para alcançar isto, devemos tomar a derivada de primeira ordem da função de perda para pesos (Myc). Então vamos subtrair o resultado da derivada do peso inicial multiplicando-se por uma taxa de aprendizagem (uma). Continuaremos repetindo esta etapa até chegarmos ao valor mínimo (chamamos de mínimos globais). Nós estabelecemos um limiar de um valor muito pequeno (exemplo: 0.0001) como mínimos globais. Se não definirmos o valor limite, pode levar uma eternidade para alcançar o valor zero exato.
Paso 5
Uma vez que a função de perda é minimizada, temos a equação final para a linha mais adequada e podemos prever o valor de Y para qualquer X dado.
É aí que termina a regressão linear e estamos a um passo de alcançar a regressão logística..
Regressão logística
Como eu disse antes, fundamentalmente, regressão logística é usado para classificar elementos de um conjunto em dois grupos (classificação binária) calculando a probabilidade de cada elemento do conjunto.
Etapas de regressão logística
Na regressão logística, decidimos sobre um limiar de probabilidade. Se a probabilidade de um determinado elemento for maior do que o limiar de probabilidade, classificamos esse elemento em um grupo ou vice-versa.
Paso 1
Para calcular a separação binária, primeiro, determinamos a melhor linha ajustada seguindo os passos da Regressão Linear.
Paso 2
A linha de regressão que oremos da regressão linear é muito suscetível a outliers.. Portanto, não vai fazer um bom trabalho de classificar duas classes.
Portanto, o valor previsto é convertido em probabilidade, alimentando-o para a função sigmoid.
A equação sigmoide:

Como podemos ver no Fig. 3, podemos alimentar qualquer número real para a função sigmoid e ele vai retornar um valor entre 0 e 1.
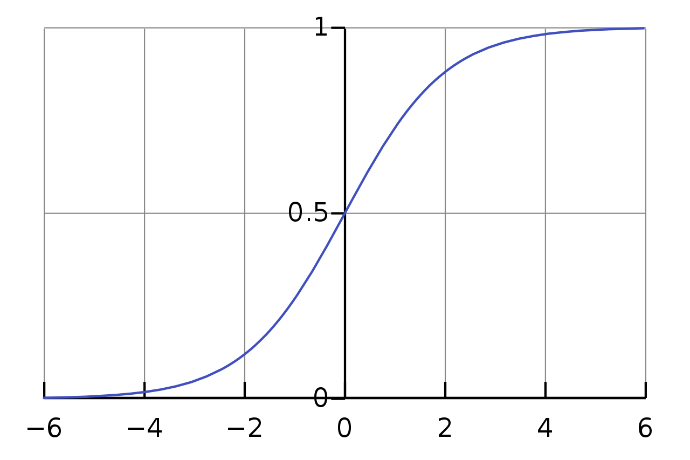
FIG 2: Curva sigmoide (imagem tirada da Wikipédia)
Portanto, se alimentarmos a saída ŷ valor para função sigmoid retunes um valor de probabilidade entre 0 e 1.
Paso 3
Finalmente, o valor de saída da função sigmoid torna-se 0 o 1 (valores discretos) de acordo com o valor limiar. Em geral, definimos o valor limiar para 0,5. Desta forma, temos a classificação binária.
Agora que temos a ideia básica de como a regressão linear e a regressão logística estão relacionadas., vamos rever o processo com um exemplo.
Exemplo
Considere um problema onde somos fornecidos com um conjunto de dados que contém a altura e o peso de um grupo de pessoas.. Nossa tarefa é prever o Peso para novas entradas na coluna Altura.
Então podemos descobrir que este é um problema de regressão no qual construiremos um modelo de regressão linear.. Vamos treinar o modelo com os valores de altura e peso fornecidos. Uma vez que o modelo é treinado, podemos prever o peso para um dado valor de altura desconhecido.
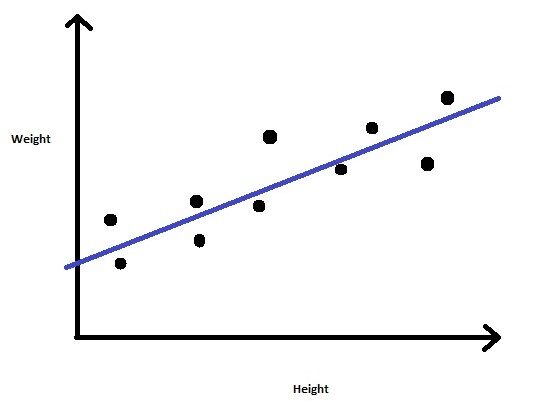
FIG 3: Regressão linear
Agora suponha que temos um campo adicional Obesidade e temos que classificar se uma pessoa é obesa ou não com base em sua altura e peso proporcionais. Este é claramente um problema de classificação onde temos que segregar o conjunto de dados em duas classes. (obesos e não obesos).
Então, para o novo problema, podemos novamente seguir os passos da Regressão Linear e construir uma linha de regressão. Desta vez, la línea se basará en dos parametroso "parametros" são variáveis ou critérios usados para definir, medir ou avaliar um fenômeno ou sistema. Em vários domínios, como a estatística, Ciência da Computação e Pesquisa Científica, Os parâmetros são essenciais para estabelecer normas e padrões que orientam a análise e interpretação dos dados. Sua seleção e manuseio adequados são cruciais para obter resultados precisos e relevantes em qualquer estudo ou projeto.... Altura y Peso y la línea de regresión se ajustará entre dos conjuntos de valores discretos. Como esta linha de regressão é muito suscetível a outliers, não servirá para classificar duas classes.
Para uma classificação melhor, vamos alimentar os valores de saída da linha de regressão para a função sigmoide. a função sigmoid retorna a probabilidade de cada valor de saída da linha de regressão. Agora, com base em um valor limiar predefinido, podemos facilmente classificar a saída em duas classes de obesos ou não-obesos.
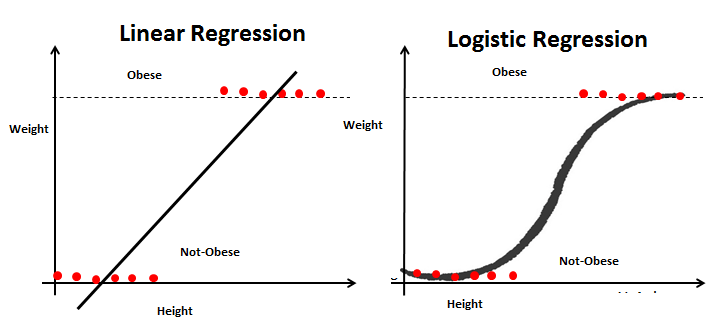
Finalmente, podemos resumir as semelhanças e diferenças entre esses dois modelos.
As semelhanças entre regressão linear e regressão logística
- Tanto a regressão linear quanto a regressão logística são algoritmos supervisionados de aprendizagem de máquina..
- Regressão linear e regressão logística, ambos os modelos são regressão paramétrica, quer dizer, ambos os modelos usam equações lineares para previsões.
Essas são todas as semelhanças que temos entre esses dois modelos..
Porém, em termos de funcionalidade, esses dois são completamente diferentes. Abaixo estão as diferenças.
As diferenças entre regressão linear e regressão logística
- Regressão linear é usada para lidar com problemas de regressão, enquanto a regressão logística é usada para lidar com problemas de classificação.
- A regressão linear proporciona saída contínua, mas a regressão logística proporciona uma produção discreta.
- O objetivo da regressão linear é encontrar a linha mais adequada., enquanto a regressão logística está um passo à frente e ajusta os valores da linha para a curva sigmoid.
- O método para calcular a função de perda na regressão linear é o erro quadrado médio, enquanto para regressão logística é a estimativa de máxima probabilidade.
Observação: No momento da redação deste artigo, Presumi que o leitor já está familiarizado com o conceito básico de regressão linear e regressão logística. Espero que este artigo explique a relação entre esses dois conceitos.






